Divide and Conquer

1. Giới thiệu về thuật toán chia để trị

1.1 Định nghĩa của thuật toán chia để trị

Thuật toán chia để trị (Divide and Conquer): Ý nghĩa đen là “chia và giải quyết”, nghĩa là chia một vấn đề phức tạp thành hai hoặc nhiều vấn đề con giống nhau hoặc tương tự, cho đến khi cuối cùng các vấn đề con có thể được giải quyết một cách đơn giản và trực tiếp, kết quả của vấn đề gốc là tổng hợp của các giải pháp của các vấn đề con.

Đơn giản mà nói, ý tưởng cơ bản của thuật toán chia để trị là: chia nhỏ vấn đề lớn thành các vấn đề con, giảm kích thước vấn đề cho đến khi có thể giải trực tiếp.

1.2 Sự khác biệt và sự tương đồng giữa thuật toán chia để trị và thuật toán đệ quy

Về mặt định nghĩa, ý tưởng của thuật toán chia để trị và thuật toán đệ quy là giống nhau, đều là chia nhỏ vấn đề lớn thành các vấn đề con.

Thực tế, mối quan hệ giữa thuật toán chia để trị và thuật toán đệ quy là một mối quan hệ chứa và được chứa, có thể coi là: Thuật toán đệ quy ∈ Thuật toán chia để trị.

Cách triển khai thuật toán chia để trị có thể được chia thành hai loại: “Thuật toán đệ quy” và “Thuật toán lặp”.

Trong đó, thuật toán chia để trị thường được triển khai bằng thuật toán đệ quy. Tuy nhiên, ngoài thuật toán đệ quy, thuật toán chia để trị cũng có thể được triển khai bằng thuật toán lặp. Một số ví dụ phổ biến bao gồm: thuật toán biến đổi Fourier nhanh, thuật toán tìm kiếm nhị phân, thuật toán sắp xếp trộn không đệ quy, v.v.

1.3 Điều kiện áp dụng của thuật toán chia để trị

Thuật toán chia để trị có thể giải quyết các vấn đề khi thoả mãn $4$ điều kiện sau:

Vấn đề gốc có thể chia thành nhiều vấn đề con cùng dạng và kích thước nhỏ hơn.
Các vấn đề con chia nhỏ có thể được giải quyết độc lập, tức là không có vấn đề con chung.
Có điều kiện dừng chia nhỏ, tức là khi kích thước vấn đề đủ nhỏ, có thể giải trực tiếp bằng phương pháp đơn giản.
Kết quả của các vấn đề con có thể được kết hợp để tạo thành kết quả của vấn đề gốc, và thao tác kết hợp không quá phức tạp, nếu không sẽ không giảm được độ phức tạp tổng thể của thuật toán.

2. Các bước cơ bản của thuật toán chia để trị

Việc giải quyết vấn đề bằng thuật toán chia để trị chủ yếu bao gồm $3$ bước:

Chia nhỏ: Chia vấn đề cần giải quyết thành các vấn đề con cùng dạng và tương tự.
Giải quyết: Đệ quy giải quyết từng vấn đề con.
Kết hợp: Dựa trên yêu cầu của vấn đề gốc, kết hợp các kết quả của các vấn đề con để tạo thành kết quả của vấn đề gốc.

Trong đó, trong bước $1$ , việc chia nhỏ vấn đề thành các vấn đề con nên được thực hiện sao cho các vấn đề con có kích thước tương đương. Nói cách khác, chia vấn đề thành $k$ vấn đề con cùng kích thước là một phương pháp hiệu quả để cân bằng các vấn đề con. Trong nhiều vấn đề, có thể lấy $k = 2$ . Phương pháp này để cân bằng các vấn đề con gần như luôn tốt hơn so với việc chia vấn đề thành các vấn đề con không cân bằng.

Sau khi hoàn thành bước $2$ , giải quyết các vấn đề con nhỏ nhất, kết quả của vấn đề nhỏ nhất có thể được tính toán trong thời gian thực hiện hằng số. Sau đó, chúng ta tiến hành kết hợp các giải pháp của các vấn đề con theo thứ tự của quá trình đệ quy từ dưới lên, tạo thành kết quả của vấn đề gốc.

Khi triển khai thuật toán chia để trị, chúng ta cũng tuân thủ $3$ bước trên để viết mã, tương ứng với mã giả như sau:

def divide_and_conquer(problem):                # problem là kích thước của vấn đề
    if problem < d:                             # Khi kích thước vấn đề đủ nhỏ, giải quyết trực tiếp vấn đề này
        return solove();                        # Giải quyết trực tiếp
    
    k_problems = divide(problem)                # Chia vấn đề thành k vấn đề con cùng dạng
    
    res = [0 for _ in range(k)]                 # res để lưu trữ kết quả của k vấn đề con
    for k_problem in k_problems:
        res[i] = divide_and_conquer(k_problem)  # Đệ quy giải quyết k vấn đề con
    
    ans = merge(res)                            # Kết hợp kết quả của k vấn đề con
    return ans                                  # Trả về kết quả của vấn đề gốc

3. Phân tích độ phức tạp của thuật toán chia để trị

Trong thuật toán chia để trị, sau khi tiếp tục đệ quy, các vấn đề con cuối cùng sẽ trở nên rất đơn giản và có thể giải quyết trong thời gian thực hiện hằng số. Do đó, độ phức tạp thời gian do thuật toán chia để trị gây ra trong toàn bộ quá trình thực hiện là rất nhỏ và có thể bỏ qua. Vì vậy, độ phức tạp thời gian của thuật toán chia để trị thực tế là do hai phần “phân rã” và “kết hợp” tạo thành.

Nhìn chung, thuật toán chia để trị chia một vấn đề thành a vấn đề con cùng cấu trúc, mỗi vấn đề con có kích thước là n / b, sau đó thời gian phân rã tổng quát có thể biểu diễn bằng biểu thức đệ quy sau:

$T(n) = \begin{cases} \begin{array} \ \Theta{(1)} & n = 1 \cr a * T(n/b) + f(n) & n > 1 \end{array} \end{cases}$

Trong đó, số vấn đề con được tạo ra mỗi lần phân rã là a, kích thước của mỗi vấn đề con là 1 / b của kích thước vấn đề gốc, thời gian phân rã và kết hợp a vấn đề con là f(n).

Vì vậy, để tính toán độ phức tạp thời gian của một thuật toán chia để trị, chúng ta cần giải quyết biểu thức đệ quy trên. Có nhiều phương pháp để giải quyết biểu thức đệ quy, ở đây chúng tôi giới thiệu hai phương pháp phổ biến là “phương pháp đệ quy” và “phương pháp cây đệ quy”.

3.1 Phương pháp đệ quy

Dựa trên biểu thức đệ quy của vấn đề, chúng ta có thể suy ra kết quả cuối cùng bằng cách phân tích từng bước phân rã.

Ví dụ với thuật toán sắp xếp trộn, chúng ta sẽ tính toán độ phức tạp thời gian bằng phương pháp đệ quy.

Biểu thức đệ quy của thuật toán sắp xếp trộn như sau:

$T(n) = \begin{cases} \begin{array} \ O{(1)} & n = 1 \cr 2T(n/2) + O(n) & n > 1 \end{array} \end{cases}$

Dựa trên biểu thức đệ quy của thuật toán sắp xếp trộn, khi n > 1, chúng ta có thể tính toán theo cách sau:

$T (n) = 2 T (n /2) + O (n) = 2 (2 T (n /4) + O (n /2)) + O (n) = 4 T (n /4) + 2 O (n) = 8 T (n /8) + 3 O (n) = \dots\dots = 2^{x} \times T (n / 2^{x}) + x \times O (n)$

Khi phân tích đệ quy đạt đến kích thước cuối cùng là 1, giả sử n = 2^x, ta có x = log_2n, từ đó:

$\begin{align} T(n) & = n \times T(1) + \log_2n \times O(n) \cr & = n + \log_2n \times O(n) \cr & = O(n \times \log_2n) \end{align}$

Vậy độ phức tạp thời gian của thuật toán sắp xếp trộn là $O (n \times lo g_{2} n)$ .

3.2 Phương pháp cây đệ quy

Phương pháp cây đệ quy cũng tương tự như phương pháp đệ quy, nhưng cây đệ quy có thể hiển thị rõ ràng và trực quan hơn, cho thấy các nút phân rã và chi phí thời gian tại mỗi tầng.

Công thức tính độ phức tạp thời gian bằng phương pháp cây đệ quy là:

$Đ ộ phức tạp thời gian = S \overset{ˊ}{\overset{o}{ˆ}} l \overset{a}{ˊ} \times T (1) + Tổng chi ph \overset{ı}{ˊ} = 2^{x} \times T (1) + x \times O (n)$ .

Chúng ta vẫn lấy ví dụ với thuật toán sắp xếp trộn và tính toán độ phức tạp thời gian bằng phương pháp cây đệ quy.

Biểu thức đệ quy của thuật toán sắp xếp trộn như sau:

$T(n) = \begin{cases} \begin{array} \ O{(1)} & n = 1 \cr 2T(n/2) + O(n) & n > 1 \end{array} \end{cases}$

Cây đệ quy tương ứng với thuật toán sắp xếp trộn như hình dưới đây.

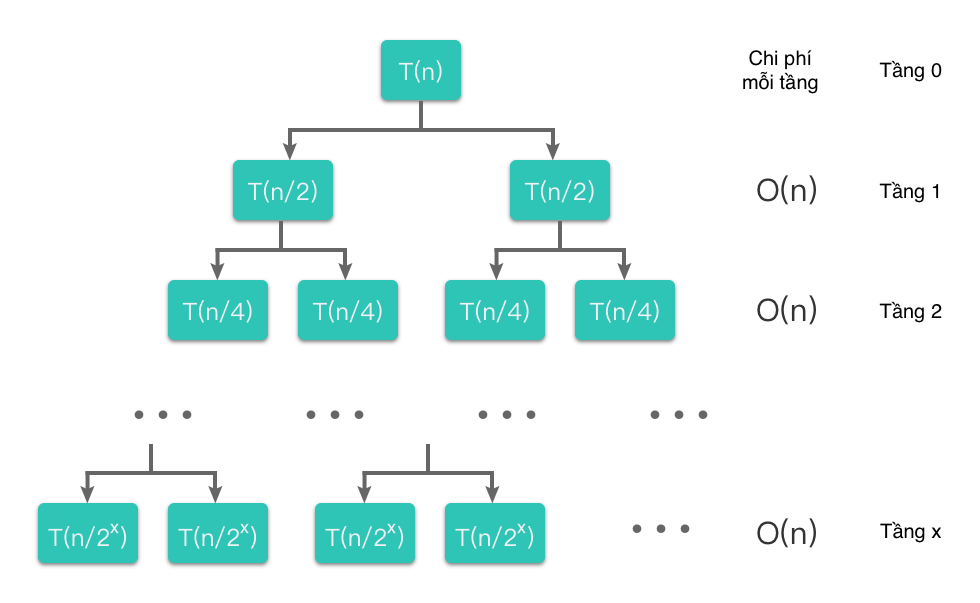
Vì $n = 2^{x}$ , ta có $x = l o g_{2} n$ , từ đó độ phức tạp thời gian của thuật toán sắp xếp trộn là: $2^{x} \times T (1) + x \times O (n) = n + lo g_{2} n \times O (n) = O (n \times l o g_{2} n)$ .

4. Ứng dụng của thuật toán chia để trị

4.1 Sắp xếp trộn (Merge Sort)

4.1.1 Liên kết đề bài

912. Sort an Array

4.1.2 Tóm tắt đề bài

Mô tả: Cho một mảng số nguyên nums.

Yêu cầu: Sắp xếp mảng này theo thứ tự tăng dần.

Giới hạn:

$1 \leq nums.length \leq 5 * 1 0^{4}$ .
$- 5 * 1 0^{4} \leq nums[i] \leq 5 * 1 0^{4}$ .

Ví dụ:

Input: nums = [5,2,3,1]
Output: [1,2,3,5]

4.1.3 Ý tưởng giải quyết

Chúng ta sử dụng thuật toán sắp xếp trộn để giải quyết bài toán này.

Phân rã: Chia dãy số cần sắp xếp thành hai dãy con, mỗi dãy con chứa $\frac{n}{2}$ phần tử.
Giải quyết: Đệ quy sắp xếp và phân rã các dãy con cho đến khi mỗi dãy con chỉ còn một phần tử.
Kết hợp: Trộn hai dãy con đã sắp xếp để tạo ra dãy con mới đã sắp xếp.

4.1.4 Code

class Solution:
    def merge(self, left_arr, right_arr):           # Hợp nhất
        arr = []
        while left_arr and right_arr:               # Chèn các phần tử nhỏ hơn từ hai mảng đã sắp xếp vào mảng kết quả
            if left_arr[0] <= right_arr[0]:
                arr.append(left_arr.pop(0))
            else:
                arr.append(right_arr.pop(0))
                
        while left_arr:                             # Nếu còn phần tử trong mảng con trái, chèn chúng vào mảng kết quả
            arr.append(left_arr.pop(0))
        while right_arr:                            # Nếu còn phần tử trong mảng con phải, chèn chúng vào mảng kết quả
            arr.append(right_arr.pop(0))
        return arr                                  # Trả về mảng đã sắp xếp
 
    def mergeSort(self, arr):                       # Phân rã
        if len(arr) <= 1:                           # Nếu số phần tử trong mảng nhỏ hơn hoặc bằng 1, trả về mảng ban đầu
            return arr
        
        mid = len(arr) // 2                         # Chia mảng thành hai mảng con
        left_arr = self.mergeSort(arr[0: mid])      # Đệ quy sắp xếp và phân rã mảng con trái
        right_arr =  self.mergeSort(arr[mid:])      # Đệ quy sắp xếp và phân rã mảng con phải
        return self.merge(left_arr, right_arr)      # Hợp nhất hai mảng con đã sắp xếp
 
    def sortArray(self, nums: List[int]) -> List[int]:
        return self.mergeSort(nums)

4.2 Tìm kiếm nhị phân

4.2.1 Liên kết đề bài

704. Tìm kiếm nhị phân - LeetCode

4.2.2 Tóm tắt đề bài

Mô tả: Cho một mảng số nguyên nums đã được sắp xếp theo thứ tự tăng dần và một giá trị mục tiêu target.

Yêu cầu: Trả về vị trí của target trong mảng nums, nếu không tìm thấy thì trả về -1.

Giới hạn:

Giả sử mảng nums không chứa các phần tử trùng lặp.
Kích thước của mảng nums nằm trong khoảng từ 1 đến 10000.
$- 9999 \leq nums[i] \leq 9999$ .

Ví dụ:

Input: nums = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: Số 9 xuất hiện trong mảng nums và có chỉ số là 4.

4.2.3 Ý tưởng giải quyết

Chúng ta sử dụng thuật toán chia để trị để giải quyết bài toán này. Khác với các bài toán chia để trị khác, tìm kiếm nhị phân không có quá trình kết hợp, giải pháp của vấn đề con nhỏ nhất chính là giải pháp của vấn đề gốc.

Phân rã: Chia mảng gồm $n$ phần tử thành hai mảng con, mỗi mảng con chứa $\frac{n}{2}$ phần tử.
Giải quyết: So sánh phần tử ở giữa nums[mid] với target.
1. Nếu bằng nhau, trả về vị trí đó.
2. Nếu nums[mid] < target, đệ quy tìm kiếm nhị phân trong mảng con trái.
3. Nếu nums[mid] > target, đệ quy tìm kiếm nhị phân trong mảng con phải.

Quá trình tìm kiếm nhị phân bằng thuật toán chia để trị được mô tả trong hình dưới đây.

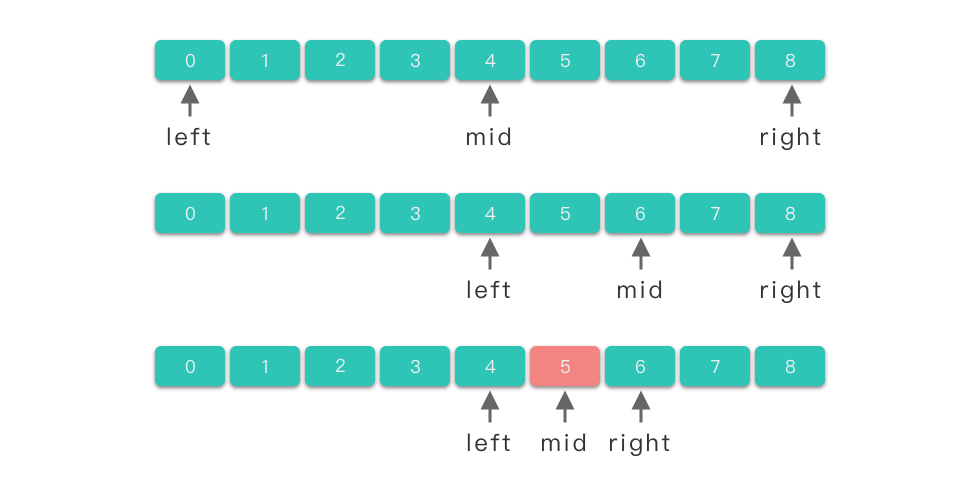
4.2.4 Code

Code của thuật toán chia để trị để tìm kiếm nhị phân (phiên bản không đệ quy) như sau:

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left = 0
        right = len(nums) - 1
        # Tìm kiếm target trong khoảng [left, right]
        while left < right:
            # Lấy phần tử ở giữa khoảng
            mid = left + (right - left) // 2
            # Nếu nums[mid] nhỏ hơn target, loại bỏ khoảng không thể chứa target là [left, mid], tiếp tục tìm kiếm trong khoảng [mid + 1, right]
            if nums[mid] < target:
                left = mid + 1 
            # Nếu nums[mid] lớn hơn hoặc bằng target, target có thể nằm trong khoảng [left, mid], tiếp tục tìm kiếm trong khoảng [left, mid]
            else:
                right = mid
        # Kiểm tra xem phần tử còn lại trong khoảng có phải là target hay không, nếu không trả về -1
        return left if nums[left] == target else -1

Hung Nguyen 🧠🌳

Explorer