DP Basic

1. Giới thiệu về Quy hoạch động

1.1 Định nghĩa của Quy hoạch động

Quy hoạch động (Dynamic Programming): viết tắt là DP, là một phương pháp giải quyết các vấn đề tối ưu hóa trong quá trình ra quyết định nhiều giai đoạn. Trong quy hoạch động, chúng ta chia bài toán gốc thành các bài toán con tương đối đơn giản hơn, giải quyết trước các bài toán con, sau đó sử dụng kết quả của các bài toán con để tìm kết quả của bài toán gốc.

Quy hoạch động ban đầu được Richard Bellman giới thiệu vào năm 1957 trong cuốn sách “Quy hoạch động (Dynamic Programming)“. Tại đây, từ “Programming” không có nghĩa là lập trình, mà chỉ một phương pháp “xử lý bảng”, tức là lưu trữ kết quả tính toán của mỗi bước vào bảng để sử dụng cho các tính toán sau.

1.2 Ý tưởng cốt lõi của Quy hoạch động

Ý tưởng cốt lõi của Quy hoạch động:

1. Chia bài toán gốc thành “các bài toán con chồng chéo nhau”, mỗi bài toán con được tính toán trong một “giai đoạn”. Sau khi hoàn thành tính toán của một giai đoạn, phương pháp quy hoạch động mới thực hiện tính toán giai đoạn tiếp theo.
2. Trong quá trình giải quyết bài toán con, có 2 phương pháp để tiếp cận là “tính toán từ trên xuống (top-down)” hoặc “tính toán từ dưới lên (bottom-up)” để tìm ra “kết quả của bài toán con”, lưu trữ kết quả này vào bảng. Khi cần tính toán lại bài toán con này, chỉ cần truy vấn kết quả của bài toán con từ bảng, từ đó tránh được việc tính toán lặp lại nhiều lần.

Điều này giống với phương pháp chia để trị, nhưng điểm khác biệt giữa Quy hoạch động và phương pháp chia để trị là:

1. Các vấn đề được giải quyết bằng Quy hoạch động thường có các bài toán con tương quan với nhau, có thể có nhiều bài toán con chồng chéo.
2. Sử dụng phương pháp Quy hoạch động sẽ lưu trữ kết quả của các bài toán con chồng chéo vào bảng, để sử dụng cho các tính toán sau này, từ đó tránh được việc tính toán lặp lại nhiều lần.

1.3 Ví dụ đơn giản về Quy hoạch động

Bây giờ chúng ta hãy sử dụng một ví dụ đơn giản để giới thiệu về Quy hoạch động và sau đó sẽ giải thích các thuật ngữ trong Quy hoạch động.

Dãy Fibonacci: Dãy số Fibonacci bắt đầu từ $f(0)=1,f(1)=2$, các số tiếp theo là tổng của hai số trước đó. Tức là:

$f(n)=\{\begin{array}{ll}0& n=0\\ 1& n=1\\ f(n-2)+f(n-1)& n>1\end{array}$

Dựa trên công thức $f(n)=f(n-2)+f(n-1)$, chúng ta có thể đệ quy chia bài toán gốc $f(n)$ thành hai bài toán con $f(n-2)$ và $f(n-1)$. Quá trình đệ quy tương ứng được mô tả trong hình dưới đây:

Từ hình trên, ta có thể thấy: nếu tính toán $f(5)$ bằng cách sử dụng thuật toán đệ quy truyền thống, ta cần tính toán $f(3)$ và $f(4)$ trước, và khi tính toán $f(4)$ ta cần tính toán $f(3)$ nữa, điều này dẫn đến việc tính toán lặp lại của $f(3)$. Tương tự, $f(0)$, $f(1)$, $f(2)$ đều được tính toán nhiều lần, dẫn đến việc tính toán lặp lại.

Để tránh tính toán lặp lại, chúng ta có thể sử dụng “phương pháp bảng xử lý” trong Quy hoạch động để giải quyết.

Ở đây, chúng ta sử dụng phương pháp “tính toán từ dưới lên” để tìm ra kết quả của các bài toán con $f(n-2)$ và $f(n-1)$, sau đó lưu trữ kết quả này vào bảng, để sử dụng cho các tính toán sau này. Quá trình cụ thể như sau:

1. Định nghĩa một mảng $dp$, được sử dụng để lưu trữ các giá trị trong dãy Fibonacci.
2. Khởi tạo $dp[0]=0,dp[1]=1$.
3. Dựa trên công thức đệ quy của dãy Fibonacci $f(n)=f(n-1)+f(n-2)$, bắt đầu tính toán từ $dp(2)$ để tính toán các số Fibonacci, cho đến khi tính toán được $dp(n)$.
4. Cuối cùng, trả về $dp(n)$ để nhận được số Fibonacci thứ $n$.

Code cụ thể như sau:

class Solution:
    def fib(self, n: int) -> int:
        if n == 0:
            return 0
        if n == 1:
            return 1
 
        dp = [0 for _ in range(n + 1)]
        dp[0] = 0
        dp[1] = 1
 
        for i in range(2, n + 1):
            dp[i] = dp[i - 2] + dp[i - 1]
 
        return dp[n]

Phương pháp này sử dụng bộ nhớ đệm (bảng băm, tập hợp hoặc mảng) để lưu trữ kết quả tính toán, từ đó tránh được tính toán lặp lại của các bài toán con, đây chính là “phương pháp Quy hoạch động”.

2. Đặc điểm của quy hoạch động

Vậy vấn đề nào có thể được giải quyết bằng thuật toán quy hoạch động?

Đầu tiên, vấn đề có thể được giải quyết bằng phương pháp quy hoạch động phải đáp ứng ba đặc điểm sau:

1. Tính chất con tối ưu
2. Tính chất con trùng lặp
3. Tính chất không có tác động sau này

2.1 Tính chất con tối ưu

Tính chất con tối ưu: Đề cập đến việc giải pháp tối ưu của một vấn đề chứa trong nó giải pháp tối ưu của các vấn đề con.

Ví dụ, như hình dưới đây, vấn đề gốc $S=\{a_1,a_2,a_3,a_4\}$, sau bước $a_1$ chúng ta chọn một giải pháp tối ưu hiện tại, vấn đề trở thành việc giải quyết vấn đề con $S_{\text{vaˆˊn đeˆˋ con}}=\{a_2,a_3,a_4\}$. Nếu giải pháp tối ưu của vấn đề gốc có thể được tạo thành từ “giải pháp tối ưu của bước $a_1$” và “giải pháp tối ưu của $S_{\text{vaˆˊn đeˆˋ con}}$”, thì vấn đề đó đáp ứng tính chất con tối ưu.

Nghĩa là, nếu giải pháp tối ưu của vấn đề gốc chứa giải pháp tối ưu của vấn đề con, thì vấn đề đó đáp ứng tính chất con tối ưu.

2.2 Tính chất con trùng lặp

Tính chất con trùng lặp: Đề cập đến việc trong quá trình giải quyết vấn đề con, có rất nhiều vấn đề con bị lặp lại, một vấn đề con có thể được sử dụng nhiều lần trong quá trình ra quyết định của giai đoạn tiếp theo. Nếu có nhiều vấn đề con trùng lặp, chỉ cần giải quyết một lần và lưu kết quả vào bảng, sau đó có thể truy vấn trực tiếp khi cần, không cần giải quyết lại.

Trong ví dụ “dãy Fibonacci” đã đề cập trước đó, $f(0)$, $f(1)$, $f(2)$, $f(3)$ đã được tính toán lại nhiều lần. Thuật toán quy hoạch động sử dụng tính chất con trùng lặp, lưu trữ kết quả của chúng vào bảng trong lần tính toán đầu tiên, và khi sử dụng lại, chỉ cần truy vấn trực tiếp, không cần tính toán lại, từ đó tăng hiệu suất.

2.3 Tính chất không có tác động sau này

Tính chất không có tác động sau này: Đề cập đến việc giải pháp của vấn đề con (giá trị trạng thái) chỉ phụ thuộc vào giai đoạn trước đó và không bị ảnh hưởng bởi quyết định của giai đoạn sau này.

Nghĩa là, một khi giải pháp của một vấn đề con được xác định, nó sẽ không bị thay đổi nữa.

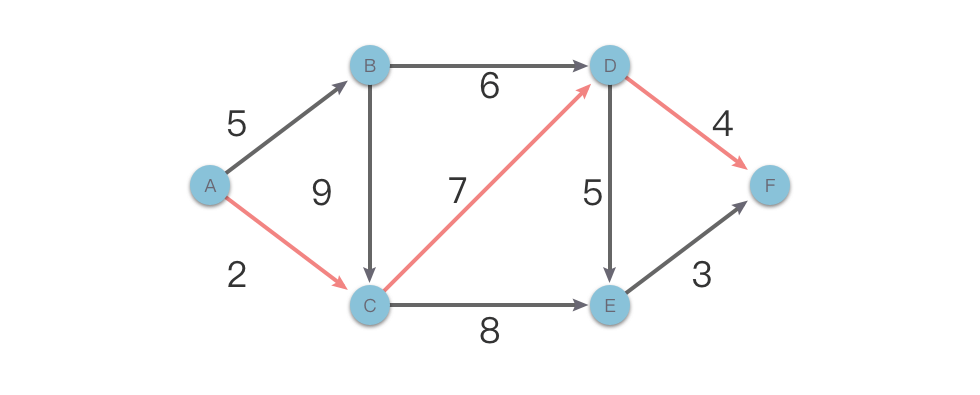
Ví dụ, trong hình dưới đây là một đồ thị có hướng không chu trình với trọng số, khi giải quyết vấn đề tìm đường đi ngắn nhất từ điểm $A$ đến điểm $F$, giả sử chúng ta đã biết đường đi ngắn nhất từ điểm $A$ đến điểm $D$ (độ dài là $2+7=11$). Sau đó, bất kể lựa chọn đường đi sau này như thế nào, độ dài đường đi ngắn nhất từ điểm $A$ đến điểm $D$ không bị ảnh hưởng. Đây chính là tính chất “không có tác động sau này”.

Nếu một vấn đề có “tác động sau này”, có thể cần chuyển đổi hoặc giải quyết theo hướng ngược lại để loại bỏ tác động sau này, sau đó mới có thể sử dụng thuật toán quy hoạch động.

4. Ứng dụng của quy hoạch động

Các vấn đề liên quan đến quy hoạch động thường linh hoạt và phức tạp, không có một cách tiếp cận cụ thể và thường xuyên xuất hiện trong các cuộc thi lập trình và phỏng vấn.

Điểm quan trọng của các vấn đề quy hoạch động là “làm thế nào để thiết kế trạng thái” và “rút ra điều kiện chuyển trạng thái”, cùng với các “phương pháp tối ưu” khác nhau. Cần luyện tập và tổng kết nhiều vấn đề loại này, chỉ khi tiếp xúc với nhiều loại câu hỏi, chúng ta mới có thể thành thạo ý tưởng của quy hoạch động.

Dưới đây là một số bài tập cơ bản về quy hoạch động.

4.1 Số Fibonacci

4.1.1 Đường dẫn đến câu hỏi

• 509. Fibonacci Number

4.1.2 Tóm tắt đề bài

Mô tả: Cho một số nguyên $n$.

Yêu cầu: Tính số Fibonacci thứ $n$.

Giải thích:

• Dãy Fibonacci được định nghĩa như sau:
  • $f(0)=0,f(1)=1$.
  • $f(n)=f(n-1)+f(n-2)$, với $n>1$.
• $0\le n\le 30$.

Ví dụ:

• Ví dụ 1:

Input: n = 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1

• Ví dụ 2:

Input: n = 3
Output: 2
Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2

4.1.3 Ý tưởng giải quyết

1. Phân chia giai đoạn

Chúng ta có thể phân chia giai đoạn theo thứ tự số nguyên từ $0$ đến $n$.

2. Định nghĩa trạng thái

Định nghĩa trạng thái $dp[i]$ là: số Fibonacci thứ $i$.

3. Công thức chuyển trạng thái

Dựa trên định nghĩa dãy Fibonacci trong câu hỏi $f(n)=f(n-1)+f(n-2)$, ta có công thức chuyển trạng thái $dp[i]=dp[i-1]+dp[i-2]$.

4. Điều kiện ban đầu

Dựa trên điều kiện ban đầu trong câu hỏi $f(0)=0,f(1)=1$, ta có điều kiện ban đầu của quy hoạch động là $dp[0]=0,dp[1]=1$.

5. Kết quả cuối cùng

Dựa trên định nghĩa trạng thái, kết quả cuối cùng là $dp[n]$, tức là số Fibonacci thứ $n$ là $dp[n]$.

4.1.4 Code

class Solution:
    def fib(self, n: int) -> int:
        if n <= 1:
            return n
 
        dp = [0] * (n + 1)
        dp[0] = 0
        dp[1] = 1
        for i in range(2, n + 1):
            dp[i] = dp[i - 2] + dp[i - 1]
 
        return dp[n]

4.1.5 Phân tích độ phức tạp

• Độ phức tạp thời gian: $O(n)$. Vòng lặp đơn duy nhất có độ phức tạp thời gian là $O(n)$.
• Độ phức tạp không gian: $O(n)$. Sử dụng một mảng một chiều để lưu trạng thái, vì vậy độ phức tạp không gian tổng thể là $O(n)$.

4.2 Leo cầu thang

4.2.1 Liên kết đến câu hỏi

• 70. Climbing Stairs

4.2.2 Tóm tắt đề bài

Mô tả: Giả sử bạn đang leo cầu thang. Bạn cần $n$ bước để leo lên đầu cầu thang. Mỗi lần bạn có thể leo $1$ hoặc $2$ bước. Cho một số nguyên $n$.

Yêu cầu: Tính số cách khác nhau để leo lên đầu cầu thang.

Giải thích:

• $1\le n\le 45$.

Ví dụ:

• Ví dụ 1:

Input: n = 2
Output: 2
Explanation: Có hai cách để leo lên đầu cầu thang.
1. 1 bước + 1 bước
2. 2 bước

• Ví dụ 2:

Input: n = 3
Output: 3
Explanation: Có ba cách để leo lên đầu cầu thang.
1. 1 bước + 1 bước + 1 bước
2. 1 bước + 2 bước
3. 2 bước + 1 bước

4.2.3 Ý tưởng giải quyết

1. Phân chia giai đoạn

Chúng ta có thể phân chia giai đoạn theo số bước của cầu thang, từ $0$ đến $n$.

2. Định nghĩa trạng thái

Định nghĩa trạng thái $dp[i]$ là: số cách để leo lên bước thứ $i$ của cầu thang.

3. Công thức chuyển trạng thái

Dựa trên yêu cầu đề bài, mỗi lần chỉ có thể leo $1$ hoặc $2$ bước. Vì vậy, bước thứ $i$ của cầu thang chỉ có thể leo lên từ bước $i-1$ hoặc $i-2$. Do đó, ta có công thức chuyển trạng thái $dp[i]=dp[i-1]+dp[i-2]$.

4. Điều kiện ban đầu

• Số cách để leo lên bước $0$ của cầu thang: có thể coi là $1$ cách (leo từ bước $0$ lên bước $0$), tức là $dp[0]=1$.
• Số cách để leo lên bước $1$ của cầu thang: $1$ cách (leo từ bước $0$ lên bước $1$), tức là $dp[1]=1$.
• Số cách để leo lên bước $2$ của cầu thang: $2$ cách (leo từ bước $0$ lên bước $2$, hoặc leo từ bước $1$ lên bước $2$).

5. Kết quả cuối cùng

Dựa trên định nghĩa trạng thái, kết quả cuối cùng là $dp[n]$, tức là số cách để leo lên bước thứ $n$ của cầu thang.

Mặc dù công thức chuyển trạng thái của hai bài toán này đều là $dp[i]=dp[i-1]+dp[i-2]$, nhưng cách tiếp cận của hai bài toán này không giống nhau, điều này cho thấy tính linh hoạt và đa dạng của các bài toán liên quan đến quy hoạch động.

4.2.4 Code

class Solution:
    def climbStairs(self, n: int) -> int:
        dp = [0 for _ in range(n + 1)]
        dp[0] = 1
        dp[1] = 1
        for i in range(2, n + 1):
            dp[i] = dp[i - 1] + dp[i - 2]
        
        return dp[n]

4.2.5 Phân tích độ phức tạp

• Độ phức tạp thời gian: $O(n)$. Vòng lặp đơn duy nhất có độ phức tạp thời gian là $O(n)$.
• Độ phức tạp không gian: $O(n)$. Sử dụng một mảng một chiều để lưu trạng thái, vì vậy độ phức tạp không gian tổng thể là $O(n)$. Vì trạng thái $dp[i]$ chỉ phụ thuộc vào $dp[i-1]$ và $dp[i-2]$, nên có thể sử dụng $3$ biến để lưu trạng thái tương ứng với $dp[i]$, $dp[i-1]$, $dp[i-2]$, từ đó tối ưu không gian đến $O(1)$.

4.3 Đường đi duy nhất

4.3.1 Liên kết đến câu hỏi

• 62. Unique Paths

4.3.2 Tóm tắt đề bài

Mô tả: Cho hai số nguyên $m$ và $n$, đại diện cho một bảng cỡ $m\times n$, một con robot đang ở vị trí góc trên bên trái của bảng. Mỗi lần robot chỉ có thể di chuyển sang phải hoặc xuống dưới một bước.

Yêu cầu: Tính số lượng đường đi khác nhau để robot đi từ góc trên bên trái đến góc dưới bên phải của bảng.

Giải thích:

• $1\le m,n\le 100$.
• Đáp án được bảo đảm nhỏ hơn hoặc bằng $2\times 10^9$.

Ví dụ:

• Ví dụ 1:

Input: m = 3, n = 7
Output: 28

• Ví dụ 2:

Input: m = 3, n = 2
Output: 3
Explanation:
Có 3 đường đi để robot đi từ góc trên bên trái đến góc dưới bên phải.
1. Sang phải -> Xuống dưới -> Xuống dưới
2. Xuống dưới -> Xuống dưới -> Sang phải
3. Xuống dưới -> Sang phải -> Xuống dưới

4.3.3 Ý tưởng giải quyết

1. Phân chia giai đoạn

Chúng ta có thể phân chia giai đoạn dựa trên vị trí kết thúc của đường đi (tạo thành một cặp tọa độ hai chiều gồm hàng và cột).

2. Định nghĩa trạng thái

Định nghĩa trạng thái $dp[i][j]$ là: số lượng đường đi từ góc trên bên trái đến vị trí $(i,j)$ trên bảng.

3. Công thức chuyển trạng thái

Vì chúng ta chỉ có thể di chuyển sang phải hoặc xuống dưới một bước, nên để đến vị trí $(i,j)$, chúng ta chỉ có thể di chuyển từ vị trí $(i-1,j)$ xuống dưới một bước; hoặc từ vị trí $(i,j-1)$ sang phải một bước. Do đó, chúng ta có công thức chuyển trạng thái: $dp[i][j]=dp[i-1][j]+dp[i][j-1]$ với $i>0,j>0$.

4. Điều kiện ban đầu

• Để đến vị trí $(0,0)$, chỉ có một cách, tức là $dp[0][0]=1$.
• Các phần tử trong hàng đầu tiên chỉ có một đường đi (chỉ có thể di chuyển từ phần tử trước đó sang phải), do đó $dp[0][j]=1$.
• Tương tự, các phần tử trong cột đầu tiên chỉ có một đường đi (chỉ có thể di chuyển từ phần tử trên đó xuống dưới), do đó $dp[i][0]=1$.

5. Kết quả cuối cùng

Dựa trên định nghĩa trạng thái, kết quả cuối cùng là $dp[m-1][n-1]$, tức là số lượng đường đi từ góc trên bên trái đến vị trí $(m-1,n-1)$ trên bảng.

4.3.4 Code

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = [[0 for _ in range(n)] for _ in range(m)]
        
        for j in range(n):
            dp[0][j] = 1
        for i in range(m):
            dp[i][0] = 1
 
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
        
        return dp[m - 1][n - 1]

4.3.5 Phân tích độ phức tạp

• Độ phức tạp thời gian: $O(m\times n)$. Vòng lặp đôi duy nhất có độ phức tạp thời gian là $O(m\times n)$.
• Độ phức tạp không gian: $O(m\times n)$. Sử dụng một mảng hai chiều để lưu trạng thái, vì vậy độ phức tạp không gian tổng thể là $O(m\times n)$. Tuy nhiên, vì trạng thái $dp[i][j]$ chỉ phụ thuộc vào $dp[i-1][j]$ và $dp[i][j-1]$, và chúng ta duyệt qua các phần tử theo thứ tự từ trên xuống dưới, từ trái sang phải, nên có thể sử dụng một mảng một chiều có độ dài $m$ để lưu trạng thái, từ đó tối ưu không gian đến $O(m)$.