Selection Sort

Sắp xếp chọn

1. Ý tưởng thuật toán sắp xếp chọn

Sắp xếp chọn (Selection Sort) cơ bản:
Chia mảng thành hai phần: phần đã sắp xếp và phần chưa sắp xếp. Mỗi lần lặp, chọn phần tử nhỏ nhất từ phần chưa sắp xếp và đặt nó vào cuối phần đã sắp xếp, từ đó chuyển phần tử đó vào phần đã sắp xếp.

Sắp xếp chọn là một thuật toán sắp xếp đơn giản và trực quan, ý tưởng của nó đơn giản và mã code cũng tương đối dễ hiểu.

2. Bước thực hiện thuật toán sắp xếp chọn

Giả sử mảng có $n$ phần tử, các bước thực hiện thuật toán sắp xếp chọn như sau:

Ban đầu, không có phần tử nào đã được sắp xếp, phần tử chưa sắp xếp là $[0, n - 1]$ .
Bước lặp thứ $1$ $1$ :
1. Duyệt qua phần tử chưa sắp xếp $[0, n - 1]$ , sử dụng biến $min\underline{}i$ để ghi nhận vị trí của phần tử nhỏ nhất trong phần tử chưa sắp xếp.
2. Hoán đổi vị trí của $min\underline{}i$ với phần tử ở vị trí $0$ . Nếu phần tử ở vị trí $0$ chính là phần tử nhỏ nhất, không cần hoán đổi.
3. Lúc này, $[0, 0]$ là phần tử đã sắp xếp, $[1, n - 1]$ (tổng cộng $n - 1$ phần tử) là phần tử chưa sắp xếp.
Bước lặp thứ $2$ $2$ :
1. Duyệt qua phần tử chưa sắp xếp $[1, n - 1]$ , sử dụng biến $min\underline{}i$ để ghi nhận vị trí của phần tử nhỏ nhất trong phần tử chưa sắp xếp.
2. Hoán đổi vị trí của $min\underline{}i$ với phần tử ở vị trí $1$ . Nếu phần tử ở vị trí $1$ chính là phần tử nhỏ nhất, không cần hoán đổi.
3. Lúc này, $[0, 1]$ là phần tử đã sắp xếp, $[2, n - 1]$ (tổng cộng $n - 2$ phần tử) là phần tử chưa sắp xếp.
Tiếp tục như vậy, lặp lại quá trình chọn cho phần tử chưa sắp xếp, cho đến khi tất cả các phần tử đều được chuyển vào phần tử đã sắp xếp, quá trình sắp xếp kết thúc.

Chúng ta lấy ví dụ với mảng $[20, 12, 10, 15, 2]$ , để mô phỏng toàn bộ quá trình sắp xếp chọn.

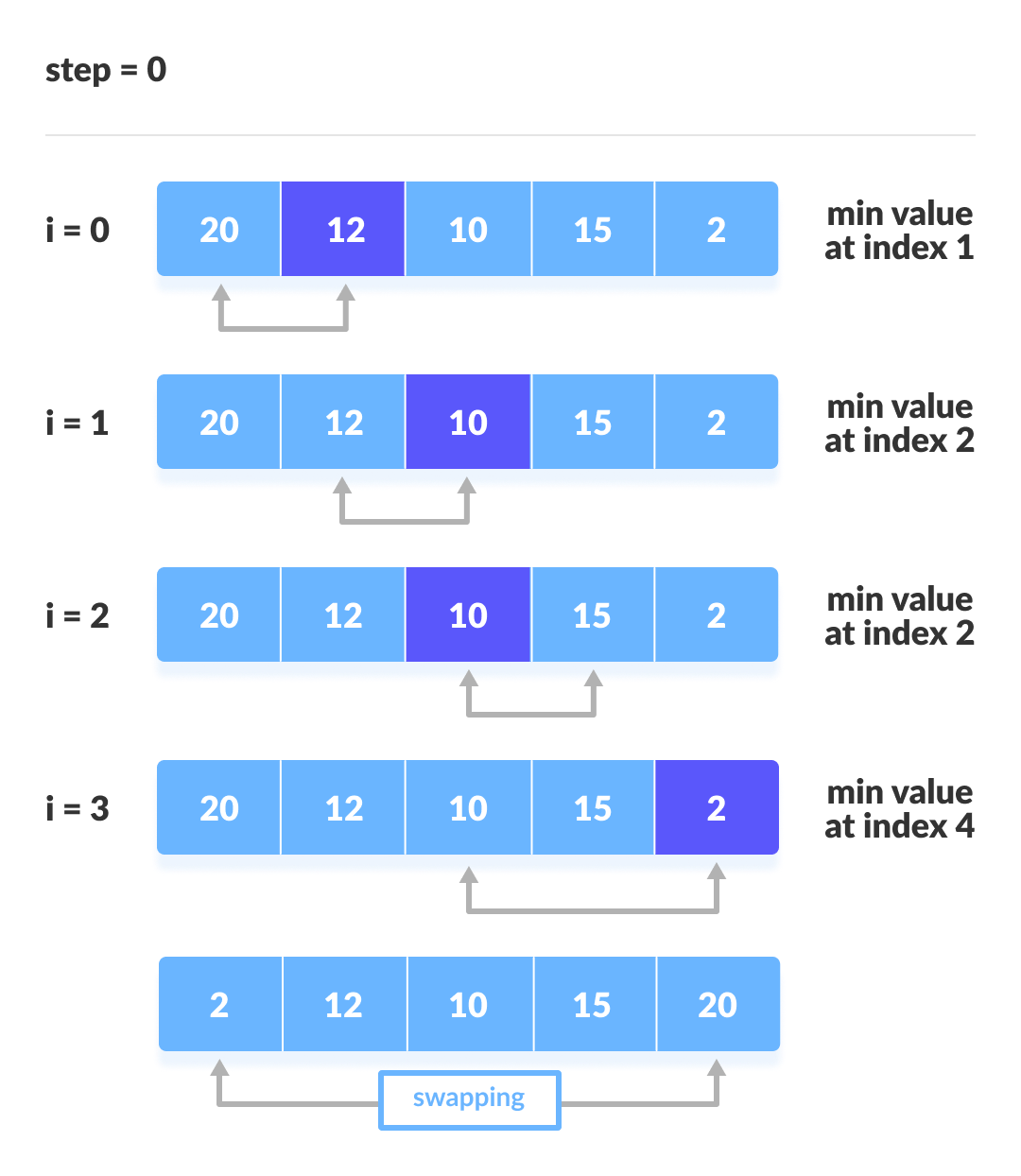
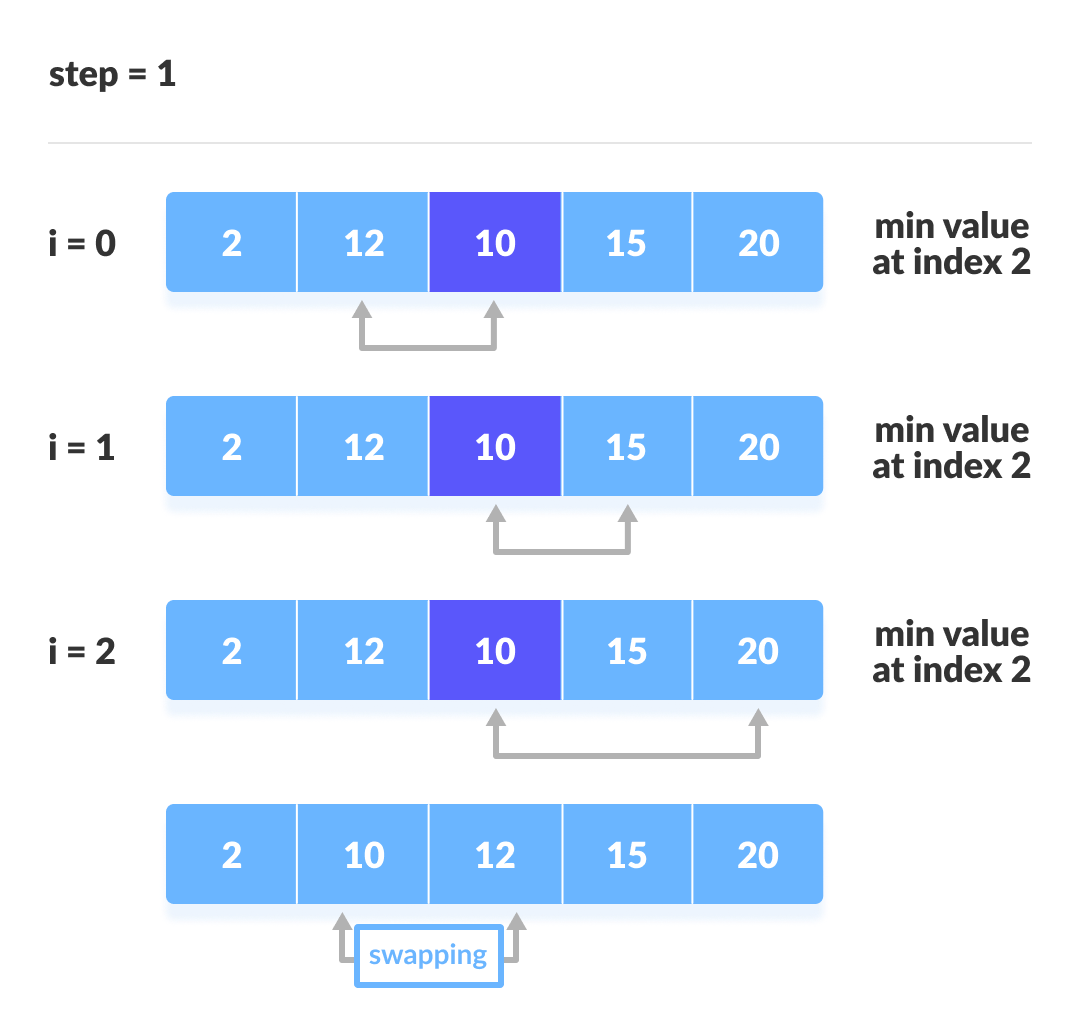
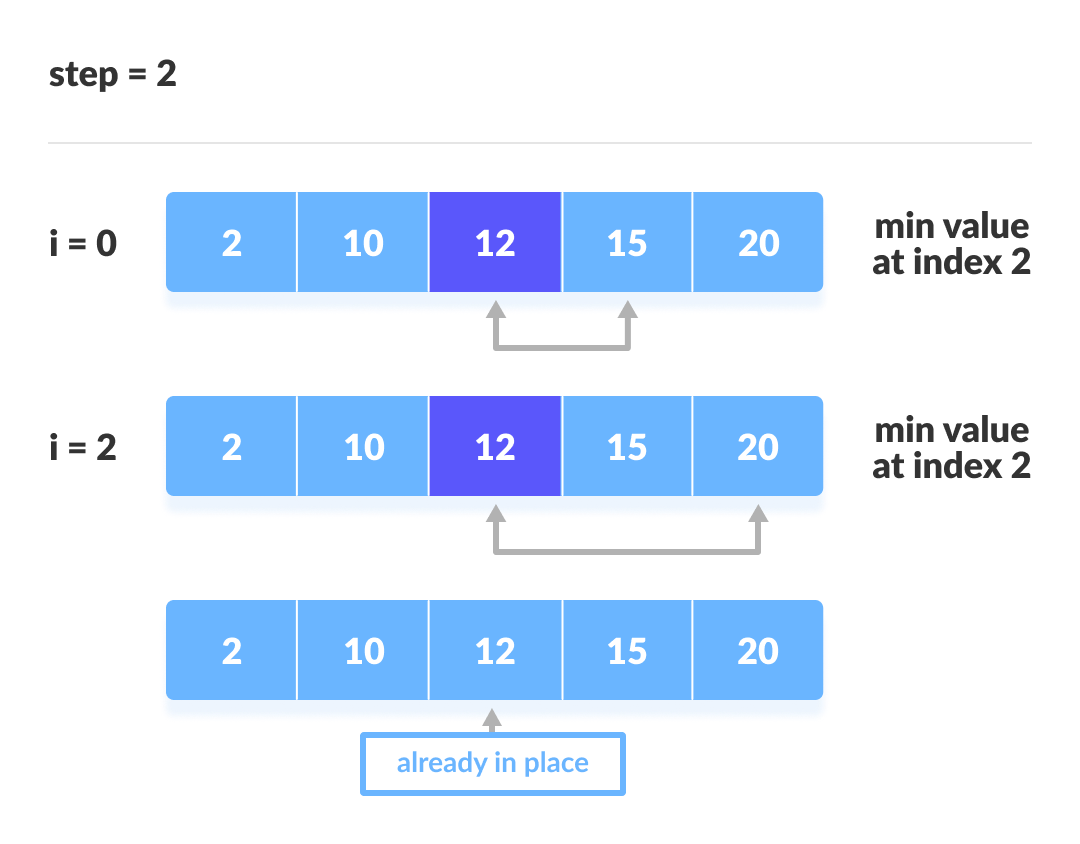
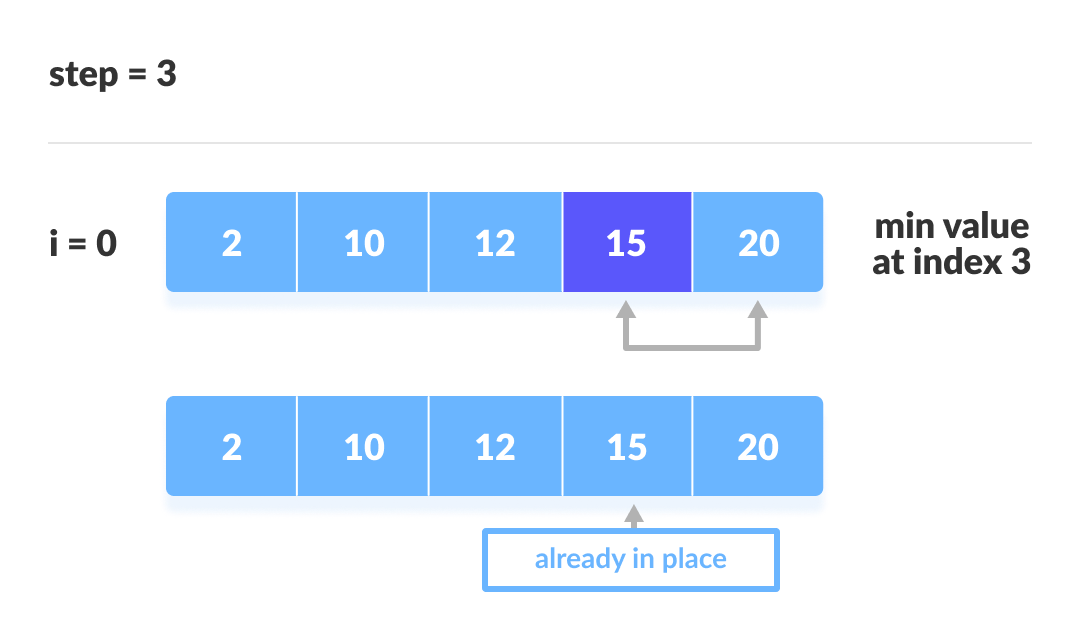
3. Cài đặt mã sắp xếp chọn

class Solution:
    def selectionSort(self, nums: [int]) -> [int]:
        for i in range(len(nums) - 1):
            # Ghi nhận vị trí của phần tử nhỏ nhất trong phần tử chưa sắp xếp
            min_i = i
            for j in range(i + 1, len(nums)):
                if nums[j] < nums[min_i]:
                    min_i = j
            # Nếu tìm thấy vị trí của phần tử nhỏ nhất, hoán đổi vị trí của phần tử ở vị trí i với phần tử nhỏ nhất
            if i != min_i:
                nums[i], nums[min_i] = nums[min_i], nums[i]
        return nums

    def sortArray(self, nums: [int]) -> [int]:
        return self.selectionSort(nums)

4. Phân tích thuật toán sắp xếp chọn

Độ phức tạp thời gian: $O(n^2)$ $O (n^{2})$ . Số lần so sánh giữa các phần tử trong quá trình sắp xếp không phụ thuộc vào trạng thái ban đầu của dãy, độ phức tạp thời gian luôn là $O(n^2)$ $O (n^{2})$ .
- Điều này là do trong mọi trường hợp, số lần so sánh giữa các phần tử trong quá trình sắp xếp đều như nhau, là $∑^n_{i=2}(i - 1) = \frac{n(n−1)}{2}$ lần.
Độ phức tạp không gian: $O(1)$ . Thuật toán sắp xếp chọn là thuật toán sắp xếp trên chính mảng ban đầu, chỉ sử dụng các biến con trỏ $i$ , $j$ và vị trí phần tử nhỏ nhất $min\underline{}i$ tương ứng với các biến hằng số.
Tính ứng dụng của thuật toán sắp xếp chọn: Phương pháp sắp xếp chọn di chuyển phần tử nhiều lần trong quá trình sắp xếp và hiệu suất thời gian của nó khá thấp. Do đó, phương pháp sắp xếp chọn thích hợp cho các trường hợp dữ liệu đầu vào có kích thước nhỏ, đặc biệt là khi trạng thái ban đầu của dãy đã gần như được sắp xếp.
Tính ổn định của thuật toán sắp xếp chọn: Vì hoán đổi vị trí giữa phần tử nhỏ nhất và phần tử chưa sắp xếp chỉ diễn ra giữa các phần tử không kề nhau, có thể thay đổi thứ tự tương đối của các phần tử bằng nhau, do đó, thuật toán sắp xếp chọn là một thuật toán sắp xếp không ổn định.