Quick Sort

Sắp xếp nhanh

1. Ý tưởng thuật toán sắp xếp nhanh

Sắp xếp nhanh (Quick Sort):
Sử dụng chiến lược chia để trị, chọn một phần tử trong mảng làm phần tử chốt, thông qua một lần sắp xếp để chia mảng thành hai mảng con độc lập, một mảng con chứa tất cả các phần tử nhỏ hơn phần tử chốt và một mảng con chứa tất cả các phần tử lớn hơn phần tử chốt. Sau đó, tiếp tục sắp xếp nhanh đệ quy trên hai mảng con để đạt được mảng hoàn chỉnh đã được sắp xếp.

2. Các bước của thuật toán sắp xếp nhanh

Giả sử mảng có n phần tử, các bước của thuật toán Quick Sort như sau:

Phân chia: Chọn một phần tử chốt và di chuyển tất cả các phần tử lớn hơn phần tử chốt vào bên phải của nó và tất cả các phần tử nhỏ hơn phần tử chốt vào bên trái của nó.
1. Chọn một phần tử chốt pivot từ mảng hiện tại (ở đây chúng ta chọn phần tử đầu tiên của mảng làm phần tử chốt, tức là pivot = nums[low]).
2. Sử dụng con trỏ left trỏ đến vị trí bắt đầu của mảng và con trỏ right trỏ đến vị trí cuối của mảng.
3. Di chuyển con trỏ right từ phải sang trái để tìm phần tử đầu tiên nhỏ hơn phần tử chốt.
4. Di chuyển con trỏ left từ trái sang phải để tìm phần tử đầu tiên lớn hơn phần tử chốt.
5. Hoán đổi vị trí của hai phần tử mà con trỏ left và right đang trỏ đến.
6. Lặp lại bước 3 đến 5 cho đến khi con trỏ left và right gặp nhau, sau đó đặt phần tử chốt vào vị trí giữa hai mảng con.
Phân rã đệ quy: Sau khi phân chia xong, tiếp tục sắp xếp nhanh đệ quy trên hai mảng con đã được phân chia.
1. Chia mảng thành hai mảng con bằng cách sử dụng vị trí của phần tử chốt.
2. Đệ quy sắp xếp nhanh trên hai mảng con, một mảng con từ vị trí đầu đến vị trí phần tử chốt trừ 1, một mảng con từ vị trí phần tử chốt cộng 1 đến vị trí cuối.
Kết thúc đệ quy: Khi mỗi mảng con chỉ còn một phần tử, quá trình sắp xếp kết thúc.

Chúng ta sẽ lấy ví dụ với mảng sau để minh họa toàn bộ quá trình sắp xếp nhanh.

Hãy xem quá trình "Phân chia" một lần.

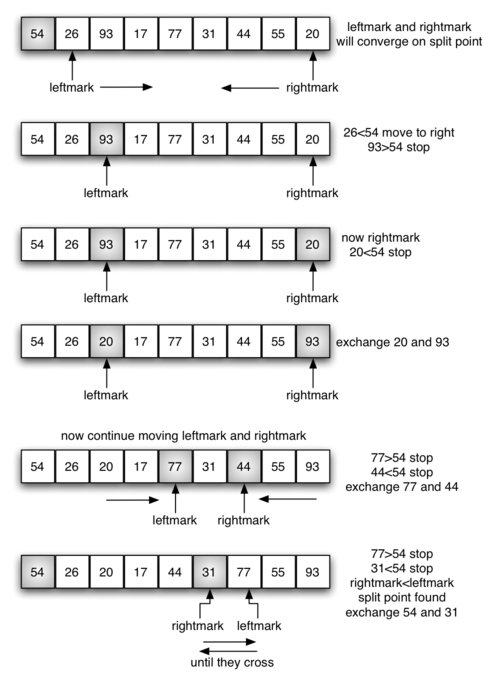
Sau khi hoàn thành một lần "Phân chia", mảng được chia thành mảng con trái, phần tử chốt và mảng con phải. Tiếp theo, chỉ cần đệ quy sắp xếp nhanh trên hai mảng con đã chia để hoàn thành quá trình sắp xếp.

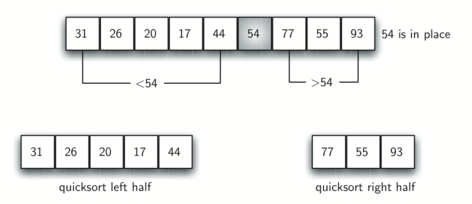
3. Cài đặt mã của sắp xếp nhanh

import random

class Solution:
    # Phân chia ngẫu nhiên: Chọn một phần tử ngẫu nhiên từ nums[low: high + 1] và thực hiện sắp xếp dịch chuyển
    def randomPartition(self, nums: [int], low: int, high: int) -> int:
        # Chọn một phần tử ngẫu nhiên
        i = random.randint(low, high)
        # Hoán đổi phần tử chốt với phần tử ở vị trí thấp nhất
        nums[i], nums[low] = nums[low], nums[i]
        # Sắp xếp dịch chuyển để di chuyển tất cả các phần tử lớn hơn phần tử chốt vào bên phải và tất cả các phần tử nhỏ hơn phần tử chốt vào bên trái. Cuối cùng, đặt phần tử chốt vào vị trí chính xác
        return self.partition(nums, low, high)
    
    # Phân chia: Chọn phần tử đầu tiên nums[low] làm phần tử chốt, sau đó di chuyển tất cả các phần tử nhỏ hơn phần tử chốt vào bên trái và tất cả các phần tử lớn hơn phần tử chốt vào bên phải. Cuối cùng, đặt phần tử chốt vào vị trí chính xác
    def partition(self, nums: [int], low: int, high: int) -> int:
        # Chọn phần tử đầu tiên làm phần tử chốt
        pivot = nums[low]
        
        i, j = low, high
        while i < j:
            # Di chuyển con trỏ j từ phải sang trái để tìm phần tử đầu tiên nhỏ hơn phần tử chốt
            while i < j and nums[j] >= pivot:
                j -= 1
            # Di chuyển con trỏ i từ trái sang phải để tìm phần tử đầu tiên lớn hơn phần tử chốt
            while i < j and nums[i] <= pivot:
                i += 1
            # Hoán đổi vị trí của hai phần tử mà con trỏ i và j đang trỏ đến
            nums[i], nums[j] = nums[j], nums[i]
        
        # Đặt phần tử chốt vào vị trí chính xác
        nums[i], nums[low] = nums[low], nums[i]
        # Trả về chỉ số của phần tử chốt
        return i

    def quickSort(self, nums: [int], low: int, high: int) -> [int]:
        if low < high:
            # Chia mảng thành hai mảng con bằng cách sử dụng vị trí của phần tử chốt
            pivot_i = self.randomPartition(nums, low, high)
            # Đệ quy sắp xếp nhanh trên hai mảng con
            self.quickSort(nums, low, pivot_i - 1)
            self.quickSort(nums, pivot_i + 1, high)

        return nums

    def sortArray(self, nums: [int]) -> [int]:
        return self.quickSort(nums, 0, len(nums) - 1)

4. Phân tích thuật toán sắp xếp nhanh

Độ phức tạp thời gian của thuật toán Quick Sort chủ yếu phụ thuộc vào việc chọn phần tử chốt. Trong bài viết này, chúng ta chọn phần tử đầu tiên của mảng làm phần tử chốt.

Trong trường hợp này, nếu các phần tử tham gia sắp xếp đã được sắp xếp ban đầu, phương pháp Quick Sort sẽ mất thời gian lâu nhất. Điều này dẫn đến độ phức tạp thời gian tệ nhất.

Trong trường hợp này, sau khi hoàn thành lần sắp xếp đầu tiên, số lần so sánh là $(n-1) + (n-2) + … + 1 = \frac{n(n-1)}{2}$ . Do đó, độ phức tạp thời gian trong trường hợp này là $O(n^2)$ , cũng là độ phức tạp thời gian tệ nhất.

Chúng ta có thể cải tiến việc chọn phần tử chốt. Nếu mỗi lần chúng ta chọn phần tử chốt sao cho nó chính xác chia mảng hiện tại thành hai phần bằng nhau, tức là chọn phần tử trung vị của mảng hiện tại.

Trong trường hợp này, mỗi lần chúng ta chọn phần tử chốt, mảng được chia thành hai mảng con có số phần tử giống nhau. Thời gian phức tạp của thuật toán trong trường hợp này được tính bằng công thức $T(n) = 2 \times T(\frac{n}{2}) + \Theta(n)$ . Dựa trên định lý chính, ta có $T(n) = O(n \times \log n)$ , cũng là độ phức tạp thời gian tốt nhất.

Trong trường hợp trung bình, chúng ta có thể chọn một phần tử ngẫu nhiên từ mảng hiện tại làm phần tử chốt. Điều này đảm bảo rằng mỗi lần chọn phần tử chốt được coi là ngẫu nhiên. Thời gian phức tạp trung bình trong trường hợp này là $O(n \times \log n)$ .

Dưới đây là tổng kết:

Độ phức tạp thời gian tốt nhất: $O(n \times \log n)$ . Mỗi lần chọn phần tử chốt đều là phần tử trung vị của mảng hiện tại, thời gian phức tạp của thuật toán thỏa mãn công thức đệ quy $T(n) = 2 \times T(\frac{n}{2}) + \Theta(n)$ , dựa trên định lý chính ta có $T(n) = O(n \times \log n)$ .
Độ phức tạp thời gian tệ nhất: $O(n^2)$ . Mỗi lần chọn phần tử chốt là phần tử cuối cùng của mảng, thời gian phức tạp của thuật toán thỏa mãn công thức đệ quy $T(n) = T(n - 1) + \Theta(n)$ , tổng cộng ta có $T(n) = O(n^2)$ .
Độ phức tạp thời gian trung bình: $O(n \times \log n)$ . Trong trường hợp trung bình, mỗi lần chúng ta chọn phần tử chốt có thể xem là ngẫu nhiên. Thời gian phức tạp trung bình là $O(n \times \log n)$ .
Độ phức tạp không gian: $O(n)$ . Dù cho thuật toán Quick Sort có đệ quy hay không, trong quá trình sắp xếp, chúng ta cần sử dụng không gian phụ như stack hoặc các cấu trúc dữ liệu khác để lưu trữ vị trí đầu và cuối của mảng đang được sắp xếp. Trong trường hợp tệ nhất, độ phức tạp không gian là $O(n)$ . Nếu chúng ta thực hiện một số thay đổi trong thuật toán, sau mỗi lần sắp xếp, so sánh độ dài của hai mảng con được tạo ra và sắp xếp trước mảng con có độ dài ngắn hơn trước tiên, độ phức tạp không gian có thể giảm xuống $O(\log_2 n)$ .
Tính ổn định của sắp xếp: Trong quá trình phân chia, phần tử chốt có thể được hoán đổi sang phía bên phải của các phần tử bằng nhau. Do đó, Quick Sort là một thuật toán không ổn định.