Heap Sort

"Heap sort" là một thuật toán sắp xếp hiệu quả dựa trên cấu trúc "Heap". Trước khi giới thiệu về "Heap sort", chúng ta hãy tìm hiểu về cấu trúc [[Heap]] trước.

1.1 Ý tưởng thuật toán Heap Sort

Ý tưởng cơ bản của thuật toán Heap Sort:
Sử dụng cấu trúc "Heap" để thiết kế thuật toán sắp xếp. Chuyển mảng thành một "Max Heap", lặp lại việc lấy ra nút có giá trị lớn nhất từ Heap và duy trì tính chất của Max Heap cho phần còn lại của Heap.

1.2 Các bước của thuật toán Heap Sort

Xây dựng Max Heap ban đầu:
1. Định nghĩa một cấu trúc Heap được triển khai bằng mảng, lưu trữ các phần tử của mảng gốc vào cấu trúc Heap một cách tuần tự (thứ tự ban đầu không thay đổi).
2. Bắt đầu từ vị trí giữa của mảng, từ phải sang trái, sử dụng "điều chỉnh xuống" để chuyển mảng thành một Max Heap.
Hoán đổi và điều chỉnh Heap:
1. Hoán đổi phần tử đỉnh Heap (phần tử thứ nhất) với phần tử cuối cùng của Heap (phần tử cuối cùng), sau đó giảm kích thước của Heap đi $1$ .
2. Sau khi hoán đổi phần tử, do phần tử đỉnh Heap đã thay đổi, cần bắt đầu từ nút gốc và sử dụng "điều chỉnh xuống" để duy trì tính chất của Heap.
Lặp lại hoán đổi và điều chỉnh Heap:
1. Lặp lại bước $2$ , cho đến khi kích thước của Heap là $1$ , khi đó mảng Heap đã được sắp xếp hoàn toàn.

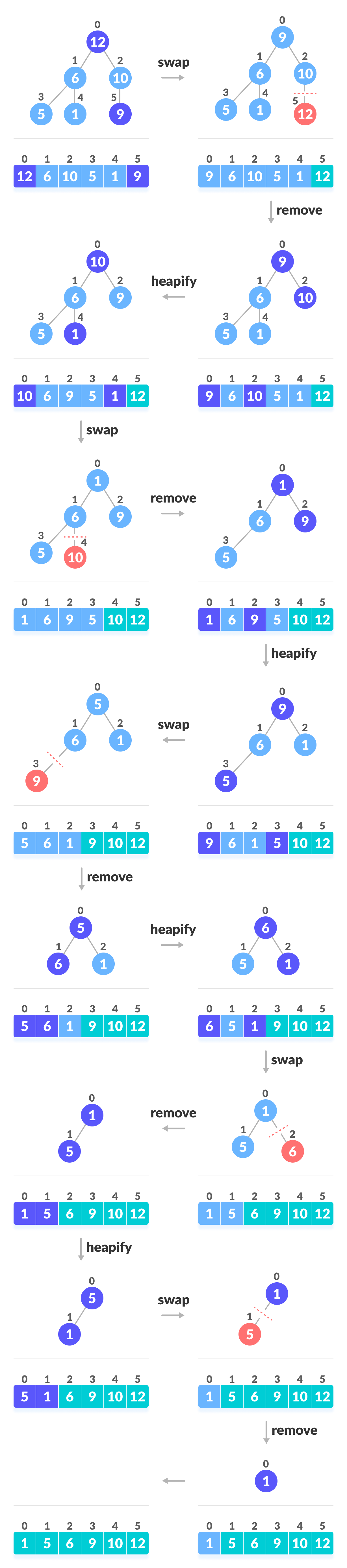
1.3 Triển khai mã Heap Sort

class MaxHeap:
    ......
    def __buildMaxHeap(self, nums: [int]):
        size = len(nums)
        # Đầu tiên, thêm các phần tử của mảng nums vào max_heap theo thứ tự
        for i in range(size):
            self.max_heap.append(nums[i])
        
        # Bắt đầu từ nút không phải lá cuối cùng, thực hiện điều chỉnh xuống
        for i in range((size - 2) // 2, -1, -1):
            self.__shift_down(i, size)

    def maxHeapSort(self, nums: [int]) -> [int]:
        # Xây dựng Max Heap ban đầu dựa trên mảng nums
        self.__buildMaxHeap(nums)
        
        size = len(self.max_heap)
        for i in range(size - 1, -1, -1):
            # Hoán đổi nút gốc với nút cuối cùng của Heap
            self.max_heap[0], self.max_heap[i] = self.max_heap[i], self.max_heap[0]
            # Bắt đầu từ nút gốc, thực hiện điều chỉnh xuống cho Heap hiện tại
            self.__shift_down(0, i)
        
        # Trả về mảng đã được sắp xếp
        return self.max_heap
    
class Solution:
    def maxHeapSort(self, nums: [int]) -> [int]:
        return MaxHeap().maxHeapSort(nums)
        
    def sortArray(self, nums: [int]) -> [int]:
        return self.maxHeapSort(nums)
    
print(Solution().sortArray([10, 25, 6, 8, 7, 1, 20, 23, 16, 19, 17, 3, 18, 14]))

1.4 Phân tích thuật toán Heap Sort

Độ phức tạp thời gian: $O(n \times \log n)$ $O (n \times lo g n)$ .
- Thời gian của thuật toán Heap Sort chủ yếu được tiêu tốn ở hai khía cạnh: "xây dựng Max Heap ban đầu" và "điều chỉnh xuống".
- Giả sử cây nhị phân tương ứng với mảng gốc có độ sâu $d$ $d$ , thuật toán gồm hai vòng lặp độc lập:
  1. Trong vòng lặp đầu tiên, khi xây dựng Heap ban đầu, bắt đầu từ tầng $i = d - 1$ và kết thúc ở tầng $i = 1$ , thuật toán thực hiện một lần điều chỉnh Heap cho mỗi nút nhánh. Một lần điều chỉnh Heap cho một nhánh từ tầng $i$ đến tầng $d$ tương ứng với một khoảng cách tối đa mà nút gốc của nhánh đó có thể di chuyển, tức là $d - i$ . Nhánh trên tầng $i$ có tối đa $2^{i-1}$ nút, do đó thời gian cần để thực hiện một lần điều chỉnh Heap là tổng của số nút trên tầng đó và khoảng cách tối đa mà chúng có thể di chuyển, tức là $\sum_{i = d - 1}^1 2^{i-1} (d-i) = \sum_{j = 1}^{d-1} 2^{d-j-1} \times j = \sum_{j = 1}^{d-1} 2^{d-1} \times {j \over 2^j} \le n \times \sum_{j = 1}^{d-1} {j \over 2^j} < 2 \times n$ . Do đó, thời gian của phần này là $O(n)$ .
  2. Trong vòng lặp thứ hai, mỗi lần điều chỉnh Heap, nút có thể di chuyển tối đa là độ sâu của cây nhị phân, tức là $d = \lfloor \log_2(n) \rfloor + 1$ . Tổng cộng có $n - 1$ lần điều chỉnh Heap, do đó thời gian của vòng lặp thứ hai là $(n-1)(\lfloor \log_2 (n)\rfloor + 1) = O(n \times \log n)$ .
- Vì vậy, độ phức tạp thời gian của thuật toán Heap Sort là $O(n \times \log n)$ .
Độ phức tạp không gian: $O(1)$ . Vì trong thuật toán Heap Sort chỉ cần sử dụng một không gian phụ để lưu trữ kích thước của Heap, nên độ phức tạp không gian là $O(1)$ .
Tính ổn định của thuật toán: Khi thực hiện "điều chỉnh xuống", vị trí tương đối của các phần tử bằng nhau có thể thay đổi. Do đó, Heap Sort là một thuật toán không ổn định.