Merge Sort

Sắp xếp trộn

1. Ý tưởng thuật toán sắp xếp trộn

Sắp xếp trộn (Merge Sort) là một thuật toán sắp xếp sử dụng phương pháp chia để trị, trước tiên chia mảng hiện tại thành hai phần bằng nhau, sau đó kết hợp hai mảng đã sắp xếp thành một mảng đã sắp xếp.

2. Các bước của thuật toán sắp xếp trộn

Giả sử mảng có n phần tử, các bước của thuật toán sắp xếp trộn như sau:

Quá trình chia : Đầu tiên, chia mảng hiện tại thành hai phần bằng nhau đệ quy cho đến khi độ dài của mảng con là $1$ $1$ .
1. Tìm vị trí giữa $mid$ của mảng và chia mảng thành hai mảng con trái $left\underline{}nums$ và phải $right\underline{}nums$ .
2. Đệ quy chia mảng con trái $left\underline{}nums$ và mảng con phải $right\underline{}nums$ .
3. Cuối cùng, mảng được chia thành $n$ mảng con có độ dài bằng $1$ và đã được sắp xếp.
Quá trình trộn : Bắt đầu từ các mảng con đã sắp xếp có độ dài $1$ $1$ , lần lượt trộn hai mảng con để tạo ra một mảng con đã sắp xếp có độ dài $2$ $2$ , sau đó tiếp tục trộn cho đến khi có một mảng con đã sắp xếp có độ dài $n$ $n$ .
1. Sử dụng một mảng kết quả để lưu trữ mảng $nums$ đã trộn.
2. Sử dụng hai con trỏ $left\underline{}i$ và $right\underline{}i$ để chỉ đến vị trí bắt đầu của hai mảng con trái $left\underline{}nums$ và phải $right\underline{}nums$ .
3. So sánh các phần tử tại vị trí $left\underline{}i$ và $right\underline{}i$ và lưu trữ phần tử nhỏ hơn vào mảng kết quả $nums$ .
4. Lặp lại bước $3$ cho đến khi một trong hai con trỏ đến cuối mảng con tương ứng.
5. Sao chép các phần tử còn lại của mảng con chưa đến cuối vào mảng kết quả $nums$ .
6. Trả về mảng $nums$ đã được sắp xếp trộn.

Chúng ta sẽ lấy ví dụ với mảng $[6, 5, 12, 10, 9, 1]$ để minh họa toàn bộ quá trình sắp xếp trộn.

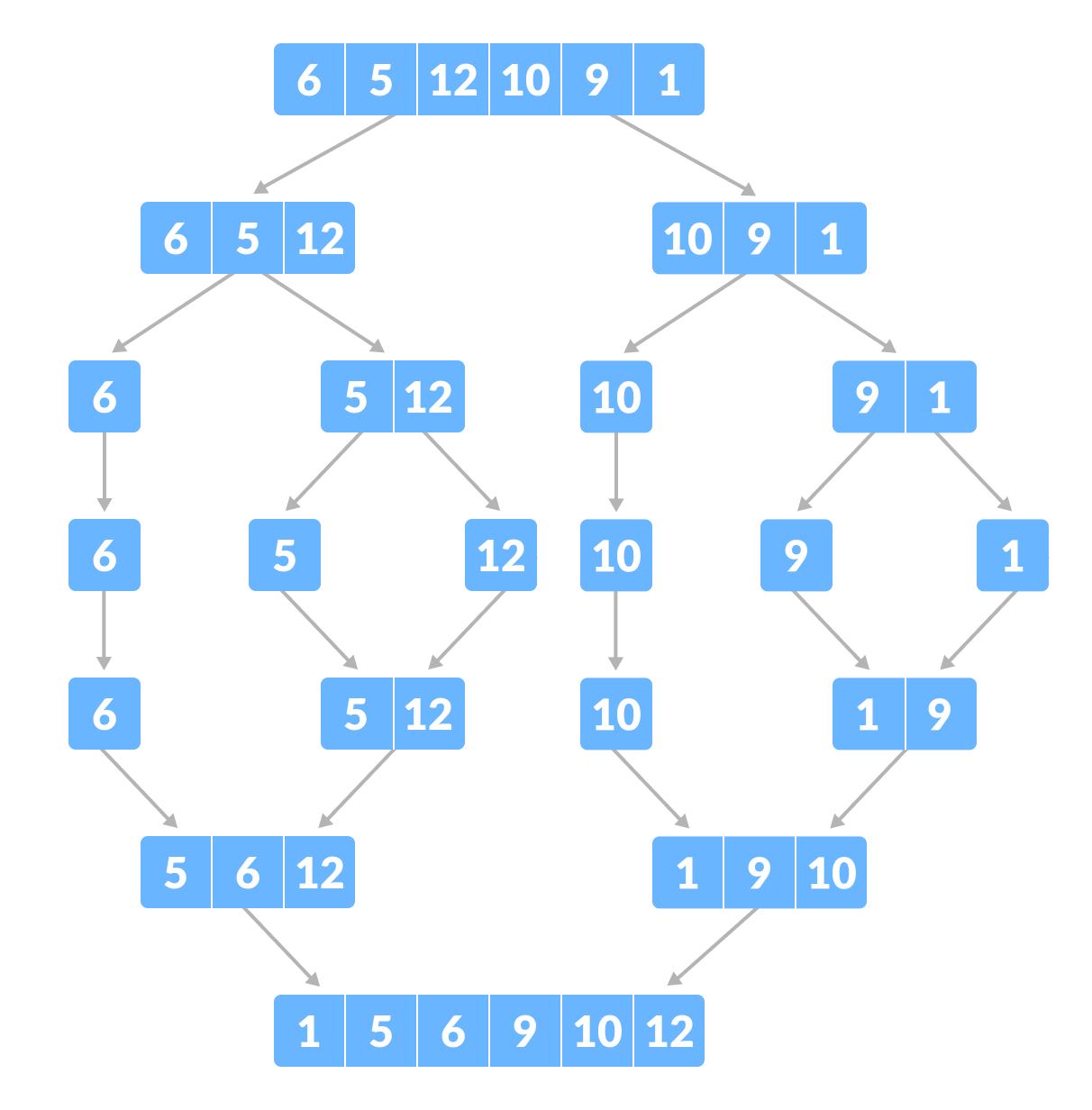
3. Cài đặt mã của sắp xếp trộn

class Solution:
    # Quá trình trộn
    def merge(self, left_nums: [int], right_nums: [int]):
        nums = []
        left_i, right_i = 0, 0
        while left_i < len(left_nums) and right_i < len(right_nums):
            # Lưu trữ phần tử nhỏ hơn vào mảng kết quả
            if left_nums[left_i] < right_nums[right_i]:
                nums.append(left_nums[left_i])
                left_i += 1
            else:
                nums.append(right_nums[right_i])
                right_i += 1
        
        # Sao chép các phần tử còn lại của mảng con chưa đến cuối vào mảng kết quả
        while left_i < len(left_nums):
            nums.append(left_nums[left_i])
            left_i += 1
        
        # Sao chép các phần tử còn lại của mảng con chưa đến cuối vào mảng kết quả
        while right_i < len(right_nums):
            nums.append(right_nums[right_i])
            right_i += 1
        
        # Trả về mảng đã trộn đã sắp xếp
        return nums

    # Quá trình chia
    def mergeSort(self, nums: [int]) -> [int]:
        # Trường hợp số phần tử của mảng nhỏ hơn hoặc bằng 1, trả về mảng ban đầu
        if len(nums) <= 1:
            return nums
        
        mid = len(nums) // 2                        # Tìm vị trí giữa của mảng
        left_nums = self.mergeSort(nums[0: mid])    # Đệ quy sắp xếp mảng con trái
        right_nums =  self.mergeSort(nums[mid:])    # Đệ quy sắp xếp mảng con phải
        return self.merge(left_nums, right_nums)    # Trộn hai mảng con đã sắp xếp

    def sortArray(self, nums: [int]) -> [int]:
        return self.mergeSort(nums)

4. Phân tích thuật toán sắp xếp trộn

Độ phức tạp thời gian: . Độ phức tạp thời gian của thuật toán sắp xếp trộn là tích của số lần trộn và độ phức tạp thời gian của mỗi lần trộn. Quá trình trộn merge(left_nums, right_nums): có độ phức tạp thời gian là , do đó, độ phức tạp thời gian của thuật toán sắp xếp trộn là .
Độ phức tạp không gian: . Thuật toán sắp xếp trộn cần sử dụng một không gian phụ có kích thước bằng với kích thước của mảng đầu vào. Do đó, độ phức tạp không gian của thuật toán là .
Tính ổn định của sắp xếp: Trong quá trình trộn hai mảng con đã sắp xếp, nếu có các phần tử bằng nhau, thuật toán merge(left_nums, right_nums): sẽ đảm bảo phần tử từ mảng con trái được sao chép trước, đảm bảo tính ổn định của thuật toán sắp xếp trộn. Do đó, thuật toán sắp xếp trộn là một thuật toán ổn định.