Insertion Sort

Sắp xếp chèn

1. Ý tưởng của thuật toán sắp xếp chèn

Thuật toán sắp xếp chèn (Insertion Sort):
Chia mảng thành hai phần: phần bên trái là phần đã được sắp xếp, phần bên phải là phần chưa được sắp xếp. Mỗi lần lấy một phần tử từ phần chưa được sắp xếp và chèn vào vị trí thích hợp trong phần đã được sắp xếp.

Trong thuật toán sắp xếp chèn, mỗi lần chèn một phần tử, phần tử đó sẽ được chèn vào vị trí thích hợp trong phần đã được sắp xếp. Do đó, sau mỗi lần chèn, phần đã được sắp xếp vẫn giữ được tính chất đã sắp xếp.

2. Các bước của thuật toán sắp xếp chèn

Giả sử mảng có n phần tử, các bước của thuật toán sắp xếp chèn như sau:

Ban đầu, phần đã được sắp xếp là phần tử đầu tiên của mảng, tức là phần tử ở vị trí 0. Phần chưa được sắp xếp là các phần tử từ vị trí 1 đến vị trí n-1.
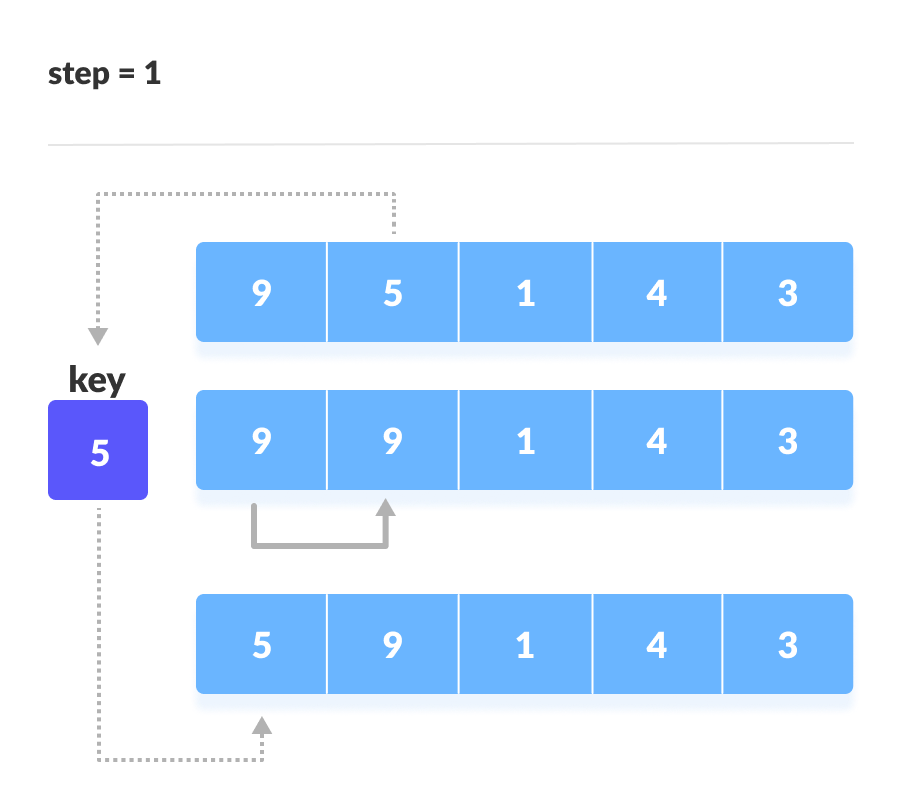
Bước 1: Chèn phần tử đầu tiên của phần chưa được sắp xếp vào phần đã được sắp xếp.
- Lấy phần tử đầu tiên của phần chưa được sắp xếp, tức là phần tử ở vị trí 1.
- Duyệt từ phải sang trái trong phần đã được sắp xếp, di chuyển các phần tử lớn hơn phần tử đang xét sang phải một vị trí.
- Nếu gặp phần tử nhỏ hơn hoặc bằng phần tử đang xét, chèn phần tử đang xét vào vị trí đó.
- Sau bước này, phần đã được sắp xếp sẽ có 2 phần tử, phần chưa được sắp xếp sẽ bao gồm các phần tử từ vị trí 2 đến vị trí n-1.
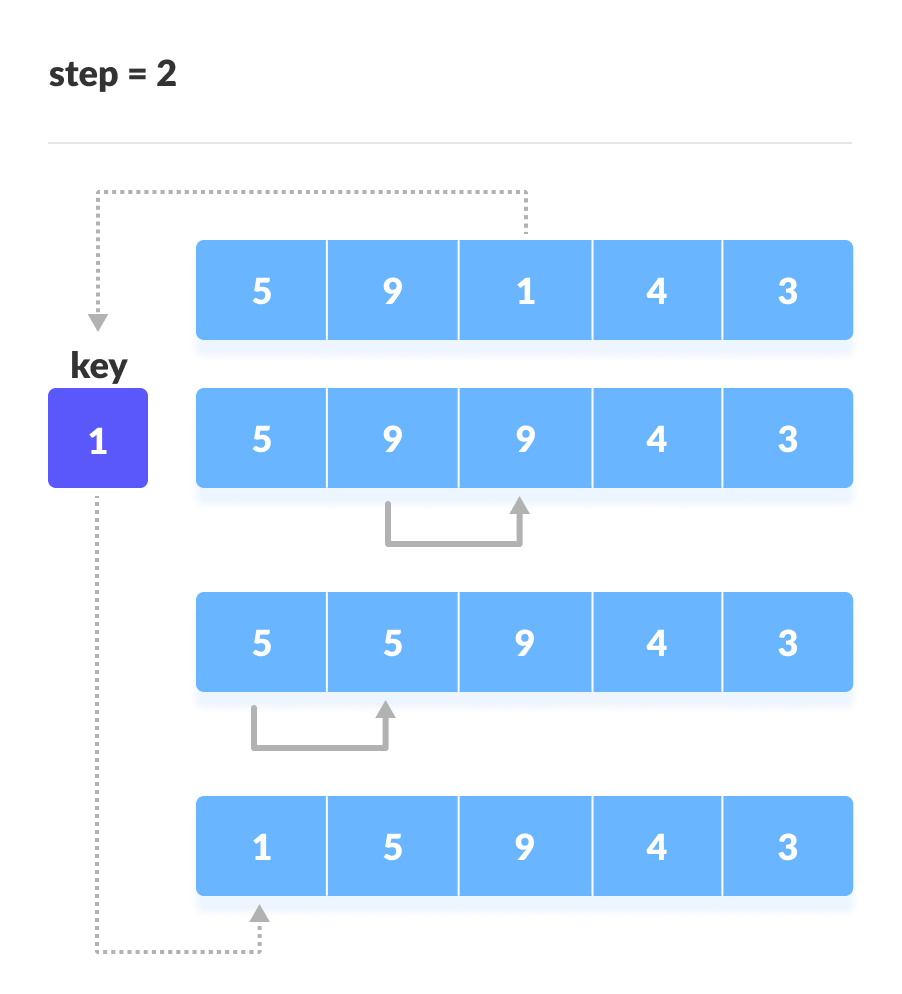
Bước 2: Chèn phần tử thứ hai của phần chưa được sắp xếp vào phần đã được sắp xếp.
- Lấy phần tử thứ hai của phần chưa được sắp xếp, tức là phần tử ở vị trí 2.
- Duyệt từ phải sang trái trong phần đã được sắp xếp, di chuyển các phần tử lớn hơn phần tử đang xét sang phải một vị trí.
- Nếu gặp phần tử nhỏ hơn hoặc bằng phần tử đang xét, chèn phần tử đang xét vào vị trí đó.
- Sau bước này, phần đã được sắp xếp sẽ có 3 phần tử, phần chưa được sắp xếp sẽ bao gồm các phần tử từ vị trí 3 đến vị trí n-1.
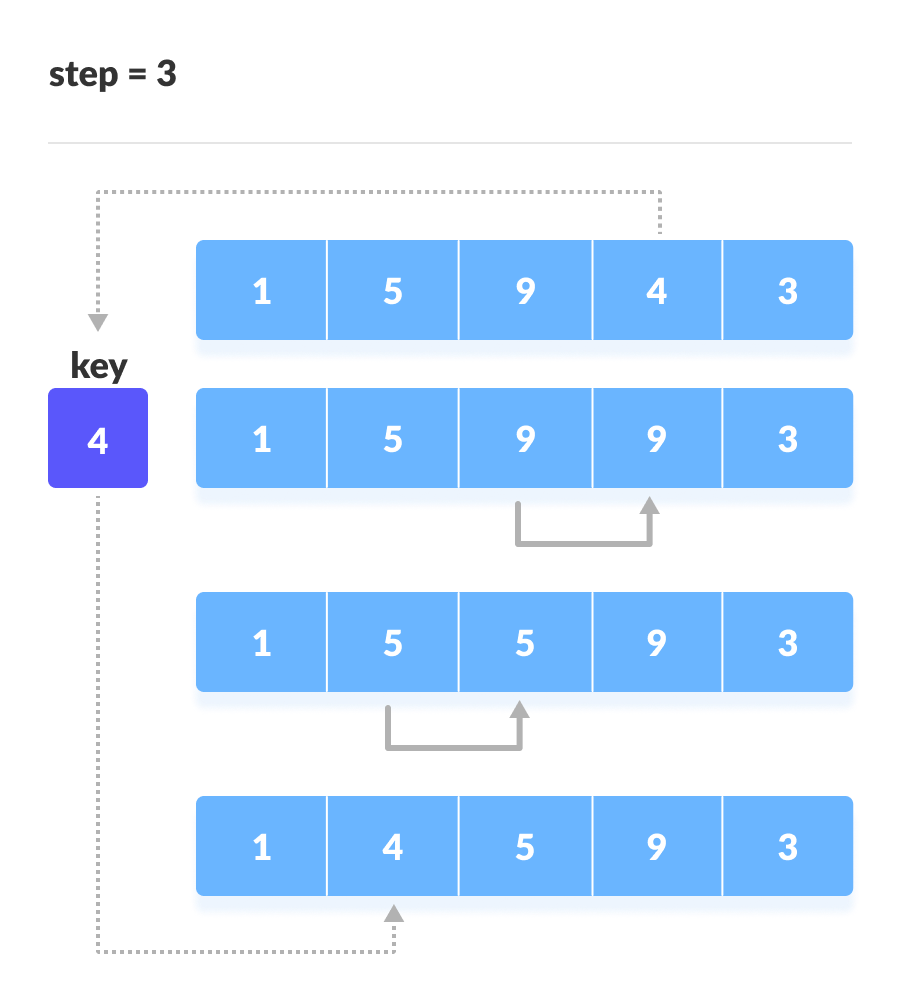
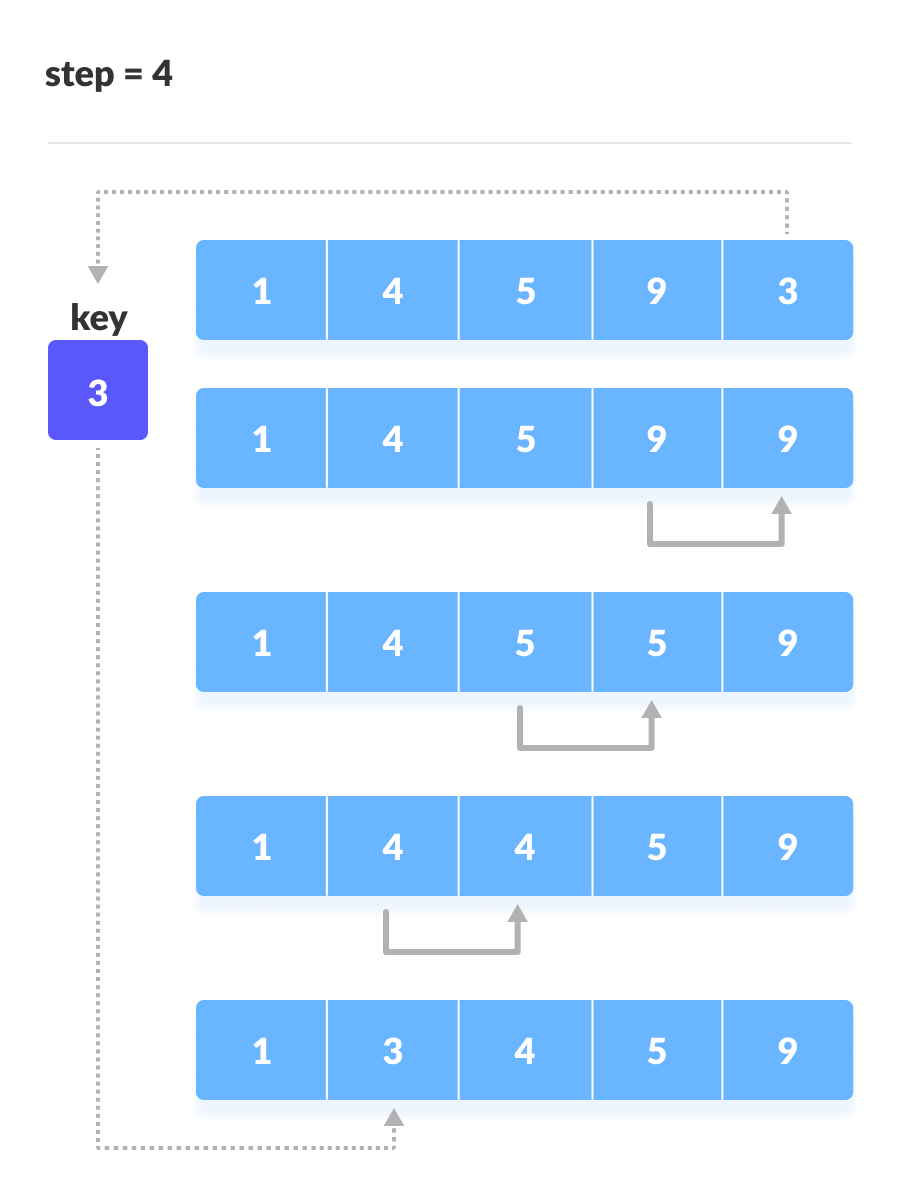
Tiếp tục lặp lại bước 2 cho đến khi tất cả các phần tử của phần chưa được sắp xếp được chèn vào phần đã được sắp xếp.

Chúng ta lấy ví dụ với mảng $[9, 5, 1, 4, 3]$ để minh họa toàn bộ quá trình sắp xếp chèn.

3. Cài đặt thuật toán sắp xếp chèn

class Solution:
    def insertionSort(self, nums: [int]) -> [int]:
        # Duyệt qua phần chưa được sắp xếp
        for i in range(1, len(nums)):
            temp = nums[i]
            j = i
            # Duyệt từ phải sang trái trong phần đã được sắp xếp
            while j > 0 and nums[j - 1] > temp:
                # Di chuyển các phần tử lớn hơn phần tử đang xét sang phải một vị trí
                nums[j] = nums[j - 1]
                j -= 1
            # Chèn phần tử đang xét vào vị trí thích hợp
            nums[j] = temp

        return nums

    def sortArray(self, nums: [int]) -> [int]:
        return self.insertionSort(nums)

4. Phân tích thuật toán sắp xếp chèn

Trường hợp tốt nhất: $O(n)$ . Trong trường hợp tốt nhất (khi mảng đã được sắp xếp tăng dần ban đầu), mỗi phần tử chỉ được so sánh với một phần tử khác và không cần di chuyển phần tử nào, do đó số lần so sánh là nhỏ nhất, bằng $∑^n_{i = 2}1 = n − 1$ .
Trường hợp xấu nhất: $O(n^2)$ . Trong trường hợp xấu nhất (khi mảng đã được sắp xếp giảm dần ban đầu), mỗi phần tử $nums[i]$ cần so sánh với $i - 1$ phần tử khác và di chuyển $i - 1$ phần tử, tổng số lần so sánh là lớn nhất, bằng $∑^n_{i=2}(i − 1) = \frac{n(n−1)}{2}$ .
Trường hợp trung bình: $O(n^2)$ . Nếu mảng ban đầu là ngẫu nhiên, tức là mỗi trường hợp xảy ra có cùng xác suất, ta có thể lấy trung bình của trường hợp tốt nhất và trường hợp xấu nhất, xấp xỉ $\frac{n^2}{4}$ . Do đó, độ phức tạp trung bình của thuật toán sắp xếp chèn là $O(n^2)$ .
Không gian bộ nhớ: $O(1)$ . Thuật toán sắp xếp chèn được thực hiện trực tiếp trên mảng ban đầu, chỉ sử dụng các biến con trỏ $i$ , $j$ và biến tham chiếu đến phần tử đầu tiên của phần chưa được sắp xếp.
Tính ổn định của thuật toán: Trong quá trình chèn, mỗi phần tử được chèn vào bên phải các phần tử bằng nhau, không làm thay đổi thứ tự tương đối của các phần tử bằng nhau. Do đó, thuật toán sắp xếp chèn là một thuật toán ổn định.