Bubble Sort

Sắp xếp nổi bọt

1. Ý tưởng thuật toán sắp xếp nổi bọt

Sắp xếp nổi bọt (Bubble Sort) cơ bản:
Qua nhiều lần lặp, thông qua việc so sánh và hoán đổi giữa các phần tử kề nhau, các phần tử có giá trị nhỏ hơn dần được di chuyển từ phía sau lên phía trước, các phần tử có giá trị lớn hơn dần được di chuyển từ phía trước xuống phía sau.

Quá trình này giống như các bọt khí từ đáy nước nổi lên mặt nước, đó cũng là nguồn gốc của tên gọi "Bubble Sort".

Tiếp theo, chúng ta sẽ sử dụng phương pháp "nổi bọt" để mô phỏng quá trình này.

Đầu tiên, hãy tưởng tượng mảng là một hàng "bọt", giá trị của các phần tử tương ứng với kích thước của bọt.
Sau đó, so sánh lần lượt từ trái sang phải giữa các cặp "bọt" liền kề:
1. Nếu "bọt" bên trái lớn hơn "bọt" bên phải, hoán đổi vị trí của hai "bọt".
2. Nếu "bọt" bên trái nhỏ hơn hoặc bằng "bọt" bên phải, hai "bọt" giữ nguyên vị trí.
Sau khi hoàn thành lần lặp này, "bọt" lớn nhất sẽ được đặt ở vị trí cuối cùng của tất cả các "bọt", giống như "bọt" từ đáy nổi lên mặt nước.

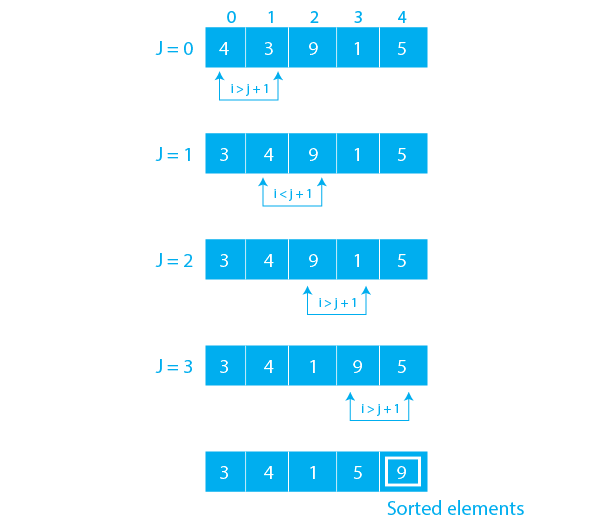
2. Bước thực hiện thuật toán sắp xếp nổi bọt

Giả sử mảng có $n$ phần tử, các bước thực hiện thuật toán sắp xếp nổi bọt như sau:

Bước $1$ $1$ "nổi bọt": Thực hiện "nổi bọt" cho $n$ $n$ phần tử đầu tiên, để đặt phần tử có giá trị lớn nhất ở vị trí đúng.
1. So sánh phần tử thứ $1$ với phần tử thứ $2$ trong mảng, nếu phần tử bên trái lớn hơn phần tử bên phải, hoán đổi vị trí của hai phần tử, ngược lại không hoán đổi.
2. Tiếp theo, so sánh phần tử thứ $2$ với phần tử thứ $3$ , nếu phần tử bên trái lớn hơn phần tử bên phải, hoán đổi vị trí của hai phần tử, ngược lại không hoán đổi.
3. Tiếp tục như vậy, cho đến khi so sánh phần tử thứ $n-1$ với phần tử thứ $n$ (hoặc hoán đổi) kết thúc.
4. Sau bước $1$ "nổi bọt", phần tử có giá trị lớn nhất trong $n$ phần tử đầu tiên sẽ được đặt ở vị trí cuối cùng.
Bước $2$ $2$ "nổi bọt": Thực hiện "nổi bọt" cho $n-1$ $n - 1$ phần tử đầu tiên, để đặt phần tử có giá trị lớn thứ hai ở vị trí đúng.
1. So sánh phần tử thứ $1$ với phần tử thứ $2$ trong mảng, nếu phần tử bên trái lớn hơn phần tử bên phải, hoán đổi vị trí của hai phần tử, ngược lại không hoán đổi.
2. Tiếp theo, so sánh phần tử thứ $2$ với phần tử thứ $3$ , nếu phần tử bên trái lớn hơn phần tử bên phải, hoán đổi vị trí của hai phần tử, ngược lại không hoán đổi.
3. Tiếp tục như vậy, cho đến khi so sánh phần tử thứ $n-2$ với phần tử thứ $n-1$ (hoặc hoán đổi) kết thúc. Tuy nhiên, khi chỉ còn $2$ phần tử, không cần so sánh nữa.
4. Sau bước $2$ "nổi bọt", phần tử có giá trị lớn thứ hai trong $n$ phần tử đầu tiên sẽ được đặt ở vị trí cuối cùng.
Tiếp tục như vậy, lặp lại quá trình "nổi bọt" cho đến khi không có hoán đổi vị trí nào xảy ra trong quá trình lặp, thì quá trình sắp xếp kết thúc.

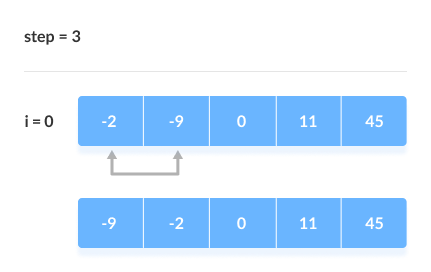
Chúng ta lấy ví dụ với mảng $[-2, 45, 0, 11, -9]$ , để mô phỏng toàn bộ quá trình sắp xếp nổi bọt.

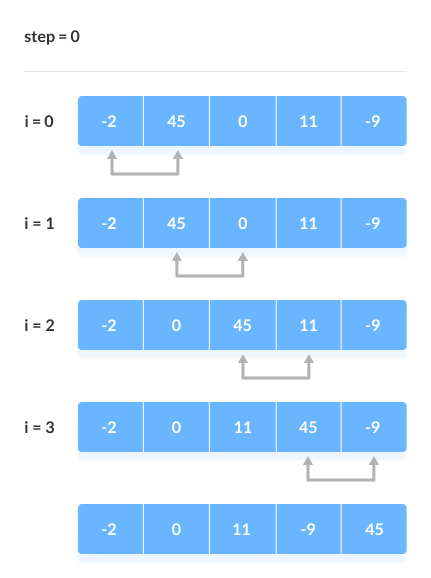
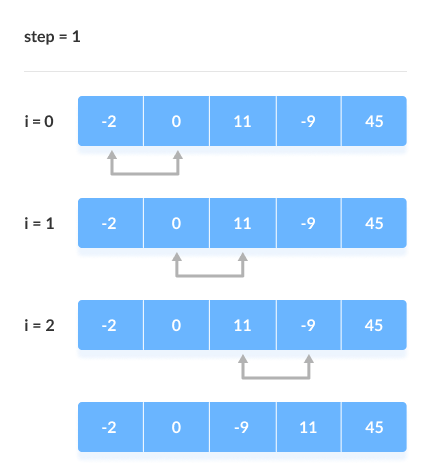
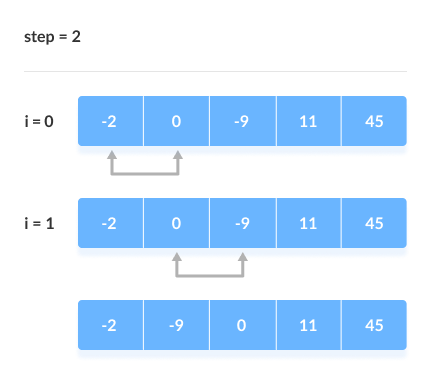
3. Cài đặt mã sắp xếp nổi bọt

class Solution:
    def bubbleSort(self, nums: [int]) -> [int]:
        # Bước "nổi bọt" thứ i
        for i in range(len(nums) - 1):
            flag = False    # Cờ hiệu xem có hoán đổi vị trí không
            # So sánh các cặp phần tử kề nhau từ phần tử thứ 1 đến phần tử thứ n - i + 1
            for j in range(len(nums) - i - 1):
                # So sánh cặp phần tử kề nhau, nếu phần tử bên trái lớn hơn phần tử bên phải, hoán đổi vị trí
                if nums[j] > nums[j + 1]:
                    nums[j], nums[j + 1] = nums[j + 1], nums[j]
                    flag = True
            if not flag:    # Nếu không có hoán đổi phần tử nào trong lần lặp này, thoát khỏi vòng lặp
                break
        
        return nums
    
    def sortArray(self, nums: [int]) -> [int]:
        return self.bubbleSort(nums)

4. Phân tích thuật toán sắp xếp nổi bọt

Độ phức tạp thời gian tốt nhất: $O(n)$ . Trong trường hợp tốt nhất (khi mảng đã được sắp xếp tăng dần ban đầu), chỉ cần $1$ lần lặp, tổng cộng thực hiện $n$ lần so sánh giữa các phần tử và không di chuyển phần tử nào, thuật toán có thể kết thúc. Do đó, độ phức tạp thời gian tốt nhất của thuật toán sắp xếp nổi bọt là $O(n)$ .
Độ phức tạp thời gian xấu nhất: $O(n^2)$ . Trong trường hợp xấu nhất (khi mảng đã được sắp xếp giảm dần ban đầu hoặc phần tử nhỏ nhất nằm ở cuối mảng), cần thực hiện $n$ lần lặp, tổng cộng thực hiện $∑^n_{i=2}(i−1) = \frac{n(n−1)}{2}$ lần so sánh giữa các phần tử. Do đó, độ phức tạp thời gian xấu nhất của thuật toán sắp xếp nổi bọt là $O(n^2)$ .
Độ phức tạp không gian: $O(1)$ . Thuật toán sắp xếp nổi bọt là thuật toán sắp xếp trên chính mảng ban đầu, chỉ sử dụng các biến con trỏ $i$ , $j$ và cờ hiệu $flag$ tương ứng với các biến hằng số.
Tính ứng dụng của thuật toán sắp xếp nổi bọt: Phương pháp sắp xếp nổi bọt thường di chuyển phần tử nhiều lần trong quá trình sắp xếp và hiệu suất thời gian của nó khá thấp. Do đó, phương pháp sắp xếp nổi bọt thích hợp cho các trường hợp dữ liệu đầu vào có kích thước nhỏ, đặc biệt là khi trạng thái ban đầu của dãy đã gần như được sắp xếp.
Tính ổn định của thuật toán sắp xếp nổi bọt: Vì các phần tử được hoán đổi chỉ nằm giữa các phần tử kề nhau, không làm thay đổi thứ tự tương đối của các phần tử bằng nhau, do đó, thuật toán sắp xếp nổi bọt là một thuật toán sắp xếp ổn định.