Counting Sort
About 4 min
Sắp xếp đếm
1. Ý tưởng của thuật toán sắp xếp đếm
Thuật toán sắp xếp đếm (Counting Sort):
Đếm số lần xuất hiện của mỗi phần tử trong mảng và sắp xếp các phần tử dựa trên thông tin đếm này để đặt chúng vào vị trí đúng, từ đó thực hiện việc sắp xếp.
2. Các bước của thuật toán sắp xếp đếm
- Xác định phạm vi sắp xếp: Duyệt qua mảng và tìm phần tử lớn nhất và phần tử nhỏ nhất trong mảng, tính phạm vi sắp xếp là .
- Định nghĩa mảng đếm: Định nghĩa một mảng đếm có kích thước bằng phạm vi sắp xếp, dùng để đếm số lần xuất hiện của mỗi phần tử. Trong đó:
- Chỉ số của mảng đại diện cho giá trị của phần tử là .
- Giá trị của mảng đại diện cho số lần xuất hiện của phần tử .
- Thống kê số lần xuất hiện của các phần tử trong mảng: Duyệt qua mảng và thống kê số lần xuất hiện của mỗi phần tử trong mảng đếm bằng cách tăng giá trị của mảng đếm tại chỉ số tương ứng, tức là tăng cho .
- Tạo mảng đếm tích lũy: Bắt đầu từ phần tử thứ của mảng đếm, tính tổng tích lũy của mỗi phần tử với phần tử trước đó. Lúc này, đại diện cho vị trí cuối cùng mà phần tử có giá trị xuất hiện trong mảng sắp xếp.
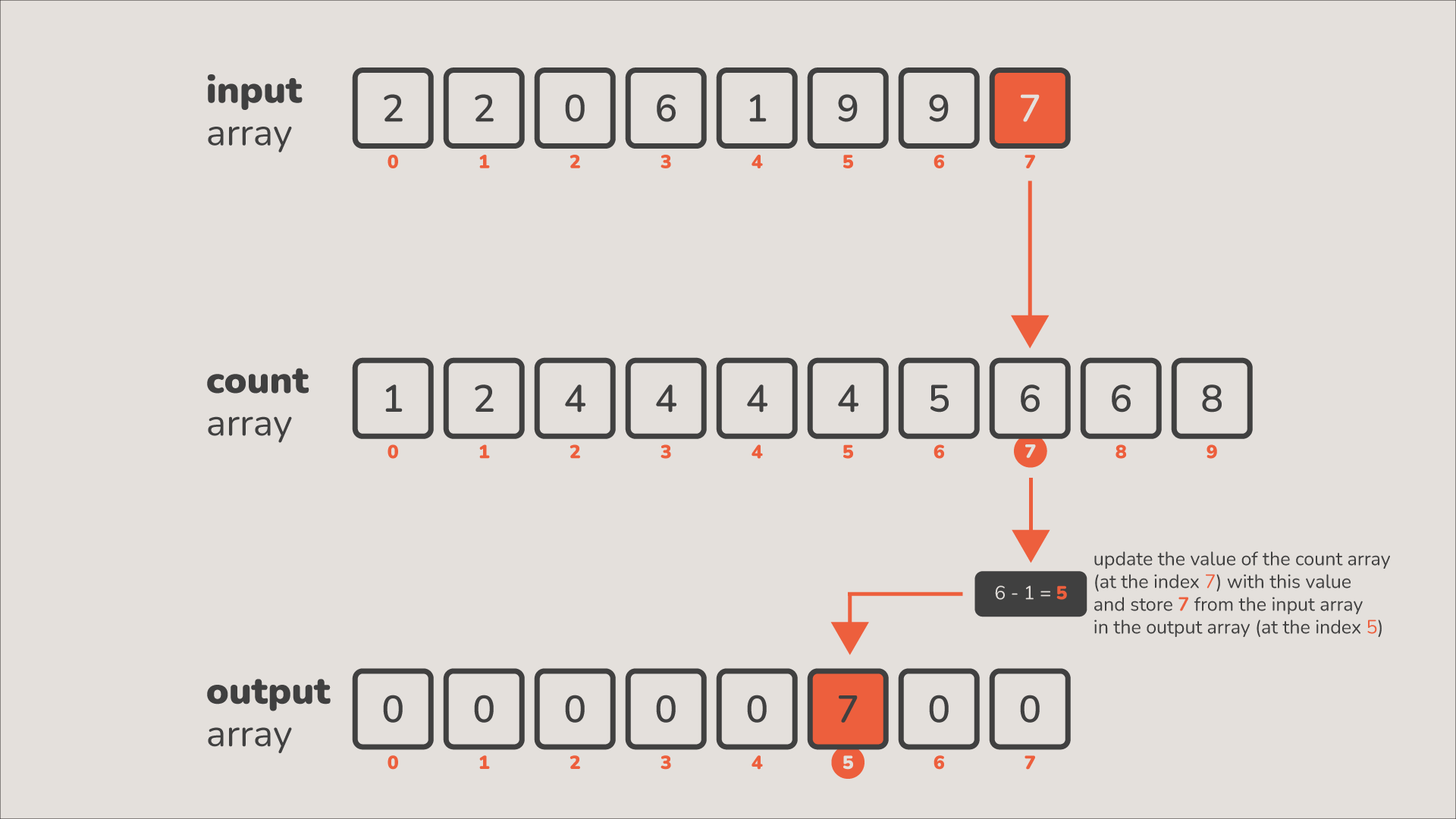
- Điền ngược vào mảng kết quả: Duyệt qua mảng theo thứ tự ngược, điền từng phần tử vào vị trí đúng.
- Điền phần tử vào vị trí trong mảng kết quả .
- Sau khi điền, giảm giá trị tại chỉ số tương ứng trong mảng tích lũy đếm đi , từ đó tìm vị trí để đặt phần tử tiếp theo.
Chúng ta lấy ví dụ với mảng để minh họa toàn bộ quá trình sắp xếp đếm.
3. Cài đặt thuật toán sắp xếp đếm
class Solution:
def countingSort(self, nums: [int]) -> [int]:
# Tìm phần tử lớn nhất và nhỏ nhất trong mảng
nums_min, nums_max = min(nums), max(nums)
# Định nghĩa mảng đếm counts, kích thước bằng phạm vi sắp xếp
size = nums_max - nums_min + 1
counts = [0 for _ in range(size)]
# Thống kê số lần xuất hiện của phần tử num
for num in nums:
counts[num - nums_min] += 1
# Tạo mảng đếm tích lũy
for i in range(1, size):
counts[i] += counts[i - 1]
# Điền ngược vào mảng kết quả
res = [0 for _ in range(len(nums))]
for i in range(len(nums) - 1, -1, -1):
num = nums[i]
# Dựa vào mảng tích lũy đếm, đặt num vào vị trí tương ứng trong mảng
res[counts[num - nums_min] - 1] = num
# Giảm giá trị tại vị trí tương ứng trong mảng tích lũy đếm đi 1, để tìm vị trí đặt phần tử num tiếp theo
counts[nums[i] - nums_min] -= 1
return res
def sortArray(self, nums: [int]) -> [int]:
return self.countingSort(nums)4. Phân tích thuật toán sắp xếp đếm
- Độ phức tạp thời gian: . Trong đó là giá trị phạm vi của mảng đầu vào.
- Độ phức tạp không gian: . Trong đó là giá trị phạm vi của mảng đầu vào. Vì độ dài của mảng đếm phụ thuộc vào phạm vi dữ liệu trong mảng đầu vào (bằng với sự khác biệt giữa giá trị lớn nhất và nhỏ nhất trong mảng đầu vào cộng thêm ). Do đó, thuật toán sắp xếp đếm yêu cầu một lượng lớn bộ nhớ đối với các mảng có phạm vi dữ liệu lớn.
- Ứng dụng của thuật toán sắp xếp đếm: Thuật toán sắp xếp đếm thường được sử dụng cho việc sắp xếp các số nguyên, không phù hợp cho việc sắp xếp theo thứ tự chữ cái hoặc theo tên người.
- Tính ổn định của thuật toán: Do việc điền các phần tử vào mảng kết quả được thực hiện theo thứ tự ngược, giúp tránh thay đổi thứ tự tương đối giữa các phần tử bằng nhau. Do đó, thuật toán sắp xếp đếm là một thuật toán ổn định.