LeetCode 0375
0375. Guess Number Higher or Lower II
- Thẻ: Toán học, Quy hoạch động, Trò chơi
- Độ khó: Trung bình
Tóm tắt bài toán
Mô tả: Bây giờ có hai người đang chơi một trò chơi đoán số, quy tắc trò chơi như sau:
- Đối tác chọn một số từ .
- Chúng ta cố gắng đoán số mà đối tác đã chọn.
- Nếu chúng ta đoán đúng số, chúng ta sẽ thắng trò chơi.
- Nếu chúng ta đoán sai, đối tác sẽ cho chúng ta biết số đã chọn lớn hơn hoặc nhỏ hơn số chúng ta đoán và chúng ta cần tiếp tục đoán số.
- Mỗi khi chúng ta đoán số và đoán sai, chúng ta phải trả một khoản tiền là . Nếu chúng ta hết tiền, chúng ta sẽ thua trò chơi.
Giờ đây, cho một số nguyên cụ thể .
Yêu cầu: Hãy trả về số tiền tối thiểu mà chúng ta cần trả (bất kể đối tác chọn số nào) để đảm bảo chúng ta thắng trò chơi.
Giải thích:
- .
Ví dụ:
- Ví dụ 1:
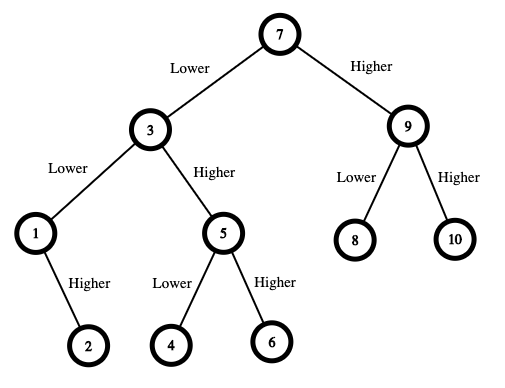
Input: n = 10
Output: 16
Giải thích: Chiến lược chiến thắng như sau:
- Khoảng số là từ [1,10]. Bạn đoán số 7 đầu tiên.
- Nếu đó là số tôi đã chọn, tổng chi phí của bạn là $0. Nếu không, bạn phải trả $7.
- Nếu số của tôi lớn hơn, bước tiếp theo bạn cần đoán số trong khoảng [8, 10]. Bạn có thể đoán số 9.
- Nếu đó là số tôi đã chọn, tổng chi phí của bạn là $7. Nếu không, bạn phải trả $9.
- Nếu số của tôi lớn hơn, số đó chắc chắn là 10. Bạn đoán số 10 và thắng trò chơi, tổng chi phí của bạn là $7 + $9 = $16.
- Nếu số của tôi nhỏ hơn, số đó chắc chắn là 8. Bạn đoán số 8 và thắng trò chơi, tổng chi phí của bạn là $7 + $9 = $16.
- Nếu số của tôi nhỏ hơn, bước tiếp theo bạn cần đoán số trong khoảng [1, 6]. Bạn có thể đoán số 3.
- Nếu đó là số tôi đã chọn, tổng chi phí của bạn là $7. Nếu không, bạn phải trả $3.
- Nếu số của tôi lớn hơn, bước tiếp theo bạn cần đoán số trong khoảng [4, 6]. Bạn có thể đoán số 5.
- Nếu đó là số tôi đã chọn, tổng chi phí của bạn là $7 + $3 = $10. Nếu không, bạn phải trả $5.
- Nếu số của tôi lớn hơn, số đó chắc chắn là 6. Bạn đoán số 6 và thắng trò chơi, tổng chi phí của bạn là $7 + $3 + $5 = $15.
- Nếu số của tôi nhỏ hơn, số đó chắc chắn là 4. Bạn đoán số 4 và thắng trò chơi, tổng chi phí của bạn là $7 + $3 + $5 = $15.
- Nếu số của tôi nhỏ hơn, bước tiếp theo bạn cần đoán số trong khoảng [1, 2]. Bạn có thể đoán số 1.
- Nếu đó là số tôi đã chọn, tổng chi phí của bạn là $7 + $3 = $10. Nếu không, bạn phải trả $1.
- Nếu số của tôi lớn hơn, số đó chắc chắn là 2. Bạn đoán số 2 và thắng trò chơi, tổng chi phí của bạn là $7 + $3 + $1 = $11.
Trong trường hợp xấu nhất, bạn phải trả $16. Vì vậy, bạn chỉ cần $16 để đảm bảo thắng trò chơi.- Ví dụ 2:
Input: n = 2
Output: 1
Giải thích: Có hai số có thể là 1 và 2.
- Bạn có thể đoán 1 đầu tiên.
- Nếu đó là số tôi đã chọn, tổng chi phí của bạn là $0. Nếu không, bạn phải trả $1.
- Nếu số của tôi lớn hơn, số đó chắc chắn là 2. Bạn đoán số 2 và thắng trò chơi, tổng chi phí của bạn là $1.
Trong trường hợp xấu nhất, bạn phải trả $1.Ý tưởng giải quyết
Ý tưởng 1: Quy hoạch động
Ban đầu, chúng ta có thể nghĩ rằng vấn đề này có thể được giải quyết bằng phương pháp tìm kiếm nhị phân, nhưng thực tế không phải như vậy.
Bởi vì chúng ta có thể tìm ra số lần đoán tối thiểu để đoán đúng, nhưng số tiền tối thiểu cần trả cho số lần đoán tối thiểu đó không phải là số tiền tối thiểu.
Nghĩa là, chiến lược tìm kiếm nhị phân không thể tìm ra số tiền tối thiểu cần trả để đảm bảo chúng ta thắng.
Vì vậy, chúng ta cần phải thay đổi cách suy nghĩ.
Chúng ta có thể suy nghĩ theo cách đệ quy.
Với mỗi số từ đến :
- Nếu chính xác là số đúng, chúng ta sẽ thắng và không cần trả bất kỳ số tiền nào.
- Nếu không phải là số đúng, chúng ta sẽ phải trả số tiền là , và chúng ta sẽ biết rằng số đúng lớn hơn hoặc nhỏ hơn số chúng ta đoán và chúng ta cần tiếp tục đoán.
- Nếu số đúng nhỏ hơn số chúng ta đoán, chúng ta chỉ cần tìm số tiền tối thiểu cần trả để đảm bảo chúng ta thắng trong khoảng từ đến , sau đó cộng thêm là số tiền tối thiểu cần trả để đảm bảo chúng ta thắng.
- Nếu số đúng lớn hơn số chúng ta đoán, chúng ta chỉ cần tìm số tiền tối thiểu cần trả để đảm bảo chúng ta thắng trong khoảng từ đến , sau đó cộng thêm là số tiền tối thiểu cần trả để đảm bảo chúng ta thắng.
- Vì số đúng có thể nhỏ hơn hoặc lớn hơn số chúng ta đoán, chúng ta cần chuẩn bị số tiền tối thiểu cho cả hai trường hợp, và sau đó chọn số tiền tối thiểu lớn nhất trong hai trường hợp đó, sau đó cộng thêm .
Chúng ta có thể duyệt qua từng số , tính toán số tiền tối thiểu cần trả cho mỗi trường hợp và chọn số tiền tối thiểu lớn nhất là kết quả cuối cùng.
Chúng ta có thể định nghĩa một hàm để biểu diễn số tiền tối thiểu cần trả để đảm bảo chúng ta thắng, sau đó có thể có công thức đệ quy: .
Áp dụng công thức đệ quy vào , ta có: .
Tiếp theo chúng ta có thể giải quyết bài toán này bằng phương pháp quy hoạch động.
1. Phân chia giai đoạn
Phân chia giai đoạn theo độ dài của khoảng.
2. Định nghĩa trạng thái
Định nghĩa trạng thái là: số tiền tối thiểu cần trả để đảm bảo chúng ta thắng trong khoảng số từ đến .
3. Công thức chuyển tiếp
.
4. Điều kiện ban đầu
- Mặc định số tiền tối thiểu cần trả để đảm bảo chúng ta thắng trong khoảng số từ đến là vô cùng lớn.
- Khi độ dài khoảng là , tức là khoảng chỉ có số, chắc chắn là số đúng, vì vậy số tiền tối thiểu cần trả là , tức là .
5. Kết quả cuối cùng
Dựa trên trạng thái đã định nghĩa trước đó, là: số tiền tối thiểu cần trả để đảm bảo chúng ta thắng trong khoảng số từ đến . Vậy kết quả cuối cùng là .
Ý tưởng 1: Code
class Solution:
def getMoneyAmount(self, n: int) -> int:
dp = [[0] * (n + 2) for _ in range(n + 2)]
for l in range(2, n + 1):
for i in range(1, n + 2 - l):
j = i + l - 1
dp[i][j] = float('inf')
for k in range(i, j):
dp[i][j] = min(dp[i][j], max(dp[i][k - 1], dp[k + 1][j]) + k)
return dp[1][n]Ý tưởng 1: Phân tích độ phức tạp
- Độ phức tạp thời gian: , trong đó là số nguyên đã cho.
- Độ phức tạp không gian: .