KMP

1. Giới thiệu thuật toán KMP

Thuật toán KMP: Tên đầy đủ là "Knuth Morris Pratt Algorithm", được đặt theo tên của ba nhà phát minh là Donald Knuth, James H. Morris và Vaughan Pratt. Thuật toán KMP được ba người này công bố vào năm 1977.
Ý tưởng của thuật toán KMP: Đối với văn bản T và mẫu p đã cho, khi gặp một ký tự trong văn bản T không khớp với mẫu p, chúng ta có thể sử dụng thông tin từ sự không khớp để giảm số lần so sánh giữa mẫu p và văn bản T, tránh việc quay lại vị trí trước đó trong văn bản, nhằm đạt được mục tiêu tìm kiếm nhanh chóng.

1.1 Nhược điểm của thuật toán so sánh đơn giản

Trong quá trình so sánh đơn giản, chúng ta sử dụng hai con trỏ i và j để chỉ định các ký tự hiện tại đang được so sánh trong văn bản T và mẫu p. Khi gặp một ký tự trong văn bản T không khớp với mẫu p, con trỏ j quay lại vị trí ban đầu, con trỏ i quay lại vị trí bắt đầu so sánh trước đó, sau đó bắt đầu một vòng lặp so sánh mới, như hình minh họa dưới đây.

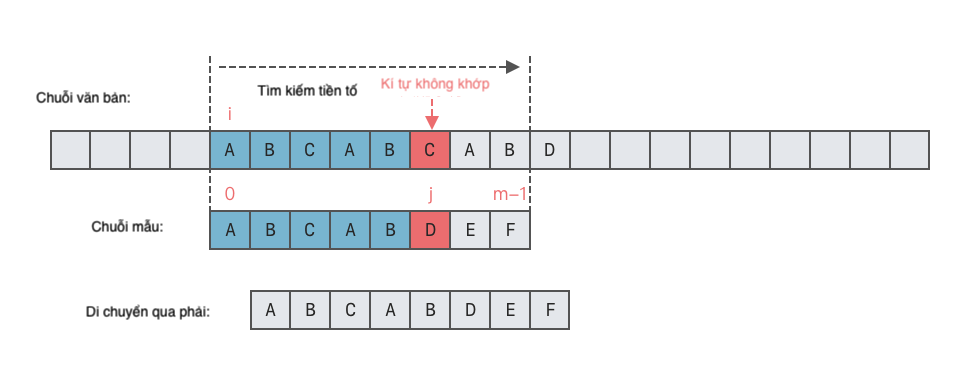
Như vậy, trong thuật toán Brute Force, nếu quá trình so sánh từ vị trí T[i] bắt đầu thất bại, thuật toán sẽ ngay lập tức thử so sánh từ vị trí T[i + 1]. Nếu i đã so sánh đến vị trí cuối cùng, thì thao tác này tương đương với việc quay lại vị trí ban đầu của con trỏ i.

Vậy có thuật toán nào mà cho phép i không quay lại, mà tiếp tục di chuyển sang phải không?

1.2 Cải tiến của thuật toán KMP

Nếu chúng ta có thể thu được một số "thông tin" từ mỗi lần không khớp và thông tin này có thể giúp chúng ta bỏ qua các vị trí không thể khớp thành công, thì chúng ta có thể giảm đáng kể số lần so sánh giữa mẫu p và văn bản T, từ đó đạt được mục tiêu tìm kiếm nhanh chóng.

Mỗi lần không khớp cung cấp cho chúng ta thông tin: Một chuỗi con của văn bản chính xác bằng một tiền tố của mẫu.

Ý nghĩa của thông tin này là: Nếu một chuỗi con của văn bản T[i: i + m] không khớp với mẫu p, thì chuỗi con của văn bản T bắt đầu từ vị trí i và liên tiếp j - 1 ký tự sau đó sẽ chính xác giống với j - 1 ký tự đầu của mẫu p, tức là T[i: i + j] == p[0: j].

Nhưng thông tin này có tác dụng gì?

Ví dụ về ví dụ trong phần trước, chuỗi con của văn bản T bắt đầu từ vị trí i và liên tiếp 5 ký tự sẽ chính xác giống với 5 ký tự đầu của mẫu p, tức là "ABCAB" == "ABCAB". Dựa trên thông tin này, chúng ta có thể suy ra: Chuỗi con của văn bản T bắt đầu từ vị trí i + 3 và liên tiếp 2 ký tự sẽ chính xác giống với 2 ký tự cuối của mẫu p, tức là T[i + 3: i + 5] == p[0: 2] và phần này (màu xanh dương trong hình dưới đây) đã được so sánh trước đó, không cần so sánh lại, có thể bỏ qua.

Vì vậy, chúng ta có thể đặt T[i + 5] trên văn bản trực tiếp vào vị trí p[2] trên mẫu và tiếp tục so sánh. Lúc này, i không cần phải quay lại, có thể di chuyển tiếp sang phải. Trong quá trình này, chúng ta chỉ cần đặt lại con trỏ j của mẫu.

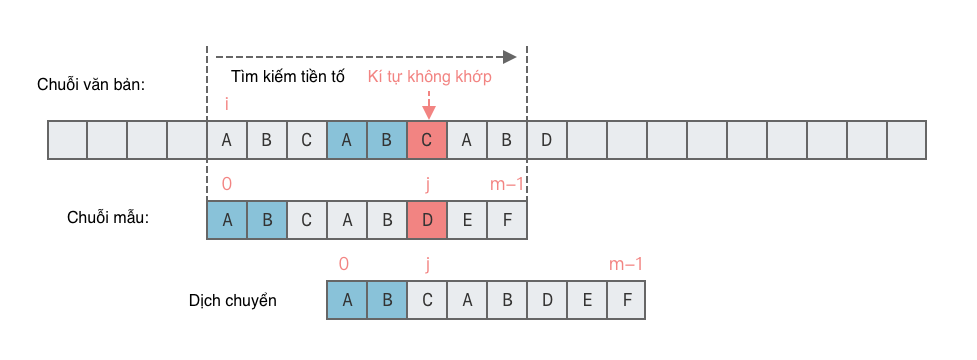
Thuật toán KMP sử dụng ý tưởng này và đã tiền xử lý mẫu p, tính toán một "bảng phần tử khớp", được lưu trữ trong một mảng next. Sau đó, khi mỗi lần không khớp xảy ra, không quay lại con trỏ i của văn bản, mà quyết định số lượng ký tự mà mẫu có thể di chuyển sang phải dựa trên giá trị của next[j - 1], tức là số lượng ký tự mà mẫu có thể di chuyển sang phải.

Ví dụ, trong ví dụ trước đó, khi mẫu p không khớp ở vị trí j = 5, chúng ta không cần quay lại con trỏ i của văn bản, mà chúng ta di chuyển con trỏ j sang vị trí 2 dựa trên giá trị next[4] = 2, để T[i + 5] trực tiếp trùng với p[2], sau đó tiếp tục so sánh, như hình dưới đây.

1.3 Mảng next

Trong phần trước đã đề cập đến "bảng so khớp một phần", còn được gọi là "bảng tiền tố", được sử dụng trong thuật toán KMP và được lưu trữ trong mảng next. next[j] biểu thị ý nghĩa là: ghi lại độ dài của tiền tố và hậu tố dài nhất trong chuỗi mẫu p cho đến vị trí j (bao gồm j).

Đơn giản mà nói, nó là để tìm: "độ dài k lớn nhất" trong chuỗi con p[0: j + 1] của chuỗi mẫu p, sao cho "ký tự đầu tiên" chính xác bằng "ký tự cuối cùng". Tất nhiên, chuỗi con p[0: j + 1] không tham gia so sánh.

Hãy xem một ví dụ để giải thích, lấy ví dụ p = "ABCABCD".

next[0] = 0, vì "A" không có tiền tố và hậu tố giống nhau, độ dài lớn nhất là 0.
next[1] = 0, vì "AB" không có tiền tố và hậu tố giống nhau, độ dài lớn nhất là 0.
next[2] = 0, vì "ABC" không có tiền tố và hậu tố giống nhau, độ dài lớn nhất là 0.
next[3] = 1, vì "ABCA" có tiền tố và hậu tố giống nhau là "a", độ dài lớn nhất là 1.
next[4] = 2, vì "ABCAB" có tiền tố và hậu tố giống nhau là "AB", độ dài lớn nhất là 2.
next[5] = 3, vì "ABCABC" có tiền tố và hậu tố giống nhau là "ABC", độ dài lớn nhất là 3.
next[6] = 0, vì "ABCABCD" không có tiền tố và hậu tố giống nhau, độ dài lớn nhất là 0.

Tương tự, ta có bảng tiền tố của chuỗi "ABCABDEF" là [0, 0, 0, 1, 2, 0, 0, 0]. Bảng tiền tố của chuỗi "AABAAAB" là [0, 1, 0, 1, 2, 2, 3]. Bảng tiền tố của chuỗi "ABCDABD" là [0, 0, 0, 0, 1, 2, 0].

Trong ví dụ trước, khi không khớp giữa p[5] và T[i + 5], dựa vào giá trị của vị trí trước đó của chuỗi mẫu tại vị trí không khớp j, tức là next[4] = 2, chúng ta di chuyển trực tiếp T[i + 5] để trùng khớp với p[2], sau đó tiếp tục so sánh, như hình ảnh dưới đây.

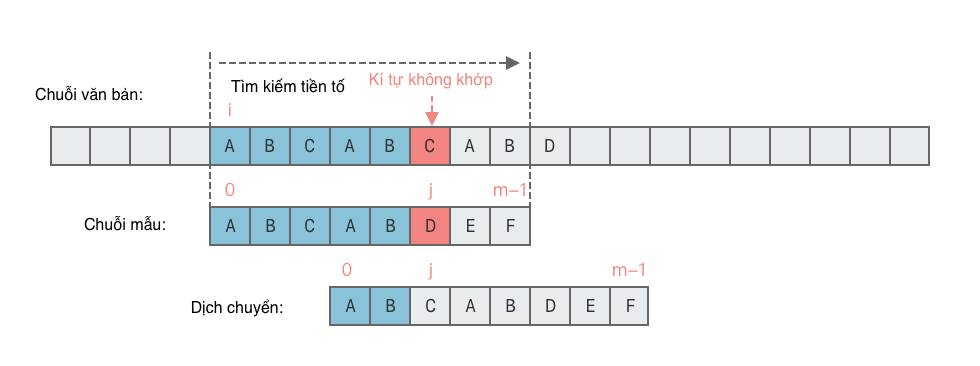
Nhưng nguyên lý di chuyển như vậy là gì?

Thực tế, trong ví dụ đã đề cập ở phần "1.2 Cải tiến của thuật toán KMP", chúng ta đã đề cập đến điều này. Bây giờ chúng ta sẽ tổng kết và mở rộng quy luật này, thực sự quá trình này chính là sử dụng bảng tiền tố để di chuyển chuỗi mẫu, và kết luận cụ thể như sau.

Nếu không khớp giữa chuỗi văn bản T[i: i + m] và chuỗi mẫu p xảy ra tại vị trí thứ j, thì:

j ký tự liên tiếp trong chuỗi văn bản T kể từ vị trí i chắc chắn giống với j ký tự đầu tiên của chuỗi mẫu p, tức là: T[i: i + j] == p[0: j].
Nếu k ký tự đầu tiên của chuỗi mẫu p giống với k ký tự cuối cùng của chuỗi mẫu p, tức là p[0: k] == p[j - k: j], và k càng lớn càng tốt.

Kết luận là: chuỗi con của chuỗi văn bản từ vị trí i + m - k đến i + m giống với p[0: k] (đây là phần đã so sánh), không cần so sánh lại, có thể bỏ qua.

Sau đó, chúng ta chỉ cần đặt ký tự T[i + m] của chuỗi văn bản vào vị trí p[k] của chuỗi mẫu và tiếp tục so sánh. Ở đây, k chính là next[j - 1].

2. Các bước của thuật toán KMP

2.1 Xây dựng mảng next

Chúng ta có thể xây dựng mảng next bằng cách sử dụng phương pháp đệ quy.

Chúng ta chia chuỗi mẫu p thành hai phần: left và right. left đại diện cho vị trí bắt đầu của tiền tố, right đại diện cho vị trí bắt đầu của hậu tố. Ban đầu, left = 0 và right = 1.
So sánh tiền tố và hậu tố để kiểm tra xem chúng có bằng nhau không. Sử dụng p[left] và p[right] để so sánh.
Nếu p[left] != p[right], điều đó có nghĩa là tiền tố và hậu tố hiện tại không giống nhau. Khi đó, giữ nguyên vị trí bắt đầu của hậu tố k, và di chuyển vị trí bắt đầu của tiền tố left về vị trí next[left - 1] cho đến khi p[left] == p[right].
Nếu p[left] == p[right], điều đó có nghĩa là tiền tố và hậu tố hiện tại giống nhau. Ta có thể tăng giá trị của left lên 1, lúc này left không chỉ là vị trí bắt đầu của tiền tố trong lần so sánh tiếp theo, mà còn là độ dài của tiền tố dài nhất hiện tại.
Ghi lại độ dài của tiền tố và hậu tố dài nhất trong chuỗi mẫu p cho đến vị trí right là left, tức là next[right] = left.

2.2 Các bước chính của thuật toán KMP

Xây dựng bảng tiền tố next dựa trên các bước đã mô tả ở trên.
Sử dụng hai con trỏ i và j, trong đó i chỉ vị trí hiện tại của chuỗi văn bản mà chúng ta đang so khớp, j chỉ vị trí hiện tại của chuỗi mẫu mà chúng ta đang so khớp. Ban đầu, i = 0 và j = 0.
Lặp lại quá trình kiểm tra xem tiền tố của chuỗi mẫu có khớp không. Nếu tiền tố của chuỗi mẫu không khớp, chúng ta sẽ di chuyển chuỗi mẫu về vị trí trước đó, tức là j = next[j - 1], cho đến khi j == 0 hoặc tiền tố khớp thành công thì dừng lại.
Nếu tiền tố của chuỗi mẫu khớp thành công, chúng ta sẽ di chuyển chuỗi mẫu sang phải 1 vị trí, tức là j += 1.
Nếu chuỗi mẫu khớp hoàn toàn, chúng ta sẽ trả về vị trí bắt đầu của chuỗi mẫu p trong chuỗi văn bản T, tức là i - j + 1.
Nếu chưa khớp hoàn toàn, chúng ta sẽ di chuyển chuỗi văn bản sang phải 1 vị trí, tức là i += 1, và tiếp tục so khớp.
Nếu chúng ta đã duyệt qua toàn bộ chuỗi văn bản mà không khớp hoàn toàn, điều đó có nghĩa là không tìm thấy chuỗi mẫu trong chuỗi văn bản, chúng ta sẽ trả về -1 để chỉ ra rằng không có sự khớp.

3. Cài đặt thuật toán KMP

# Tạo mảng next
# next[j] biểu thị độ dài của tiền tố và hậu tố dài nhất trong chuỗi mẫu p cho đến vị trí j
def generateNext(p: str):
    m = len(p)
    next = [0 for _ in range(m)]                # Khởi tạo tất cả các phần tử của mảng bằng 0
    
    left = 0                                    # left đại diện cho vị trí bắt đầu của tiền tố
    for right in range(1, m):                   # right đại diện cho vị trí bắt đầu của hậu tố
        while left > 0 and p[left] != p[right]: # Nếu không khớp, di chuyển left về trước, dừng khi left == 0
            left = next[left - 1]               # Di chuyển left về trước
        if p[left] == p[right]:                 # Nếu khớp, tăng left lên 1
            left += 1
        next[right] = left                      # Ghi lại độ dài của tiền tố, cập nhật next[right], tiếp tục vòng lặp, right += 1

    return next

# Thuật toán KMP, T là chuỗi văn bản, p là chuỗi mẫu
def kmp(T: str, p: str) -> int:
    n, m = len(T), len(p)
    
    next = generateNext(p)                      # Tạo mảng next
    
    j = 0                                       # j đại diện cho vị trí hiện tại của chuỗi mẫu
    for i in range(n):                          # i đại diện cho vị trí hiện tại của chuỗi văn bản
        while j > 0 and T[i] != p[j]:           # Nếu tiền tố của chuỗi mẫu không khớp, di chuyển chuỗi mẫu về trước, dừng khi j == 0
            j = next[j - 1]
        if T[i] == p[j]:                        # Nếu tiền tố của chuỗi mẫu khớp, tăng j lên 1 và tiếp tục so khớp
            j += 1
        if j == m:                              # Nếu chuỗi mẫu khớp hoàn toàn, trả về vị trí bắt đầu của khớp
            return i - j + 1
    return -1                                   # Nếu không khớp, trả về -1
            
print(kmp("abbcfdddbddcaddebc", "ABCABCD"))
print(kmp("abbcfdddbddcaddebc", "bcf"))
print(kmp("aaaaa", "bba"))
print(kmp("mississippi", "issi"))
print(kmp("ababbbbaaabbbaaa", "bbbb"))

4. Phân tích thuật toán KMP

Trong giai đoạn xây dựng bảng tiền tố, độ phức tạp thời gian của thuật toán KMP là $O(m)$ , trong đó $m$ là độ dài của chuỗi mẫu p.
Trong giai đoạn so khớp, thuật toán KMP điều chỉnh vị trí so khớp dựa trên bảng tiền tố, chỉ di chuyển con trỏ i của chuỗi văn bản và không quay lại. Do đó, độ phức tạp thời gian của giai đoạn so khớp là $O(n)$ , trong đó $n$ là độ dài của chuỗi văn bản T.
Vì vậy, độ phức tạp thời gian của toàn bộ thuật toán KMP là $O(n + m)$ , so với độ phức tạp thời gian $O(n * m)$ của thuật toán so khớp thông thường, thuật toán KMP có hiệu suất cao hơn rất nhiều.