Boyer Moore

1. Giới thiệu thuật toán Boyer Moore

Thuật toán Boyer Moore: Được viết tắt là BM, được đặt theo tên hai nhà phát minh Robert S. Boyer và J Strother Moore. Thuật toán BM là một thuật toán tìm kiếm chuỗi hiệu quả được đề xuất vào năm 1977. Trong thực tế, nó nhanh hơn thuật toán KMP khoảng 3-5 lần.
Ý tưởng của thuật toán BM: Với một chuỗi văn bản cho trước T và một chuỗi mẫu p, trước tiên ta tiền xử lý chuỗi mẫu p. Sau đó, trong quá trình khớp, khi phát hiện một ký tự trong chuỗi văn bản T không khớp với chuỗi mẫu p, dựa trên chiến lược khởi động, ta có thể di chuyển chuỗi mẫu sang phải một số vị trí tối đa để bỏ qua một số trường hợp không khớp.

Bản chất của thuật toán BM là sử dụng hai chiến lược khởi động khác nhau để tính toán số vị trí di chuyển sau: "Quy tắc ký tự không hợp lệ" và "Quy tắc di chuyển hậu tố tốt".

Quá trình tính toán hai chiến lược khởi động này chỉ liên quan đến chuỗi mẫu p, không liên quan đến chuỗi văn bản T. Do đó, khi tiền xử lý chuỗi mẫu p, ta có thể tạo trước "Bảng di chuyển theo quy tắc ký tự không hợp lệ" và "Bảng di chuyển theo quy tắc di chuyển hậu tố tốt", sau đó trong quá trình khớp, chỉ cần so sánh số lớn nhất của hai chiến lược này để di chuyển sau.

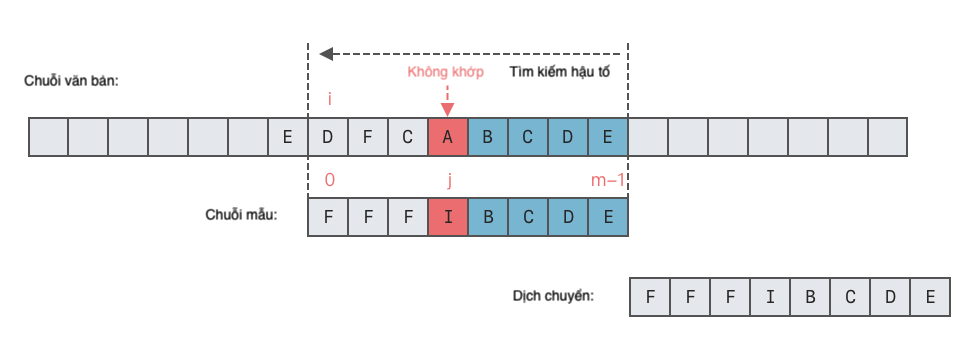
Đồng thời, cần lưu ý rằng trong quá trình di chuyển chuỗi mẫu, thuật toán BM di chuyển từ trái sang phải giống như các thuật toán khớp thông thường, nhưng trong quá trình so sánh, ta so sánh từ phải sang trái, tức là dựa trên hậu tố để so sánh.

Dưới đây, chúng ta sẽ giải thích hai chiến lược khởi động khác nhau trong thuật toán BM: "Quy tắc ký tự không hợp lệ" và "Quy tắc di chuyển hậu tố tốt".

2. Chiến lược khởi động trong thuật toán Boyer Moore

2.1 Quy tắc ký tự không hợp lệ

Quy tắc ký tự không hợp lệ (The Bad Character Rule): Khi một ký tự trong chuỗi văn bản T không khớp với một ký tự trong chuỗi mẫu p, ta gọi ký tự không khớp trong chuỗi văn bản T là "ký tự không hợp lệ", lúc này chuỗi mẫu p có thể di chuyển nhanh sang phải.

Số vị trí di chuyển theo "quy tắc ký tự không hợp lệ" được chia thành hai trường hợp:

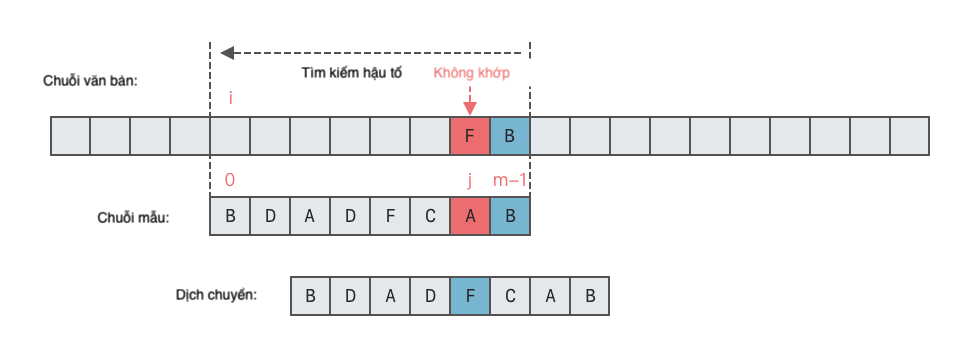
Trường hợp 1: Ký tự không hợp lệ xuất hiện trong chuỗi mẫu p.
- Trong trường hợp này, ta có thể căn chỉnh ký tự không hợp lệ cuối cùng trong chuỗi mẫu với ký tự không hợp lệ trong chuỗi văn bản, như hình dưới đây.
- Số vị trí di chuyển sang phải = Vị trí không khớp của ký tự trong chuỗi mẫu - Vị trí xuất hiện cuối cùng của ký tự không hợp lệ trong chuỗi mẫu.

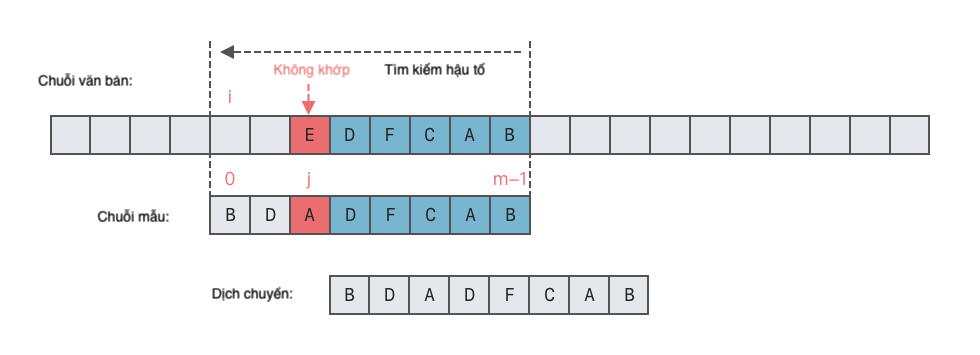
Trường hợp 2: Ký tự không hợp lệ không xuất hiện trong chuỗi mẫu p.
- Trong trường hợp này, ta có thể di chuyển chuỗi mẫu sang phải một vị trí, như hình dưới đây.
- Số vị trí di chuyển sang phải = Vị trí không khớp của ký tự trong chuỗi mẫu + 1.

2.2 Quy tắc hậu tố tốt

Quy tắc di chuyển hậu tố tốt (The Good Suffix Shift Rule): Khi một ký tự trong chuỗi văn bản T không khớp với một ký tự trong chuỗi mẫu p, ta gọi chuỗi con đã khớp trong chuỗi văn bản T là "hậu tố tốt", lúc này chuỗi mẫu p có thể di chuyển nhanh sang phải.

Cách di chuyển theo "quy tắc di chuyển hậu tố tốt" được chia thành ba trường hợp:

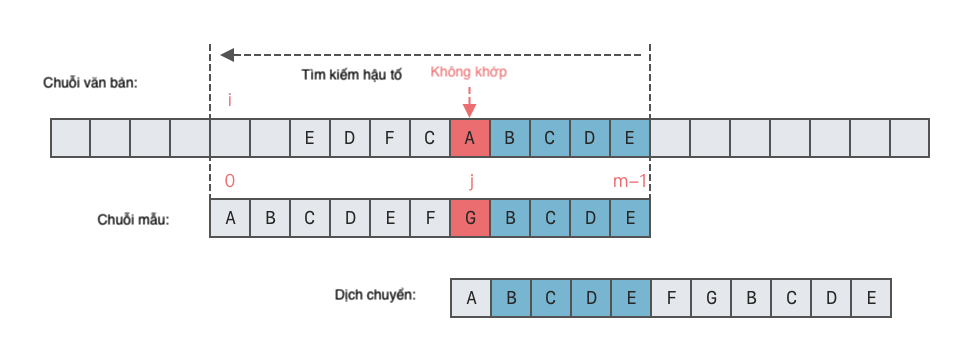
Trường hợp 1: Chuỗi con trong chuỗi mẫu khớp với hậu tố tốt.
- Trong trường hợp này, ta di chuyển chuỗi mẫu để căn chỉnh chuỗi con khớp với hậu tố tốt. Nếu có nhiều hơn một chuỗi con khớp với hậu tố tốt, ta chọn chuỗi con nằm bên phải nhất để căn chỉnh, như hình dưới đây.
- Số vị trí di chuyển sang phải = Vị trí cuối cùng của ký tự trong hậu tố tốt trong chuỗi mẫu - Vị trí xuất hiện cuối cùng của ký tự cuối cùng trong chuỗi con khớp.

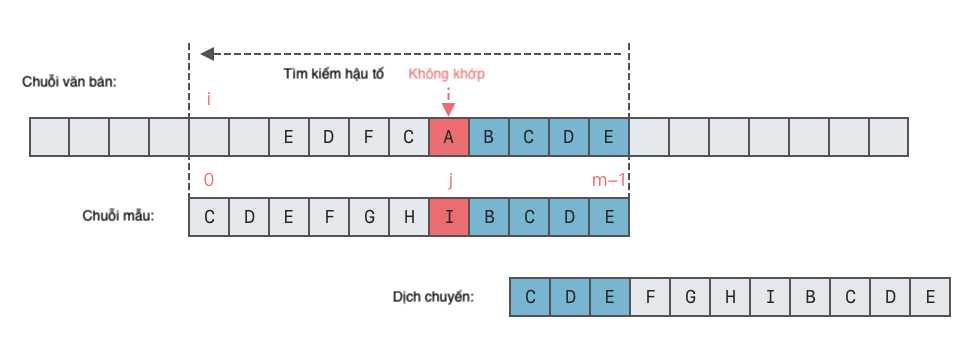
Trường hợp 2: Không có chuỗi con trong chuỗi mẫu khớp với hậu tố tốt, nhưng có tiền tố dài nhất khớp.
- Trong trường hợp này, ta cần tìm một tiền tố dài nhất trong chuỗi mẫu sao cho tiền tố này bằng với hậu tố tốt. Tìm được tiền tố này, ta căn chỉnh tiền tố này với hậu tố tốt.
- Số vị trí di chuyển sang phải = Vị trí cuối cùng của ký tự trong hậu tố tốt trong chuỗi mẫu - Vị trí xuất hiện cuối cùng của ký tự cuối cùng trong tiền tố dài nhất.

Trường hợp 3: Không có chuỗi con trong chuỗi mẫu khớp với hậu tố tốt và không tìm được tiền tố khớp.
- Ta có thể di chuyển toàn bộ chuỗi mẫu sang phải.
- Số vị trí di chuyển sang phải = Độ dài chuỗi mẫu.

3. Ví dụ về quá trình khớp trong thuật toán Boyer Moore

Dưới đây, chúng ta sẽ giới thiệu quá trình khớp trong thuật toán Boyer Moore dựa trên ví dụ được giới thiệu bởi J Strother Moore, đồng thời cũng làm rõ hơn về "Quy tắc ký tự không hợp lệ" và "Quy tắc di chuyển hậu tố tốt".

Giả sử chuỗi văn bản là "HERE IS A SIMPLE EXAMPLE" và chuỗi mẫu là "EXAMPLE", như hình dưới đây.

Đầu tiên, hãy căn chỉnh đầu chuỗi mẫu và đầu chuỗi văn bản, sau đó so sánh từ phần tử cuối cùng của chuỗi mẫu. Như hình dưới đây.

Có thể thấy, ký tự 'S' và 'E' không khớp. Lúc này, ký tự không khớp 'S' được gọi là "ký tự không hợp lệ", tương ứng với vị trí thứ 6 trong chuỗi mẫu. Và 'S' không xuất hiện trong chuỗi mẫu "EXAMPLE" (tương đương với vị trí xuất hiện cuối cùng của 'S' trong chuỗi mẫu là -1). Dựa trên quy tắc ký tự không hợp lệ, ta có thể di chuyển chuỗi mẫu sang phải 6 - (-1) = 7 vị trí, tức là đặt chuỗi mẫu sau ký tự 'S' trong chuỗi văn bản.

Di chuyển chuỗi mẫu sang phải 7 vị trí. Tiếp tục so sánh từ phần tử cuối cùng của chuỗi mẫu, như hình dưới đây.

Tuy nhiên, ký tự 'P' và 'E' không khớp. Ký tự 'P' cũng là ký tự không hợp lệ, như hình dưới đây.

Tuy nhiên, ký tự 'P' xuất hiện trong chuỗi mẫu "EXAMPLE", vị trí không khớp của ký tự 'P' trong chuỗi mẫu là vị trí thứ 6, và vị trí xuất hiện cuối cùng của ký tự cuối cùng trong chuỗi con khớp là 4 (đánh số từ 0). Dựa trên quy tắc ký tự không hợp lệ, ta có thể di chuyển chuỗi mẫu sang phải 6 - 4 = 2 vị trí, đặt chuỗi mẫu sau ký tự 'P' trong chuỗi văn bản.

Di chuyển chuỗi mẫu sang phải 2 vị trí. Tiếp tục so sánh từ phần tử cuối cùng của chuỗi mẫu, như hình dưới đây.

Tiếp tục so sánh phần tử trước đó, tức là ký tự 'L' trong chuỗi văn bản và ký tự 'L' trong chuỗi mẫu, như hình dưới đây. Có thể thấy ký tự 'L' trong chuỗi văn bản và ký tự 'L' trong chuỗi mẫu khớp. Chuỗi "LE" là "hậu tố tốt", vị trí của chuỗi "LE" trong chuỗi mẫu là 6 (đánh số từ 0).

Tiếp tục so sánh phần tử trước đó, tức là ký tự 'P' trong chuỗi văn bản và ký tự 'P' trong chuỗi mẫu, như hình dưới đây. Có thể thấy ký tự 'P' trong chuỗi văn bản và ký tự 'P' trong chuỗi mẫu khớp. Chuỗi "PLE" là "hậu tố tốt", vị trí của chuỗi "PLE" trong chuỗi mẫu là 6 (đánh số từ 0).

Tiếp tục so sánh phần tử trước đó, tức là ký tự 'M' trong chuỗi văn bản và ký tự 'M' trong chuỗi mẫu, như hình dưới đây. Có thể thấy ký tự 'M' trong chuỗi văn bản và ký tự 'M' trong chuỗi mẫu khớp. Chuỗi "MPLE" là "hậu tố tốt", vị trí của chuỗi "MPLE" trong chuỗi mẫu là 6 (đánh số từ 0).

Tiếp tục so sánh phần tử trước đó, tức là ký tự 'I' trong chuỗi văn bản và ký tự 'A' trong chuỗi mẫu, như hình dưới đây. Có thể thấy ký tự 'I' trong chuỗi văn bản và ký tự 'A' trong chuỗi mẫu không khớp.

Lúc này, nếu tuân theo quy tắc ký tự không hợp lệ, chuỗi mẫu sẽ được di chuyển sang phải 2 - (-1) = 3 vị trí. Tuy nhiên, dựa trên quy tắc di chuyển hậu tố tốt, chúng ta có cách di chuyển tốt hơn.

Trong các hậu tố tốt "MPLE", "PLE", "LE", "E", chỉ có hậu tố tốt "E" khớp với tiền tố "E" trong chuỗi mẫu, tương ứng với quy tắc tốt thứ hai. Vị trí cuối cùng của ký tự "E" trong chuỗi mẫu là 6, vị trí cuối cùng của ký tự cuối cùng trong tiền tố dài nhất là 0, dựa trên quy tắc di chuyển hậu tố tốt, ta có thể di chuyển chuỗi mẫu sang phải 6 - 0 = 6 vị trí. Như hình dưới đây.

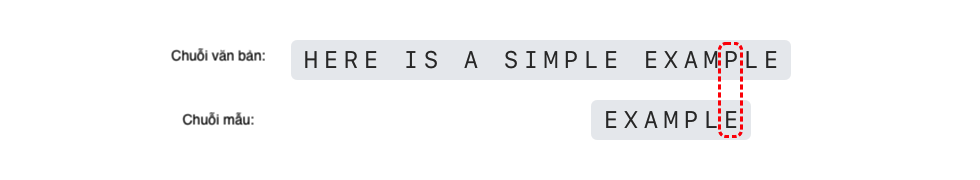
Tiếp tục so sánh từ phần tử cuối cùng của chuỗi mẫu, như hình dưới đây.

Có thể thấy, ký tự 'P' và 'E' không khớp, ký tự 'P' là ký tự không hợp lệ. Dựa trên quy tắc ký tự không hợp lệ, chuỗi mẫu sẽ được di chuyển sang phải 2 - 4 = -2 vị trí, như hình dưới đây.

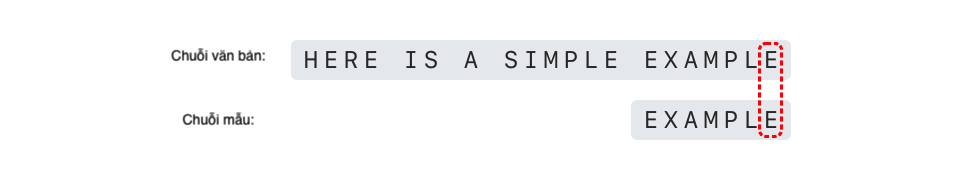
Tiếp tục so sánh từ phần tử cuối cùng của chuỗi mẫu, như hình dưới đây.

Có thể thấy, chuỗi mẫu khớp hoàn toàn, vì vậy quá trình tìm kiếm kết thúc và trả về vị trí của chuỗi mẫu trong chuỗi văn bản.

4. Các bước trong thuật toán Boyer Moore

Các bước của thuật toán Boyer Moore được mô tả như sau:

Tính độ dài của chuỗi văn bản T là n và độ dài của chuỗi mẫu p là m.
Tiền xử lý chuỗi mẫu p bằng cách tạo bảng vị trí ký tự không hợp lệ bc_table và bảng số vị trí di chuyển theo quy tắc di chuyển hậu tố tốt gs_table.
Căn chỉnh phần đầu của chuỗi mẫu p với chuỗi văn bản T, đặt i trỏ đến vị trí bắt đầu của chuỗi văn bản, tức là i = 0. Đặt j trỏ đến vị trí cuối của chuỗi mẫu, tức là j = m - 1, sau đó bắt đầu so sánh từ vị trí cuối của chuỗi mẫu.
1. Nếu ký tự tại vị trí T[i + j] trong chuỗi văn bản khớp với ký tự p[j] trong chuỗi mẫu, tiếp tục so sánh ký tự trước đó.
  1. Nếu đã khớp hết toàn bộ chuỗi mẫu, trả về vị trí bắt đầu của chuỗi mẫu p trong chuỗi văn bản T.
2. Nếu ký tự tại vị trí T[i + j] trong chuỗi văn bản không khớp với ký tự p[j] trong chuỗi mẫu, thực hiện các bước sau:
  1. Tính toán số vị trí di chuyển theo quy tắc ký tự không hợp lệ bad_move dựa trên bảng vị trí ký tự không hợp lệ.
  2. Tính toán số vị trí di chuyển theo quy tắc di chuyển hậu tố tốt good_move dựa trên bảng số vị trí di chuyển theo quy tắc di chuyển hậu tố tốt.
  3. Chọn giá trị lớn nhất giữa hai số vị trí di chuyển này, sau đó di chuyển chuỗi mẫu, tức là i += max(bad_move, good_move).
Nếu di chuyển đến cuối cùng mà không tìm thấy khớp, trả về -1.

5. Cài đặt thuật toán Boyer Moore

Việc cài đặt quá trình khớp của thuật toán BM không quá khó, nhưng khó khăn chính trong việc cài đặt toàn bộ thuật toán đó là giai đoạn tiền xử lý, bao gồm "tạo bảng vị trí ký tự không hợp lệ" và "tạo bảng số vị trí di chuyển theo quy tắc di chuyển hậu tố tốt". Đặc biệt là giai đoạn "tạo bảng số vị trí di chuyển theo quy tắc di chuyển hậu tố tốt", nó rất phức tạp. Dưới đây, chúng ta sẽ trình bày từng bước một.

5.1 Tạo bảng vị trí ký tự không hợp lệ

Cài đặt mã để tạo bảng vị trí ký tự không hợp lệ khá đơn giản. Các bước cụ thể như sau:

Sử dụng một bảng băm bc_table, bc_table[bad_char] đại diện cho vị trí cuối cùng mà ký tự không hợp lệ bad_char xuất hiện trong chuỗi mẫu.
Duyệt qua chuỗi mẫu và lưu trữ ký tự hiện tại p[i] làm khóa và vị trí hiện tại là giá trị trong bảng băm. Nếu có ký tự trùng lặp, giá trị vị trí hiện tại sẽ ghi đè lên giá trị trước đó. Điều này đảm bảo bảng băm chứa vị trí cuối cùng mà ký tự xuất hiện trong chuỗi mẫu.

Điều này có nghĩa là nếu trong quá trình khớp của thuật toán BM, nếu bad_char không có trong bc_table, ta có thể đặt vị trí cuối cùng mà bad_char xuất hiện trong chuỗi mẫu là -1. Nếu bad_char có trong bc_table, vị trí cuối cùng mà bad_char xuất hiện trong chuỗi mẫu sẽ là bc_table[bad_char]. Điều này cho phép tính toán số vị trí có thể di chuyển sang phải.

Mã để tạo bảng vị trí ký tự không hợp lệ như sau:

# Tạo bảng vị trí ký tự không hợp lệ
# bc_table[bad_char] đại diện cho vị trí cuối cùng mà ký tự không hợp lệ xuất hiện trong chuỗi mẫu
def generateBadCharTable(p: str):
    bc_table = dict()
    
    for i in range(len(p)):
        bc_table[p[i]] = i                          # Cập nhật vị trí cuối cùng mà ký tự không hợp lệ xuất hiện trong chuỗi mẫu
    return bc_table

5.2 Tạo bảng dịch chuyển sau khi tạo quy tắc hậu tố tốt

Để tạo bảng di chuyển theo quy tắc hậu tố tốt, chúng ta cần định nghĩa một mảng hậu tố suffix, trong đó suffix[i] = s cho biết độ dài tối đa của một hậu tố của chuỗi con kết thúc tại chỉ số i mà khớp với hậu tố của mẫu. Nghĩa là thỏa mãn p[i-s…i] == p[m-1-s, m-1] với độ dài tối đa là s.

Mã để tạo mảng suffix như sau:

# Tạo mảng hậu tố
# suffix[i] biểu thị độ dài tối đa của một hậu tố của chuỗi con kết thúc tại chỉ số i
def generageSuffixArray(p: str):
    m = len(p)
    suffix = [m for _ in range(m)]                  # Khởi tạo giả định độ dài tối đa là m
    for i in range(m - 2, -1, -1):                  # Hậu tố con bắt đầu từ m - 2
        start = i                                   # start là vị trí bắt đầu của chuỗi con
        while start >= 0 and p[start] == p[m - 1 - i + start]:
            start -= 1                              # Tiến hành so khớp hậu tố, start là vị trí bắt đầu của chuỗi con khớp
        suffix[i] = i - start                       # Cập nhật độ dài tối đa của một hậu tố của chuỗi con kết thúc tại chỉ số i
    return suffix

Có mảng suffix, chúng ta có thể định nghĩa bảng di chuyển theo quy tắc hậu tố tốt gs_list. Chúng ta sử dụng một mảng để biểu thị bảng di chuyển theo quy tắc hậu tố tốt. Trong đó, gs_list[j] biểu thị số vị trí để di chuyển mẫu khi gặp một ký tự sai tại chỉ số j dựa trên quy tắc hậu tố tốt.

Dựa trên quy tắc hậu tố tốt được mô tả trong phần 2.2 Quy tắc hậu tố tốt, chúng ta biết rằng cách di chuyển theo quy tắc hậu tố tốt có thể chia thành ba trường hợp.

Trường hợp 1: Mẫu có một chuỗi con khớp với hậu tố tốt.
Trường hợp 2: Mẫu không có chuỗi con khớp với hậu tố tốt, nhưng có một hậu tố tốt có tiền tố dài nhất khớp.
Trường hợp 3: Mẫu không có chuỗi con khớp với hậu tố tốt và không tìm thấy tiền tố khớp.

Ba trường hợp này có thể được kết hợp lại thành hai trường hợp, vì trường hợp 3 có thể coi là một tiền tố khớp với độ dài 0. Nếu gặp một ký tự sai đồng thời thỏa mãn nhiều trường hợp, chúng ta nên chọn khoảng cách di chuyển nhỏ nhất trong các trường hợp để không bỏ sót các trường hợp khớp có thể.

Để có được giá trị chính xác của gs_list[j], chúng ta có thể giả định tất cả các trường hợp đều là trường hợp 3 ban đầu, tức là gs_list[i] = m.
Sau đó, chúng ta cập nhật giá trị của gs_list tại vị trí ký tự sai trước hậu tố tốt dựa trên phương pháp khớp tiền tố và hậu tố, tức là gs_list[j] = m - 1 - i, trong đó j là vị trí ký tự sai trước hậu tố tốt, i là vị trí cuối cùng của tiền tố dài nhất, m - 1 - i là khoảng cách có thể di chuyển sang phải.
Cuối cùng, chúng ta tính toán giá trị của gs_list tại vị trí ký tự sai trong trường hợp 1, cập nhật số vị trí có thể di chuyển sang phải khi gặp ký tự sai tại điểm bắt đầu của hậu tố tốt (m - 1 - suffix[i]), tức là gs_list[m - 1 - suffix[i]] = m - 1 - i.

Mã để tạo bảng di chuyển theo quy tắc hậu tố tốt gs_list như sau:

# Tạo bảng di chuyển theo quy tắc hậu tố tốt
# gs_list[j] biểu thị số vị trí để di chuyển mẫu khi gặp ký tự sai tại chỉ số j dựa trên quy tắc hậu tố tốt
def generageGoodSuffixList(p: str):
    # Bảng di chuyển theo quy tắc hậu tố tốt
    # Trường hợp 1: Mẫu có một chuỗi con khớp với hậu tố tốt
    # Trường hợp 2: Mẫu không có chuỗi con khớp với hậu tố tốt, nhưng có một hậu tố tốt có tiền tố dài nhất khớp
    # Trường hợp 3: Mẫu không có chuỗi con khớp với hậu tố tốt và không tìm thấy tiền tố khớp
    
    m = len(p)
    gs_list = [m for _ in range(m)]                 # Trường hợp 3: Khởi tạo giả định là trường hợp 3 cho tất cả các vị trí
    suffix = generageSuffixArray(p)                 # Tạo mảng hậu tố
    
    j = 0                                           # j là vị trí ký tự sai trước hậu tố tốt
    for i in range(m - 1, -1, -1):                  # Trường hợp 2: Bắt đầu từ tiền tố dài nhất
        if suffix[i] == i + 1:                      # Khớp với tiền tố, tức là p[0...i] == p[m-1-i...m-1]
            while j < m - 1 - i:
                if gs_list[j] == m:
                    gs_list[j] = m - 1 - i          # Cập nhật số vị trí có thể di chuyển sang phải khi gặp ký tự sai
                j += 1
        
    for i in range(m - 1):                          # Trường hợp 1: Khớp với chuỗi con, p[i-s...i] == p[m-1-s, m-1]
        gs_list[m - 1 - suffix[i]] = m - 1 - i      # Cập nhật số vị trí có thể di chuyển sang phải khi gặp ký tự sai tại điểm bắt đầu của hậu tố tốt
    return gs_list

5.3 Triển khai tổng thể của thuật toán Boyer Moore

# Thuật toán Boyer Moore
def boyerMoore(T: str, p: str) -> int:
    n, m = len(T), len(p)
    
    bc_table = generateBadCharTable(p)              # Tạo bảng di chuyển ký tự sai
    gs_list = generageGoodSuffixList(p)             # Tạo bảng di chuyển theo quy tắc hậu tố tốt
    
    i = 0
    while i <= n - m:
        j = m - 1
        while j > -1 and T[i + j] == p[j]:          # Tiến hành so khớp hậu tố, thoát khỏi vòng lặp nếu gặp ký tự sai
            j -= 1
        if j < 0:
            return i                                # Khớp hoàn thành, trả về vị trí xuất hiện của mẫu p trong chuỗi T
        bad_move = j - bc_table.get(T[i + j], -1)   # Số vị trí di chuyển theo quy tắc ký tự sai
        good_move = gs_list[j]                      # Số vị trí di chuyển theo quy tắc hậu tố tốt
        i += max(bad_move, good_move)               # Di chuyển theo số vị trí lớn nhất giữa hai quy tắc
    return -1
            
    
# Tạo bảng di chuyển ký tự sai
# bc_table[bad_char] biểu thị vị trí cuối cùng xuất hiện của ký tự sai trong mẫu
def generateBadCharTable(p: str):
    bc_table = dict()
    
    for i in range(len(p)):
        bc_table[p[i]] = i                          # Cập nhật vị trí cuối cùng xuất hiện của ký tự sai trong mẫu
    return bc_table

# Tạo bảng di chuyển theo quy tắc hậu tố tốt
# gs_list[j] biểu thị số vị trí di chuyển sang phải khi gặp ký tự sai tại chỉ số j dựa trên quy tắc hậu tố tốt
def generageGoodSuffixList(p: str):
    # Bảng di chuyển theo quy tắc hậu tố tốt
    # Trường hợp 1: Mẫu có một chuỗi con khớp với hậu tố tốt
    # Trường hợp 2: Mẫu không có chuỗi con khớp với hậu tố tốt, nhưng có một hậu tố tốt có tiền tố dài nhất khớp
    # Trường hợp 3: Mẫu không có chuỗi con khớp với hậu tố tốt và không tìm thấy tiền tố khớp
    
    m = len(p)
    gs_list = [m for _ in range(m)]                 # Trường hợp 3: Khởi tạo giả định là trường hợp 3 cho tất cả các vị trí
    suffix = generageSuffixArray(p)                 # Tạo mảng hậu tố
    
    j = 0                                           # j là vị trí ký tự sai trước hậu tố tốt
    for i in range(m - 1, -1, -1):                  # Trường hợp 2: Bắt đầu từ tiền tố dài nhất
        if suffix[i] == i + 1:                      # Khớp với tiền tố, tức là p[0...i] == p[m-1-i...m-1]
            while j < m - 1 - i:
                if gs_list[j] == m:
                    gs_list[j] = m - 1 - i          # Cập nhật số vị trí di chuyển sang phải khi gặp ký tự sai
                j += 1
        
    for i in range(m - 1):                          # Trường hợp 1: Khớp với chuỗi con, p[i-s...i] == p[m-1-s, m-1]
        gs_list[m - 1 - suffix[i]] = m - 1 - i      # Cập nhật số vị trí di chuyển sang phải khi gặp ký tự sai tại điểm bắt đầu của hậu tố tốt
    return gs_list

# Tạo mảng hậu tố
# suffix[i] biểu thị độ dài tối đa của một hậu tố của chuỗi con kết thúc tại chỉ số i
def generageSuffixArray(p: str):
    m = len(p)
    suffix = [m for _ in range(m)]                  # Khởi tạo giả định độ dài tối đa là m
    for i in range(m - 2, -1, -1):                  # Hậu tố con bắt đầu từ m - 2
        start = i                                   # start là vị trí bắt đầu của chuỗi con
        while start >= 0 and p[start] == p[m - 1 - i + start]:
            start -= 1                              # Tiến hành so khớp hậu tố, start là vị trí bắt đầu của chuỗi con khớp
        suffix[i] = i - start                       # Cập nhật độ dài tối đa của một hậu tố của chuỗi con kết thúc tại chỉ số i
    return suffix

print(boyerMoore("abbcfdddbddcaddebc", "aaaaa"))
print(boyerMoore("", ""))

6. Phân tích thuật toán Boyer Moore

Thuật toán Boyer Moore có độ phức tạp thời gian trong giai đoạn tiền xử lý là $O(n + \sigma)$ , trong đó $\sigma$ là kích thước của bảng ký tự.
Trong giai đoạn tìm kiếm, trường hợp tốt nhất của thuật toán Boyer Moore là khi mỗi lần so khớp, không có ký tự nào trong mẫu p khớp với ký tự đầu tiên trong chuỗi văn bản T. Trong trường hợp này, độ phức tạp thời gian là $O(n / m)$ .
Trong giai đoạn tìm kiếm, trường hợp xấu nhất của thuật toán Boyer Moore là khi chuỗi văn bản T có nhiều ký tự trùng lặp và mẫu p có m - 1 ký tự giống nhau trước khi thêm một ký tự khác. Trong trường hợp này, độ phức tạp thời gian là $O(m * n)$ .
Khi mẫu p không có chu kỳ, trong trường hợp xấu nhất, thuật toán Boyer Moore cần tối đa $3 * n$ lần so sánh ký tự.