Horspool

1.1 Giới thiệu thuật toán Horspool

Thuật toán Horspool: là một thuật toán tìm kiếm chuỗi con trong chuỗi, được phát triển bởi giáo sư Nigel Horspool vào năm 1980, là phiên bản đơn giản hóa đầu tiên của thuật toán Boyer Moore.

Ý tưởng của thuật toán Horspool: Đối với chuỗi văn bản T và chuỗi mẫu p đã cho, trước tiên ta xử lý chuỗi mẫu p. Sau đó trong quá trình so khớp, khi ta phát hiện một ký tự trong chuỗi văn bản T không khớp với chuỗi mẫu p, dựa trên chiến lược thông minh, ta có thể bỏ qua một số trường hợp không khớp và di chuyển chuỗi mẫu sang phải càng nhiều vị trí càng tốt.

Có thể thấy, ý tưởng của thuật toán Horspool tương tự như thuật toán Boyer Moore. Thuật toán Horspool là một phiên bản đơn giản hóa của thuật toán Boyer Moore, tập trung vào việc cải tiến "quy tắc ký tự sai". Khi ta gặp một ký tự không khớp giữa chuỗi văn bản T và chuỗi mẫu p, ta có thể di chuyển chuỗi mẫu p nhanh chóng sang phải.

Khi gặp ký tự không khớp, ta có thể di chuyển nhanh sang phải dựa trên hai trường hợp sau:

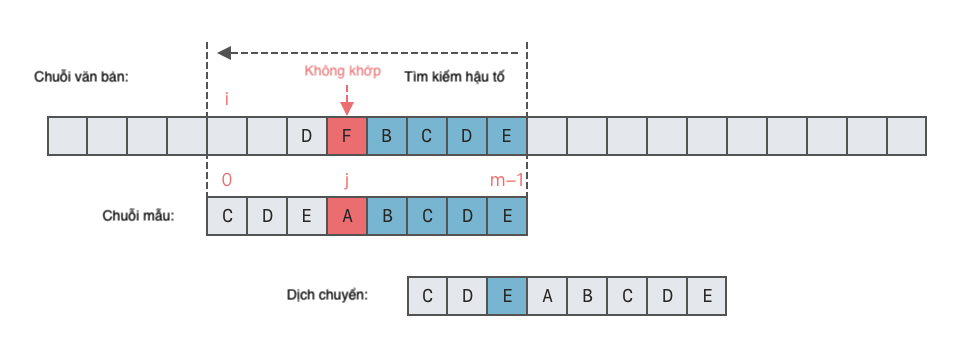
Trường hợp 1: Ký tự T[i + m - 1] trong chuỗi văn bản T tương ứng với ký tự cuối cùng p[m - 1] trong chuỗi mẫu p xuất hiện trong chuỗi mẫu p.
- Trong trường hợp này, ta có thể căn chỉnh T[i + m - 1] với vị trí cuối cùng xuất hiện của ký tự đó trong chuỗi mẫu p, như hình minh họa dưới đây.
- Số vị trí di chuyển sang phải = Vị trí cuối cùng của ký tự cuối cùng trong chuỗi mẫu - Vị trí cuối cùng xuất hiện của ký tự T[i + m - 1] trong chuỗi mẫu p.
- Lưu ý: Vị trí cuối cùng của ký tự cuối cùng trong chuỗi mẫu chính là "độ dài chuỗi mẫu - 1".

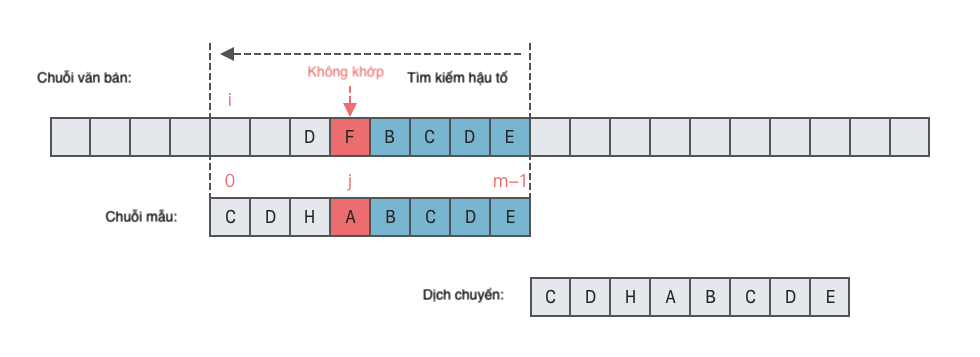
Trường hợp 2: Ký tự T[i + m - 1] trong chuỗi văn bản T tương ứng với ký tự cuối cùng p[m - 1] trong chuỗi mẫu p không xuất hiện trong chuỗi mẫu p.
- Trong trường hợp này, ta có thể di chuyển toàn bộ chuỗi mẫu sang phải, như hình minh họa dưới đây.
- Số vị trí di chuyển sang phải = Độ dài toàn bộ chuỗi mẫu.

2. Các bước của thuật toán Horspool

Các bước của thuật toán Horspool được mô tả như sau:

Tính độ dài của chuỗi văn bản T là n và độ dài của chuỗi mẫu p là m.
Tiến hành xử lý trước cho chuỗi mẫu p, tạo bảng di chuyển bc_table.
Căn chỉnh phần đầu của chuỗi mẫu p với chuỗi văn bản T, đặt i trỏ đến vị trí bắt đầu của chuỗi văn bản, tức là i = 0. j trỏ đến vị trí cuối cùng của chuỗi mẫu, tức là j = m - 1, sau đó bắt đầu so sánh từ vị trí cuối cùng của chuỗi mẫu.
1. Nếu ký tự T[i + j] trong chuỗi văn bản khớp với ký tự p[j] trong chuỗi mẫu, tiếp tục so sánh ký tự trước đó.
  1. Nếu toàn bộ chuỗi mẫu khớp, trả về vị trí bắt đầu của chuỗi mẫu p trong chuỗi văn bản T.
2. Nếu ký tự T[i + j] trong chuỗi văn bản không khớp với ký tự p[j] trong chuỗi mẫu, ta thực hiện:
  1. Dựa trên bảng di chuyển bc_table và ký tự tương ứng với vị trí cuối cùng của chuỗi mẫu trong chuỗi văn bản T[i + m - 1], tính toán số vị trí có thể di chuyển bc_table[T[i + m - 1]], sau đó di chuyển chuỗi mẫu sang phải.
Nếu di chuyển đến cuối mà không tìm thấy trường hợp khớp, trả về -1.

3. Triển khai thuật toán Horspool

3.1 Tạo bảng số dịch chuyển

Việc tạo bảng số dịch chuyển sau làm việc khá đơn giản, tương tự như việc tạo bảng vị trí ký tự xấu trong thuật toán Boyer Moore. Các bước cụ thể như sau:

Sử dụng một bảng băm bc_table, bc_table[bad_char] đại diện cho khoảng cách có thể dịch chuyển sang phải khi gặp ký tự xấu.
Duyệt qua chuỗi mẫu, với ký tự hiện tại p[i] làm khóa, khoảng cách có thể dịch chuyển sang phải (m - 1 - i) làm giá trị và lưu vào từ điển. Nếu có ký tự trùng lặp, giá trị vị trí mới sẽ ghi đè lên giá trị trước đó. Như vậy, bảng băm sẽ lưu trữ khoảng cách có thể dịch chuyển sang phải từ vị trí xuất hiện cuối cùng của ký tự đó trong chuỗi mẫu.

Trong quá trình khớp của thuật toán Horspool, nếu T[i + m - 1] không có trong bc_table, ta có thể đặt giá trị của nó là m, đại diện cho việc có thể dịch chuyển toàn bộ chuỗi mẫu sang phải. Nếu T[i + m - 1] có trong bc_table, khoảng cách có thể dịch chuyển là bc_table[T[i + m - 1]]. Như vậy, ta có thể tính được số lượng bit có thể dịch chuyển sang phải.

Đoạn mã tạo bảng số dịch chuyển như sau:

# tạo bảng di chuyển với ký tự sai
# bc_table[ký tự sai] đại diện cho khoảng cách di chuyển sang phải khi gặp ký tự sai
def generateBadCharTable(p: str):
    m = len(p)
    bc_table = dict()
    
    for i in range(m - 1):                      # lặp cho đến m - 2
        bc_table[p[i]] = m - 1 - i              # cập nhật khoảng cách di chuyển sang phải khi gặp ký tự sai
    return bc_table

3.2 Triển khai tổng thể của thuật toán Horspool

# thuật toán horspool, T là chuỗi văn bản, p là chuỗi mẫu
def horspool(T: str, p: str) -> int:
    n, m = len(T), len(p)
    
    bc_table = generateBadCharTable(p)          # tạo bảng di chuyển với ký tự sai
    
    i = 0
    while i <= n - m:
        j = m - 1
        while j > -1 and T[i + j] == p[j]:      # thực hiện so khớp hậu tố, thoát khỏi vòng lặp nếu gặp ký tự sai
            j -= 1
        if j < 0:
            return i                            # khớp hoàn tất, trả về vị trí của chuỗi mẫu p trong chuỗi văn bản T
        i += bc_table.get(T[i + m - 1], m)      # di chuyển sang phải sử dụng bảng di chuyển với ký tự sai
    return -1                                   # không khớp

# tạo bảng di chuyển với ký tự sai
# bc_table[ký tự sai] đại diện cho khoảng cách di chuyển sang phải khi gặp ký tự sai
def generateBadCharTable(p: str):
    m = len(p)
    bc_table = dict()
    
    for i in range(m - 1):                      # lặp cho đến m - 2
        bc_table[p[i]] = m - 1 - i              # cập nhật khoảng cách di chuyển sang phải khi gặp ký tự sai
    return bc_table

print(horspool("abbcfdddbddcaddebc", "aaaaa"))
print(horspool("abbcfdddbddcaddebc", "bcf"))

4. Phân tích thuật toán Horspool

Thuật toán Horspool có độ phức tạp thời gian trung bình là $O(n)$ , nhưng trong trường hợp xấu nhất, độ phức tạp thời gian có thể lên đến $O(n * m)$ .