Skip to main content

Binary Tree Traversal

Hung NguyenAbout 11 mindsaalgorithmdsaalgorithm

1. Giới thiệu về duyệt cây nhị phân

Duyệt cây nhị phân: Được hiểu là từ nút gốc, theo một thứ tự nào đó, truy cập lần lượt vào tất cả các nút trong cây nhị phân, sao cho mỗi nút chỉ được truy cập một lần và chỉ một lần.

Trong một số bài toán thực tế liên quan đến cây nhị phân, chúng ta thường cần truy cập từng nút trong cây nhị phân theo một thứ tự nhất định, để tìm kiếm các nút có một đặc điểm cụ thể hoặc tất cả các nút, sau đó xử lý các nút này. Ở đây, "truy cập" có nghĩa là thực hiện một thao tác nào đó trên nút đó, ví dụ: xuất thông tin dữ liệu của nút, đếm số lượng nút thỏa mãn một điều kiện nào đó, v.v.

Xem lại định nghĩa đệ quy của cây nhị phân, ta biết rằng cây nhị phân được tạo thành từ nút gốc và cây con trái, cây con phải. Do đó, nếu chúng ta có thể duyệt lần lượt ba phần này, ta có thể duyệt toàn bộ cây nhị phân.

Nếu sử dụng phương pháp tìm kiếm theo chiều sâu và tuân theo một thứ tự truy cập khác nhau, chúng ta có thể chia thành 6 phương pháp duyệt khác nhau. Nếu giới hạn thứ tự truy cập là trước cây con trái sau đó cây con phải, ta có tổng cộng 3 phương pháp duyệt: duyệt cây nhị phân theo thứ tự trước, duyệt cây nhị phân theo thứ tự giữa và duyệt cây nhị phân theo thứ tự sau.

Nếu sử dụng phương pháp tìm kiếm theo chiều rộng, ta có thể duyệt cây nhị phân theo thứ tự từ trên xuống dưới theo từng tầng (từ trái qua phải), phương pháp này được gọi là duyệt cây nhị phân theo tầng.

2. Duyệt cây nhị phân theo thứ tự trước

Quy tắc duyệt cây nhị phân theo thứ tự trước như sau:

  • Nếu cây nhị phân rỗng, trả về.
  • Nếu cây nhị phân không rỗng, thực hiện các bước sau:
    1. Truy cập vào nút gốc.
    2. Duyệt cây con trái của nút gốc theo thứ tự trước.
    3. Duyệt cây con phải của nút gốc theo thứ tự trước.

Từ quy tắc duyệt cây nhị phân theo thứ tự trước, ta có thể thấy quá trình duyệt là một quá trình đệ quy. Khi duyệt bất kỳ cây con nào, ta vẫn tuân thủ quy tắc trước tiên truy cập vào nút gốc, sau đó duyệt cây con trái của nút gốc, cuối cùng là duyệt cây con phải của nút gốc.

Như hình dưới đây, thứ tự duyệt cây nhị phân này là: A - B - D - H - I - E - C - F - J - G - K.

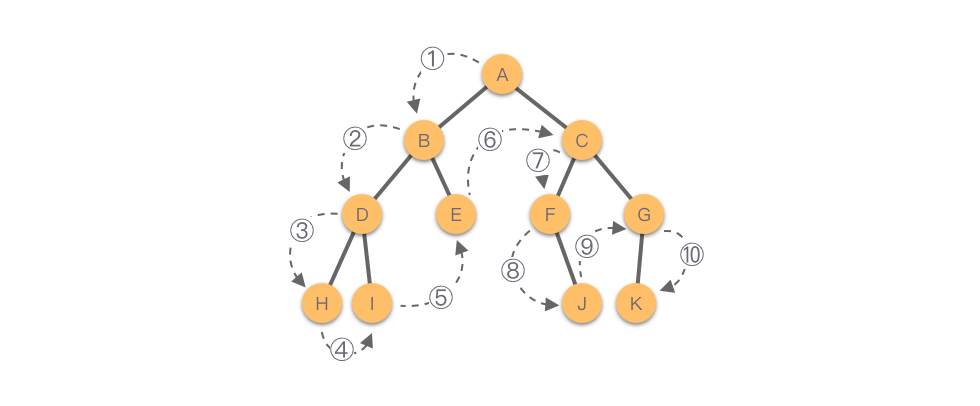
20220222165249.png
20220222165249.png

2.1 Duyệt cây nhị phân theo thứ tự trước bằng đệ quy

Các bước thực hiện duyệt cây nhị phân theo thứ tự trước bằng đệ quy như sau:

  1. Kiểm tra xem cây nhị phân có rỗng không, nếu rỗng thì trả về.
  2. Truy cập vào nút gốc.
  3. Đệ quy duyệt cây con trái.
  4. Đệ quy duyệt cây con phải.

Đoạn code dưới đây thực hiện duyệt cây nhị phân theo thứ tự trước bằng đệ quy:

class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        res = []
        
        def preorder(root):
            if not root:
                return
            res.append(root.val)
            preorder(root.left)
            preorder(root.right)

        preorder(root)
        return res

2.2 Duyệt cây nhị phân theo thứ tự trước bằng ngăn xếp

Quá trình duyệt cây nhị phân theo thứ tự trước bằng đệ quy thực chất là quá trình sử dụng ngăn xếp của hệ thống. Chúng ta cũng có thể sử dụng một ngăn xếp stack để mô phỏng quá trình đệ quy.

Thứ tự duyệt cây nhị phân theo thứ tự trước là: gốc - cây con trái - cây con phải. Và theo tính chất "LIFO" của ngăn xếp, ta cần đưa cây con phải vào ngăn xếp trước, sau đó đưa cây con trái vào ngăn xếp. Điều này đảm bảo thứ tự duyệt cuối cùng sẽ là thứ tự duyệt cây nhị phân theo thứ tự trước.

Các bước để duyệt cây nhị phân theo thứ tự trước bằng ngăn xếp như sau:

  1. Kiểm tra xem cây nhị phân có rỗng không, nếu rỗng thì trả về.
  2. Khởi tạo một ngăn xếp stack và đưa nút gốc vào ngăn xếp.
  3. Khi ngăn xếp không rỗng:
    1. Lấy phần tử trên đỉnh của ngăn xếp là node và thêm giá trị của node vào kết quả.
    2. Nếu cây con phải của node không rỗng, đưa cây con phải vào ngăn xếp.
    3. Nếu cây con trái của node không rỗng, đưa cây con trái vào ngăn xếp.

Đoạn code dưới đây thực hiện duyệt cây nhị phân theo thứ tự trước bằng ngăn xếp :

class Solution:
    def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        if not root:                        # Kiểm tra cây nhị phân có rỗng không
            return []
            
        res = []
        stack = [root]                      # Khởi tạo ngăn xếp và đưa nút gốc vào ngăn xếp

        while stack:                        # Khi ngăn xếp không rỗng
            node = stack.pop()              # Lấy phần tử trên đỉnh ngăn xếp
            res.append(node.val)            # Thêm giá trị của nút vào kết quả
            if node.right:
                stack.append(node.right)    # Đưa cây con phải vào ngăn xếp
            if node.left:
                stack.append(node.left)     # Đưa cây con trái vào ngăn xếp

        return res

3. Duyệt cây nhị phân theo thứ tự giữa

Quy tắc duyệt cây nhị phân theo thứ tự giữa như sau:

  • Nếu cây nhị phân rỗng, trả về.
  • Nếu cây nhị phân không rỗng, thực hiện các bước sau:
    1. Duyệt cây con trái của nút gốc theo thứ tự giữa.
    2. Truy cập vào nút gốc.
    3. Duyệt cây con phải của nút gốc theo thứ tự giữa.

Từ quy tắc duyệt cây nhị phân theo thứ tự giữa, ta có thể thấy quá trình duyệt là một quá trình đệ quy. Khi duyệt bất kỳ cây con nào, ta vẫn tuân thủ quy tắc trước tiên duyệt cây con trái, sau đó truy cập vào nút gốc, cuối cùng là duyệt cây con phải của nút gốc.

Như hình dưới đây, thứ tự duyệt cây nhị phân này là: H - D - I - B - E - A - F - J - C - K - G.

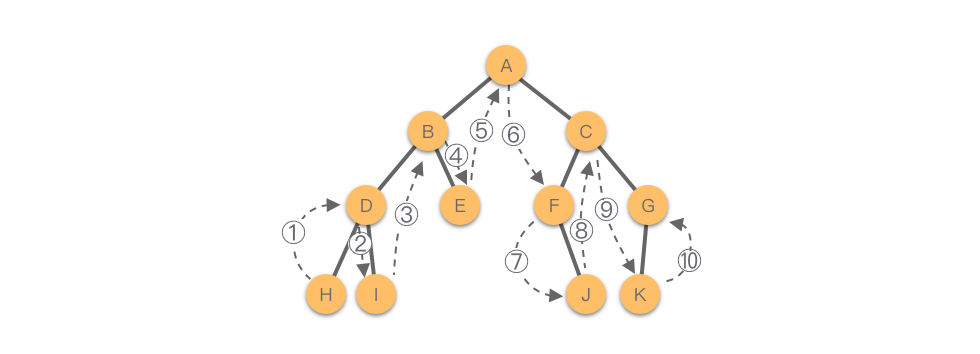
20220222165231.png
20220222165231.png

3.1 Duyệt cây nhị phân theo thứ tự giữa bằng đệ quy

Các bước thực hiện duyệt cây nhị phân theo thứ tự giữa bằng đệ quy như sau:

  1. Kiểm tra xem cây nhị phân có rỗng không, nếu rỗng thì trả về.
  2. Đệ quy duyệt cây con trái.
  3. Truy cập vào nút gốc.
  4. Đệ quy duyệt cây con phải.

Đoạn code dưới đây thực hiện duyệt cây nhị phân theo thứ tự giữa bằng đệ quy:

class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        res = []
        def inorder(root):
            if not root:
                return
            inorder(root.left)
            res.append(root.val)
            inorder(root.right)

        inorder(root)
        return res

3.2 Duyệt cây nhị phân theo thứ tự giữa bằng ngăn xếp

Chúng ta có thể sử dụng một ngăn xếp stack để mô phỏng quá trình duyệt cây nhị phân theo thứ tự giữa bằng đệ quy.

Khác với duyệt cây nhị phân theo thứ tự trước, việc truy cập vào nút gốc phải được thực hiện sau khi duyệt cây con trái. Do đó, chúng ta cần đảm bảo rằng: trước khi duyệt cây con trái, nút hiện tại không được phép bị loại bỏ khỏi ngăn xếp.

Chúng ta bắt đầu từ nút gốc và lặp lại việc duyệt cây con trái, liên tục đưa nút gốc của cây con hiện tại vào ngăn xếp, cho đến khi nút hiện tại không có cây con trái, sau đó lấy nút đó ra khỏi ngăn xếp và xử lý.

Sau đó, chúng ta duyệt cây con phải của nút đó và thực hiện lại quá trình duyệt cây con trái. Điều này đảm bảo thứ tự duyệt cuối cùng sẽ là thứ tự duyệt cây nhị phân theo thứ tự giữa.

Các bước để duyệt cây nhị phân theo thứ tự giữa bằng ngăn xếp như sau:

  1. Kiểm tra xem cây nhị phân có rỗng không, nếu rỗng thì trả về.
  2. Khởi tạo một ngăn xếp stack rỗng.
  3. Khi nút gốc hoặc ngăn xếp không rỗng:
    1. Nếu nút hiện tại không rỗng, lặp lại việc duyệt cây con trái và liên tục đưa nút gốc của cây con hiện tại vào ngăn xếp.
    2. Nếu nút hiện tại rỗng, điều đó có nghĩa là nút hiện tại không có cây con trái, lấy nút đó ra khỏi ngăn xếp và xử lý.
    3. Duyệt cây con phải của nút đó và thực hiện lại quá trình duyệt cây con trái.

Đoạn code dưới đây thực hiện duyệt cây nhị phân theo thứ tự giữa bằng ngăn xếp :

class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        if not root:                # Kiểm tra cây nhị phân có rỗng không
            return []
        
        res = []
        stack = []

        while root or stack:        # Nút gốc hoặc ngăn xếp không rỗng
            while root:             
                stack.append(root)  # Đưa nút gốc của cây con hiện tại vào ngăn xếp
                root = root.left    # Duyệt cây con trái
            
            node = stack.pop()      # Nút hiện tại không có cây con trái, lấy nút đó ra khỏi ngăn xếp
            res.append(node.val)    # Xử lý nút đó
            root = node.right       # Duyệt cây con phải
        return res

4. Duyệt cây nhị phân theo thứ tự sau

Quy tắc duyệt cây nhị phân theo thứ tự sau như sau:

  • Nếu cây nhị phân rỗng, trả về.
  • Nếu cây nhị phân không rỗng, thực hiện các bước sau:
    1. Duyệt cây con trái của nút gốc theo thứ tự sau.
    2. Duyệt cây con phải của nút gốc theo thứ tự sau.
    3. Truy cập vào nút gốc.

Từ quy tắc duyệt cây nhị phân theo thứ tự sau, ta có thể thấy quá trình duyệt là một quá trình đệ quy. Khi duyệt bất kỳ cây con nào, ta vẫn tuân thủ quy tắc trước tiên duyệt cây con trái, sau đó duyệt cây con phải, cuối cùng là truy cập vào nút gốc.

Như hình dưới đây, thứ tự duyệt cây nhị phân này là: H - I - D - E - B - J - F - K - G - C - A.

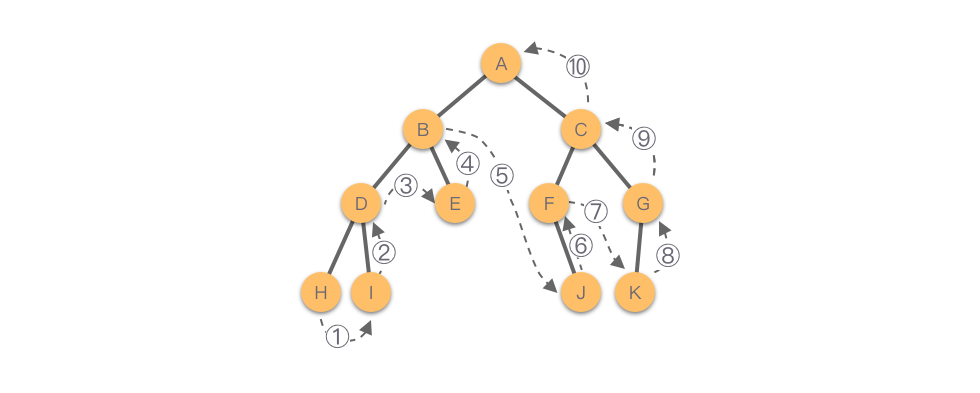
20220222165218.png
20220222165218.png

4.1 Duyệt cây nhị phân theo thứ tự sau bằng đệ quy

Các bước thực hiện duyệt cây nhị phân theo thứ tự sau bằng đệ quy như sau:

  1. Kiểm tra xem cây nhị phân có rỗng không, nếu rỗng thì trả về.
  2. Đệ quy duyệt cây con trái.
  3. Đệ quy duyệt cây con phải.
  4. Truy cập vào nút gốc.

Đoạn code dưới đây thực hiện duyệt cây nhị phân theo thứ tự sau bằng đệ quy:

class Solution:
    def postorderTraversal(self, root: TreeNode) -> List[int]:
        res = []
        def postorder(root):
            if not root:
                return
            postorder(root.left)
            postorder(root.right)
            res.append(root.val)

        postorder(root)
        return res

4.2 Duyệt cây nhị phân theo thứ tự sau bằng ngăn xếp

Chúng ta có thể sử dụng một ngăn xếp  stack để mô phỏng quá trình duyệt cây nhị phân theo thứ tự sau bằng đệ quy.

Khác với duyệt cây nhị phân theo thứ tự trước và giữa, việc truy cập vào nút gốc phải được thực hiện sau khi duyệt cây con trái và cây con phải. Do đó, chúng ta cần đảm bảo rằng: trước khi duyệt cây con trái và cây con phải, nút hiện tại không được phép bị loại bỏ khỏi ngăn xếp.

Chúng ta bắt đầu từ nút gốc và lặp lại việc duyệt cây con trái, sau đó duyệt cây con phải, và cuối cùng là truy cập vào nút gốc. Điều này đảm bảo thứ tự duyệt cuối cùng sẽ là thứ tự duyệt cây nhị phân theo thứ tự sau.

Các bước để duyệt cây nhị phân theo thứ tự sau bằng ngăn xếp như sau:

  1. Kiểm tra xem cây nhị phân có rỗng không, nếu rỗng thì trả về.
  2. Khởi tạo một ngăn xếp stack rỗng.
  3. Khi nút gốc hoặc ngăn xếp không rỗng:
    1. Nếu nút hiện tại không rỗng, lặp lại việc duyệt cây con trái và cây con phải, và đưa nút gốc của cây con hiện tại vào ngăn xếp.
    2. Nếu nút hiện tại rỗng, điều đó có nghĩa là nút hiện tại không có cây con trái và cây con phải, lấy nút đó ra khỏi ngăn xếp và xử lý.

Đoạn code dưới đây thực hiện duyệt cây nhị phân theo thứ tự sau bằng ngăn xếp :

class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        if not root:                # Kiểm tra cây nhị phân có rỗng không
            return []
        
        res = []
        stack = []

        while root or stack:        # Nút gốc hoặc ngăn xếp không rỗng
            while root:
                if root.right:      # Nếu cây con phải không rỗng, đưa nút gốc của cây con phải vào ngăn xếp
                    stack.append(root.right)
                stack.append(root)  # Đưa nút gốc của cây con hiện tại vào ngăn xếp
                root = root.left    # Duyệt cây con trái
            
            node = stack.pop()      # Lấy nút đó ra khỏi ngăn xếp

            # Nếu cây con phải không rỗng và nút gốc của cây con phải chưa được xử lý
            if node.right and stack and stack[-1] == node.right:
                stack.pop()         # Lấy nút gốc của cây con phải ra khỏi ngăn xếp
                stack.append(node)  # Đưa nút gốc của cây con hiện tại vào ngăn xếp
                root = node.right   # Duyệt cây con phải
            else:
                res.append(node.val)# Xử lý nút đó
                
        return res

5. Duyệt cây theo tầng

Quy tắc duyệt cây theo tầng của cây nhị phân là:

  • Nếu cây nhị phân rỗng, trả về.
  • Nếu cây nhị phân không rỗng, thực hiện các bước sau:
    1. Duyệt qua các nút của tầng thứ 1 của cây nhị phân.
    2. Tiếp theo, duyệt qua các nút của tầng thứ 2 của cây nhị phân.
    3. ……
    4. Tiếp tục duyệt qua các tầng tiếp theo, cho đến khi duyệt qua tầng cuối cùng của cây.

Từ quy tắc duyệt cây theo tầng của cây nhị phân, ta có thể thấy quá trình duyệt là một quá trình tìm kiếm theo chiều rộng. Trong quá trình duyệt, ta duyệt qua các tầng 1, 2, …… cuối cùng của cây theo thứ tự từ trái sang phải.

Như hình dưới đây, thứ tự duyệt cây theo tầng của cây nhị phân này là: A - B - C - D - E - F - G - H - I - J - K.

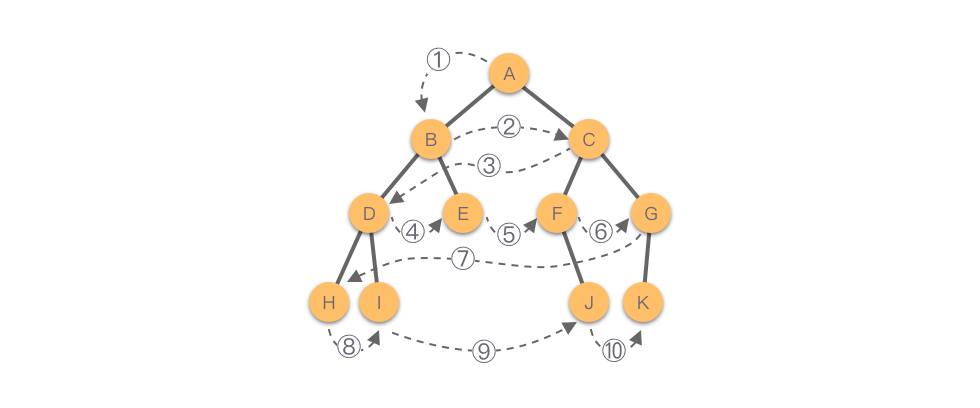
20220222165159.png
20220222165159.png

Duyệt cây theo tầng của cây nhị phân được thực hiện thông qua hàng đợi (queue). Các bước cụ thể như sau:

  1. Kiểm tra cây nhị phân có rỗng không, nếu rỗng thì trả về kết quả rỗng.
  2. Đưa nút gốc vào hàng đợi.
  3. Khi hàng đợi không rỗng, lấy độ dài hiện tại của hàng đợi là .
  4. Lần lượt lấy ra  phần tử từ hàng đợi và duyệt qua từng phần tử này. Sau đó, thêm các nút con trái và phải của phần tử này vào hàng đợi, tiếp tục duyệt qua các nút của tầng tiếp theo.
  5. Khi hàng đợi rỗng, kết thúc quá trình duyệt.

Đoạn mã dưới đây thực hiện duyệt cây theo tầng của cây nhị phân:

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []
        queue = [root]
        order = []
        while queue:
            level = []
            size = len(queue)
            for _ in range(size):
                curr = queue.pop(0)
                level.append(curr.val)
                if curr.left:
                    queue.append(curr.left)
                if curr.right:
                    queue.append(curr.right)
            if level:
                order.append(level)
        return order
Made with ❤️ by Hung Nguyen
Copyright © 2016-2024 Hung Nguyen