Binary Tree Basic
1. Giới thiệu về cây
1.1 Định nghĩa cây
Cây (Tree): Là một tập hợp hữu hạn gồm nút và các mối quan hệ giữa các nút trong tập hợp đó. Khi , cây được gọi là cây rỗng (empty tree), khi , cây được gọi là cây không rỗng (non-empty tree).
Cây được gọi là cây bởi vì cấu trúc dữ liệu này trông giống như một cây đổ ngược, tức là cây trong cấu trúc dữ liệu này có gốc hướng lên trên và các lá hướng xuống dưới. Ví dụ như hình dưới đây:
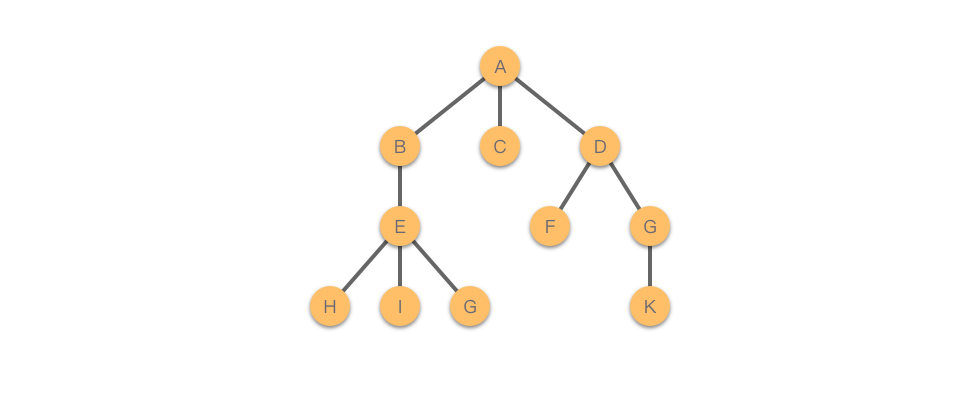
Cây có các đặc điểm sau:
- Chỉ có duy nhất một nút không có nút cha, nút này được gọi là nút gốc (root).
- Ngoại trừ nút gốc, mỗi nút chỉ có duy nhất một nút cha.
- Ngoại trừ nút gốc, mỗi nút có thể có nhiều nút con.
- Khi , ngoại trừ nút gốc, các nút khác có thể được chia thành tập hợp con không giao nhau , mỗi tập hợp con này lại là một cây và được gọi là cây con của gốc.
Ví dụ như hình dưới đây, nút màu đỏ A là nút gốc, ngoại trừ nút gốc, còn có 3 cây con không giao nhau , , .
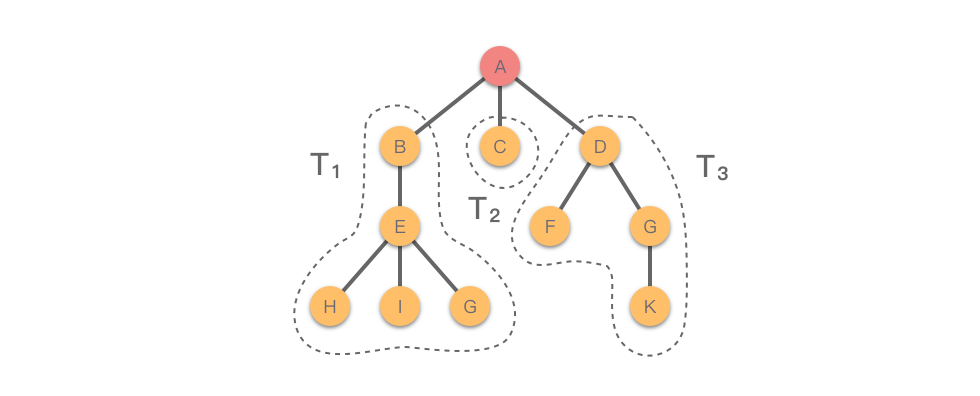
1.2 Các thuật ngữ liên quan đến cây
Dưới đây là một số thuật ngữ cơ bản liên quan đến cây.
1.2.1 Phân loại nút
Nút của cây bao gồm một phần tử dữ liệu và một số nhánh của cây trỏ đến các cây con của nút đó. Số lượng cây con mà nút có được gọi là độ của nút. Nút có độ bằng được gọi là nút lá hoặc nút cuối, nút có độ khác được gọi là nút nhánh hoặc nút không phải cuối. Độ lớn nhất của các nút trong cây được gọi là độ của cây.
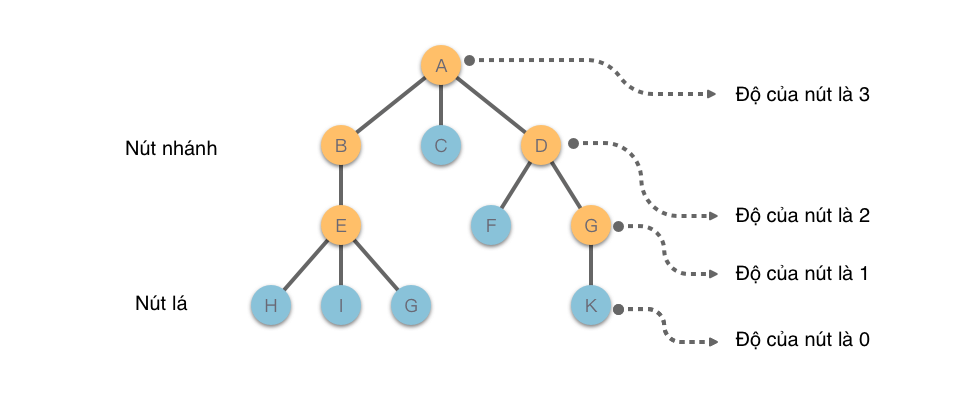
- Nút của cây: Bao gồm một phần tử dữ liệu và một số nhánh của cây trỏ đến các cây con của nút đó. Ví dụ như hình trên, nút của cây là
A,B,C,D,E,F,G,H,I,K. - Độ của nút: Số lượng cây con mà nút có. Ví dụ như hình trên, độ của nút
Alà . - Nút lá (nút cuối): Nút có độ bằng . Ví dụ như hình trên, các nút lá là
C,H,I,G,F,K. - Nút nhánh (nút không phải cuối): Nút có độ khác . Ví dụ như hình trên, các nút nhánh là
A,B,D,E,G. - Độ của cây: Độ lớn nhất của các nút trong cây. Ví dụ như hình trên, độ của cây là .
1.2.2 Mối quan hệ giữa các nút
Một nút con của một nút được gọi là nút con của nút đó, tương ứng, nút đó được gọi là nút cha của nút con đó. Các nút cùng cha được gọi là anh em của nhau.
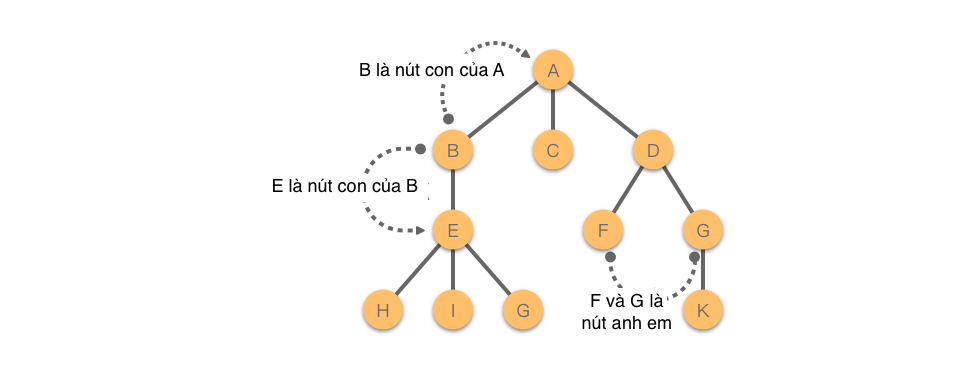
- Nút con (nút con): Nút con của một nút là nút con của nút đó. Ví dụ như hình trên,
Blà nút con củaA. - Nút cha (nút cha): Nếu một nút có nút con, thì nút đó được gọi là nút cha của nút con đó. Ví dụ như hình trên,
Blà nút cha củaE. - Anh em: Các nút có cùng nút cha được gọi là anh em của nhau. Ví dụ như hình trên,
FvàGlà anh em của nhau.
1.2.3 Các thuật ngữ khác của cây
Cấp của nút được định nghĩa từ nút gốc, nút gốc là cấp , nút con của nút gốc là cấp , và tiếp tục như vậy. Nút có cấp lớn nhất trong cây được gọi là độ sâu của cây hoặc độ cao của cây. Trong cây, chuỗi các nút mà chúng ta đi qua từ một nút đến một nút khác được gọi là đường đi, số lượng cạnh mà chúng ta đi qua giữa hai nút được gọi là độ dài của đường đi.
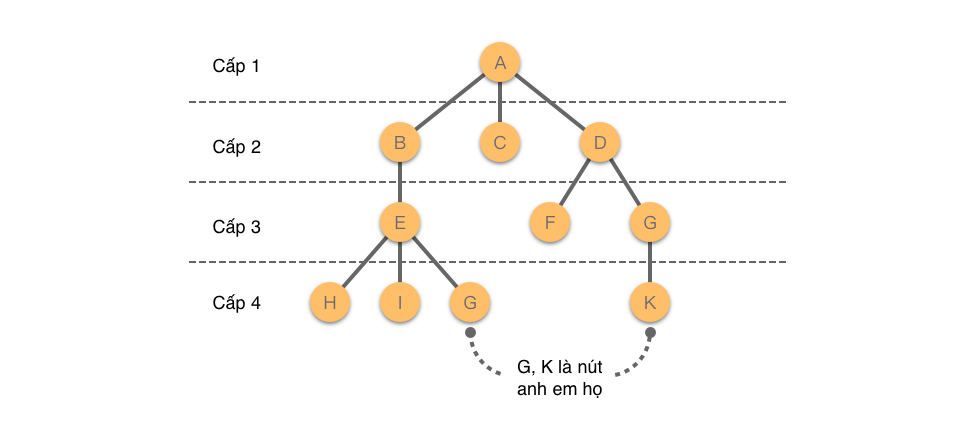
- Cấp của nút: Được định nghĩa từ nút gốc, nút gốc là cấp , nút con của nút gốc là cấp , và tiếp tục như vậy. Ví dụ như hình trên, cấp của nút
Elà . - Độ sâu của cây (độ cao của cây): Cấp lớn nhất của các nút trong cây. Ví dụ như hình trên, độ sâu của cây là .
- Nút anh em họ: Các nút có nút cha cùng cấp là anh em họ của nhau. Ví dụ:
GvàKtrong hình là các nút anh em họ của nhau. - Đường đi: Chuỗi các nút mà chúng ta đi qua từ một nút đến một nút khác được gọi là đường đi. Ví dụ như hình trên, đường đi từ
EđếnGlàE - B - A - D - G. - Độ dài của đường đi: Số lượng cạnh mà chúng ta đi qua giữa hai nút được gọi là độ dài của đường đi. Ví dụ như hình trên, độ dài của đường đi từ
EđếnGlà . - Tổ tiên của nút: Tất cả các nút mà chúng ta đi qua từ nút đó đến nút gốc được gọi là tổ tiên của nút đó. Ví dụ như hình trên, tổ tiên của nút
HlàE,B,A. - Con cháu của nút: Tất cả các nút trong cây con của nút đó được gọi là con cháu của nút đó. Ví dụ như hình trên, con cháu của nút
DlàF,G,K.
1.3 Phân loại cây
Dựa vào khả năng hoán đổi vị trí của các cây con của một nút, chúng ta có thể chia cây thành hai loại: cây có thứ tự và cây không có thứ tự.
Nếu các cây con của một nút được xem như có thứ tự từ trái sang phải (tức là không thể hoán đổi vị trí), thì cây đó được gọi là cây có thứ tự. Ngược lại, nếu các cây con của một nút có thể hoán đổi vị trí, thì cây đó được gọi là cây không có thứ tự.
- Cây có thứ tự: Các cây con của nút được sắp xếp từ trái sang phải theo một thứ tự cụ thể và không thể hoán đổi vị trí.
- Cây không có thứ tự: Các cây con của nút có thể hoán đổi vị trí với nhau.
2. Cây nhị phân
2.1 Định nghĩa cây nhị phân
Cây nhị phân (Binary Tree): Là một loại cây có thứ tự trong đó mỗi nút có tối đa
2nhánh. Cây nhị phân có thứ tự, với các nhánh được gọi là "cây con trái" và "cây con phải". Các nhánh của cây nhị phân có thứ tự và không thể hoán đổi vị trí.
Dưới đây là một ví dụ về cây nhị phân.
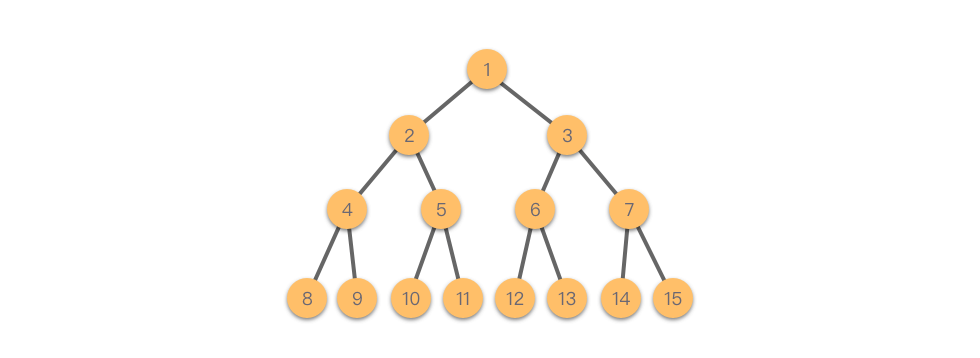
Cây nhị phân cũng có thể được định nghĩa bằng đệ quy, với hai yêu cầu sau:
- Cây rỗng: Cây nhị phân là một cây rỗng.
- Cây không rỗng: Cây nhị phân được tạo thành từ một nút gốc và hai cây con không giao nhau và , tương ứng là cây con trái và cây con phải của nút gốc; và , cũng là cây nhị phân.
Cây nhị phân là một loại cây đặc biệt, nó có tối đa hai cây con, mỗi cây con là cây con trái và cây con phải, và hai cây con này có thứ tự và không thể hoán đổi vị trí. Trong cây nhị phân, không có nút nào có độ lớn hơn 2.
Cây nhị phân có thể được chia thành hình dạng cơ bản từ một quan điểm logic, như hình dưới đây:
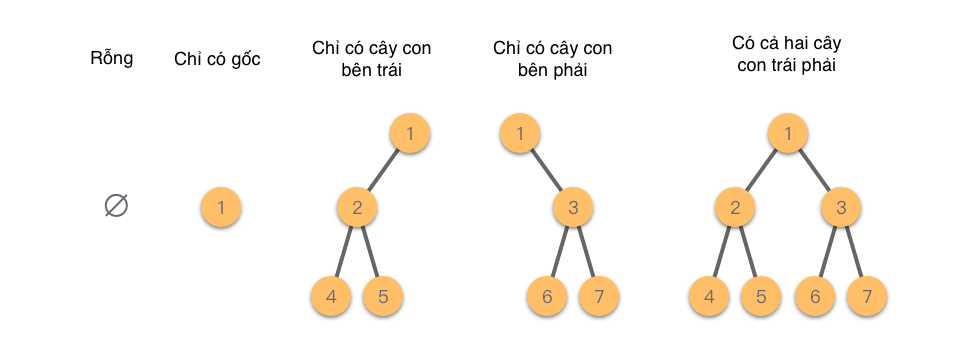
2.2 Các loại cây nhị phân đặc biệt
Dưới đây là một số loại cây nhị phân đặc biệt.
2.2.1 Cây nhị phân đầy đủ
Cây nhị phân đầy đủ (Full Binary Tree): Nếu tất cả các nút gốc đều có cả cây con trái và cây con phải, và tất cả các lá nằm ở cùng một mức, thì cây nhị phân đó được gọi là cây nhị phân đầy đủ.
Cây nhị phân đầy đủ có các đặc điểm sau:
- Các lá chỉ xuất hiện ở mức dưới cùng.
- Các nút không phải lá đều có độ là
2. - Trong các cây nhị phân cùng độ sâu, cây nhị phân đầy đủ có số nút và số lá lớn nhất.
Nếu chúng ta đánh số các nút của cây nhị phân đầy đủ, với nút gốc được đánh số là 1, sau đó theo thứ tự từ trên xuống dưới theo mức, từ trái sang phải, thì nút cuối cùng của cây nhị phân đầy đủ có độ sâu k sẽ có số hiệu là 2^k - 1.
Dưới đây là một số ví dụ về cây nhị phân đầy đủ.
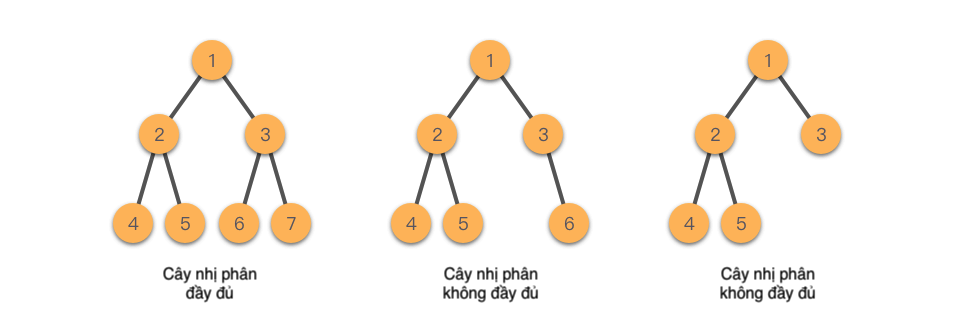
2.2.2 Cây nhị phân hoàn chỉnh
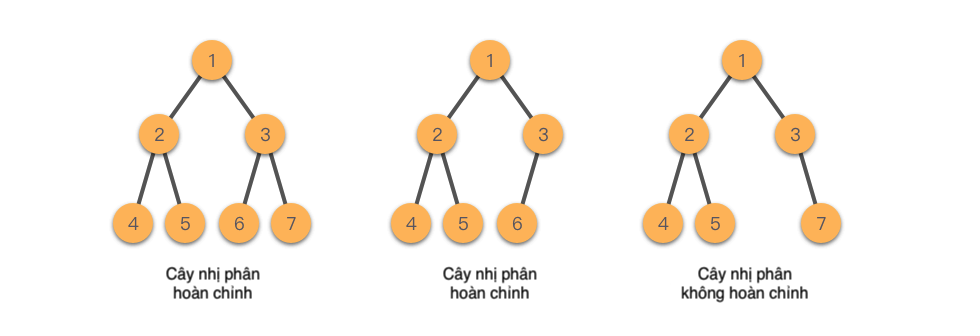
Cây nhị phân hoàn chỉnh (Complete Binary Tree): Nếu các lá chỉ xuất hiện ở hai mức dưới cùng và các lá ở mức dưới cùng được sắp xếp từ trái sang phải, thì cây nhị phân đó được gọi là cây nhị phân hoàn chỉnh.
Cây nhị phân hoàn chỉnh có các đặc điểm sau:
- Các lá chỉ xuất hiện ở hai mức dưới cùng.
- Các lá ở mức dưới cùng được sắp xếp từ trái sang phải.
- Nếu một nút có độ là
1, thì nút đó chỉ có thể có cây con trái, không thể chỉ có cây con phải. - Trong các cây nhị phân cùng số nút, cây nhị phân hoàn chỉnh có độ sâu nhỏ nhất.
Cây nhị phân hoàn chỉnh cũng có thể được định nghĩa bằng cách đánh số các nút, bắt đầu từ nút gốc với số hiệu là 1, sau đó theo thứ tự từ trên xuống dưới theo mức, từ trái sang phải. Đối với một cây nhị phân có độ sâu k và có n nút, chỉ khi mỗi nút tương ứng với một nút trong cây nhị phân đầy đủ với độ sâu k, và các nút được đánh số từ 1 đến n, thì cây nhị phân đó là cây nhị phân hoàn chỉnh.
Dưới đây là một số ví dụ về cây nhị phân hoàn chỉnh.
2.2.3 Cây nhị phân tìm kiếm
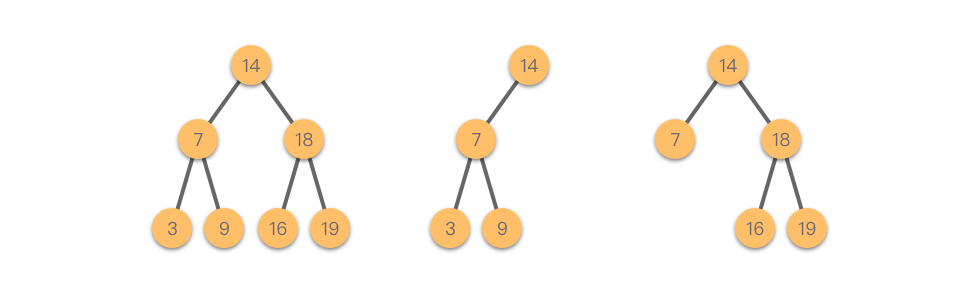
Cây nhị phân tìm kiếm (Binary Search Tree): Còn được gọi là cây tìm kiếm nhị phân, cây nhị phân có thứ tự hoặc cây nhị phân sắp xếp. Đây là một loại cây nhị phân có cấu trúc đặc biệt, trong đó mỗi nút có giá trị duy nhất và giá trị của nút con trái nhỏ hơn giá trị của nút cha, trong khi giá trị của nút con phải lớn hơn giá trị của nút cha.
Như hình dưới đây, ba cây đều là cây nhị phân tìm kiếm.
2.2.4 Cây nhị phân cân bằng
Cây nhị phân cân bằng (Balanced Binary Tree): Là một loại cây nhị phân tìm kiếm có cấu trúc cân bằng. Điều này có nghĩa là hiệu số tuyệt đối của độ sâu giữa các lá không vượt quá
1và cả hai cây con đều là cây nhị phân cân bằng. Cây nhị phân cân bằng có thể thực hiện các thao tác chèn, tìm kiếm và xóa trong thời gian. Cây nhị phân cân bằng đầu tiên được phát minh là 「cây AVL (Adelson-Velsky và Landis Tree)」.
Cây nhị phân cân bằng có các đặc điểm sau:
- Cây rỗng là một cây nhị phân cân bằng.
- Nếu T là một cây nhị phân cân bằng, thì cả hai cây con của nó cũng là cây nhị phân cân bằng và (ở đây là chiều cao của cây con trái, là chiều cao của cây con phải).
- Chiều cao của cây nhị phân cân bằng là .
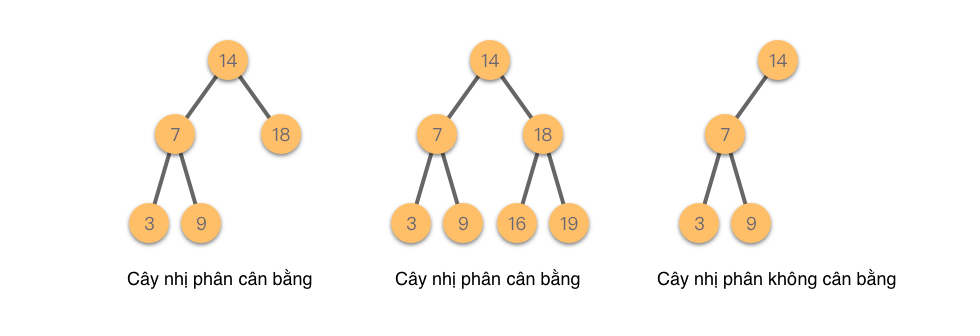
Như hình dưới đây, hai cây đầu tiên là cây nhị phân cân bằng, cây cuối cùng không phải là cây nhị phân cân bằng vì hiệu số tuyệt đối của độ sâu giữa các lá vượt quá 1.
2.3 Cấu trúc lưu trữ của cây nhị phân
Cây nhị phân có hai cấu trúc lưu trữ: "Cấu trúc lưu trữ theo thứ tự" và "Cấu trúc lưu trữ theo liên kết", dưới đây sẽ trình bày từng cấu trúc lưu trữ.
2.3.1 Cấu trúc lưu trữ theo tuần tự của cây nhị phân
Thực tế, cấu trúc heap trong thuật toán sắp xếp heap và hàng đợi ưu tiên sử dụng cấu trúc lưu trữ theo thứ tự của cây nhị phân.
Cấu trúc lưu trữ theo thứ tự của cây nhị phân sử dụng mảng một chiều để lưu trữ các nút của cây nhị phân, vị trí lưu trữ của nút được sắp xếp theo số thứ tự của nút trong cây nhị phân theo cấp số nhân, theo thứ tự từ trên xuống dưới và từ trái sang phải. Khi thực hiện lưu trữ theo thứ tự, nếu nút cây nhị phân tương ứng không tồn tại, thì được đặt là "nút rỗng".
Hình ảnh dưới đây là cấu trúc lưu trữ theo thứ tự của cây nhị phân.
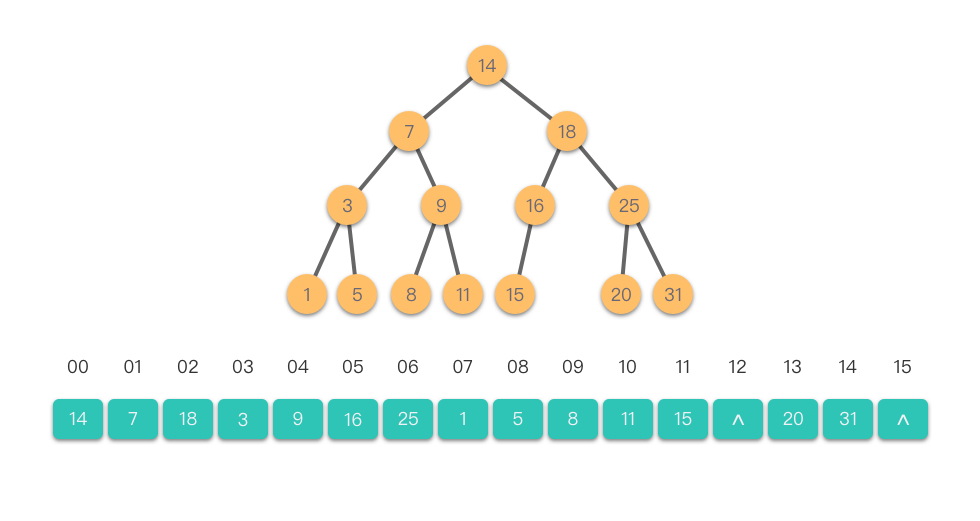
Từ hình ảnh, chúng ta cũng có thể thấy mối quan hệ logic giữa các nút.
- Nếu chỉ số của một nút cây nhị phân (không phải nút lá) là , thì chỉ số của nút con trái là , chỉ số của nút con phải là .
- Nếu chỉ số của một nút cây nhị phân (không phải nút gốc) là , thì chỉ số của nút gốc là . biểu thị phép chia lấy phần nguyên.
Đối với cây nhị phân đầy đủ (đặc biệt là cây nhị phân đầy đủ), cấu trúc lưu trữ theo thứ tự là phù hợp, nó có thể tận dụng tối đa không gian lưu trữ; đối với cây nhị phân thông thường, nếu cần thiết phải đặt nhiều "nút rỗng", thì cấu trúc lưu trữ theo thứ tự sẽ lãng phí nhiều không gian lưu trữ. Hơn nữa, do một số khuyết điểm cố định của cấu trúc lưu trữ theo thứ tự, các hoạt động như chèn, xóa trong cây nhị phân cũng không thuận tiện, hiệu suất cũng thấp. Đối với cây nhị phân, khi hình dạng và kích thước của cây thường thay đổi động, cấu trúc lưu trữ theo liên kết sẽ phù hợp hơn.
2.3.2 Cấu trúc lưu trữ theo liên kết của cây nhị phân
Khi cây nhị phân sử dụng cấu trúc lưu trữ theo liên kết, mỗi nút liên kết bao gồm một trường dữ liệu val, lưu trữ thông tin của nút; cũng như hai trường con trỏ left và right, lần lượt trỏ đến hai nút con trái và phải. Khi không có nút con trái hoặc nút con phải, giá trị của trường con trỏ tương ứng sẽ là rỗng.
Mã của cấu trúc liên kết của nút cây nhị phân như sau:
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = rightDưới đây, chúng ta sẽ sử dụng cấu trúc lưu trữ theo liên kết để lưu trữ cây nhị phân có giá trị là 1, 2, 3, 4, 5, 6, 7, như hình ảnh dưới đây.
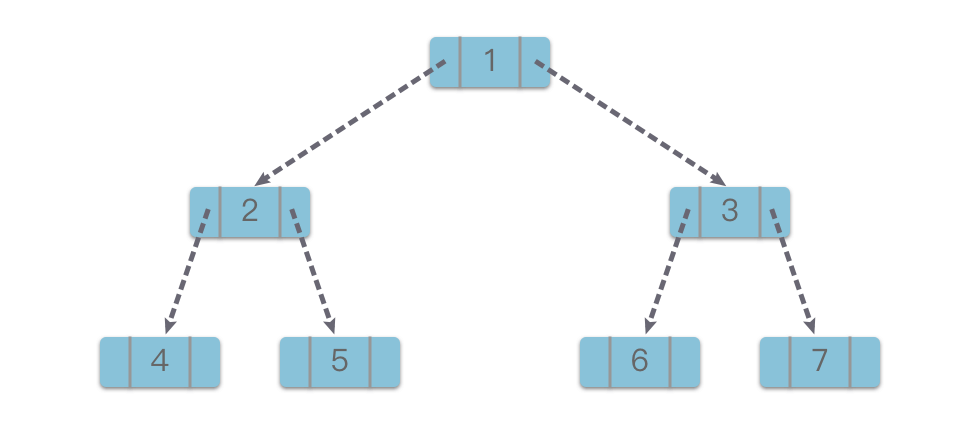
Cấu trúc lưu trữ theo liên kết của cây nhị phân có tính linh hoạt và tiện lợi. Số lượng nút tối đa chỉ phụ thuộc vào giới hạn không gian lưu trữ tối đa của hệ thống. Nói chung, cấu trúc lưu trữ theo liên kết của cây nhị phân tiết kiệm không gian hơn (chi phí không gian để lưu trữ trường con trỏ chỉ là một hàm tuyến tính của số lượng nút trong cây nhị phân), và cũng thuận tiện để thực hiện các hoạt động liên quan đến cây nhị phân, do đó, chúng ta thường sử dụng cấu trúc lưu trữ theo liên kết để lưu trữ cây nhị phân.