Topological Sorting

1. Giới thiệu về sắp xếp topo

Sắp xếp topo (Topological Sorting): Là phương pháp sắp xếp tuyến tính các đỉnh của đồ thị có hướng không chu trình (DAG), sao cho đối với mọi cặp đỉnh $u$ và $v$ , nếu có cạnh hướng từ $u$ đến $v$ , thì $u$ phải xuất hiện trước $v$ . Chuỗi tuyến tính của các đỉnh của đồ thị sau khi sắp xếp topo được gọi là sắp xếp topo.

Sắp xếp topo áp dụng cho đồ thị có hướng không chu trình (DAG), không áp dụng cho đồ thị vô hướng và đồ thị có hướng có chu trình.

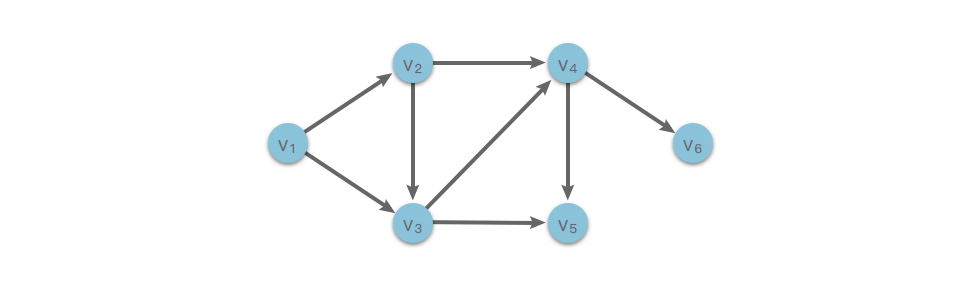
Như hình trên là một ví dụ về đồ thị có hướng không chu trình (DAG), $v_1 \rightarrow v_2 \rightarrow v_3 \rightarrow v_4 \rightarrow v_5 \rightarrow v_6$ là một chuỗi sắp xếp topo của đồ thị này. Đồng thời, $v_1 \rightarrow v_2 \rightarrow v_3 \rightarrow v_4 \rightarrow v_6 \rightarrow v_5$ cũng là một chuỗi sắp xếp topo của đồ thị này. Tức là đối với một đồ thị có hướng không chu trình, có thể có nhiều chuỗi sắp xếp topo.

2. Cách triển khai sắp xếp topo

Sắp xếp topo có hai phương pháp triển khai, đó là "Thuật toán Kahn" và "Thuật toán DFS tìm kiếm theo chiều sâu". Tiếp theo chúng ta sẽ đi xem cách thức triển khai của từng phương pháp.

2.1 Thuật toán Kahn

Ý tưởng cơ bản của thuật toán Kahn:
Liên tục tìm các đỉnh có bậc vào bằng $0$ trong đồ thị có hướng, và đưa chúng ra.
Sau đó xóa các đỉnh có bậc vào bằng $0$ và các cạnh có hướng xuất phát từ các đỉnh đó.
Lặp lại quá trình trên cho đến khi đồ thị trống hoặc không tìm thấy đỉnh có bậc vào bằng $0$ nào.

2.1.1 Các bước triển khai của thuật toán Kahn

Sử dụng mảng $indegrees$ để ghi nhận bậc vào của các đỉnh trong đồ thị.
Duy trì một tập hợp các đỉnh có bậc vào bằng $0$ ( $S$ ) (có thể sử dụng stack, queue, priority queue).
Mỗi lần lấy ra một đỉnh không có đỉnh tiền nhiệm (tức bậc vào bằng $0$ ) từ tập hợp, đưa nó vào chuỗi sắp xếp topo ( $order$ ).
Xóa đỉnh đó khỏi đồ thị và xóa các cạnh có hướng xuất phát từ đỉnh đó. Nếu bậc vào của đỉnh kết thúc là $0$ , đưa đỉnh đó vào tập hợp $S$ .
Lặp lại quá trình trên cho đến khi tập hợp $S$ trống hoặc còn đỉnh trong đồ thị chưa được duyệt qua (đồng nghĩa với việc tồn tại chu trình, không thể tạo thành chuỗi sắp xếp topo).
Nếu không tồn tại chu trình, thì thứ tự các đỉnh trong $order$ chính là kết quả của sắp xếp topo.

2.1.2 Code triển khai thuật toán Kahn

import collections

class Solution:
    # Sắp xếp topo, đồ thị chứa tất cả các cạnh hướng của các đỉnh (bao gồm cả đỉnh không có cạnh)
    def topologicalSortingKahn(self, graph: dict):
        indegrees = {u: 0 for u in graph}   # indegrees dùng để ghi nhận bậc vào của các đỉnh
        for u in graph:
            for v in graph[u]:
                indegrees[v] += 1           # Đếm số lượng đỉnh vào của tất cả các đỉnh
        
        # Đưa các đỉnh có bậc vào bằng 0 vào tập hợp S
        S = collections.deque([u for u in indegrees if indegrees[u] == 0])
        order = []                          # order dùng để lưu chuỗi sắp xếp topo
        
        while S:
            u = S.pop()                     # Lấy ra một đỉnh không có đỉnh tiền nhiệm
            order.append(u)                 # Đưa đỉnh đó vào chuỗi sắp xếp topo order
            for v in graph[u]:              # Duyệt qua các đỉnh kề v của đỉnh u
                indegrees[v] -= 1           # Xóa cạnh hướng xuất phát từ đỉnh u
                if indegrees[v] == 0:       # Nếu bậc vào của đỉnh v kết thúc là 0
                    S.append(v)             # Đưa đỉnh v vào tập hợp S
        
        if len(indegrees) != len(order):    # Còn đỉnh chưa duyệt qua (tồn tại chu trình), không thể tạo thành chuỗi sắp xếp topo
            return []
        return order                        # Trả về chuỗi sắp xếp topo
    
    
    def findOrder(self, n: int, edges):
        # Xây dựng đồ thị
        graph = dict()
        for i in range(n):
            graph[i] = []
            
        for u, v in edges:
            graph[u].append(v)
            
        return self.topologicalSortingKahn(graph)

2.2 Thuật toán sắp xếp topo dựa trên DFS

Ý tưởng cơ bản của thuật toán sắp xếp topo dựa trên DFS:
Đối với mỗi đỉnh $u$ , ta triển khai duyệt theo chiều sâu từ đỉnh đó theo các cạnh hướng $<u, v>$ . Nếu tất cả các đỉnh kề $v$ của đỉnh $u$ đã được duyệt qua, thì khi quay lại đỉnh $u$ , đỉnh $u$ phải đứng trước tất cả các đỉnh kề $v$ của nó trong chuỗi sắp xếp topo.
Như vậy, khi ta duyệt qua mỗi đỉnh và triển khai duyệt theo chiều sâu, ta sẽ đưa đỉnh đó vào stack. Cuối cùng, từ đỉnh đầu stack đến đỉnh cuối stack sẽ là một chuỗi sắp xếp topo.

2.2.1 Các bước triển khai của thuật toán sắp xếp topo dựa trên DFS

Sử dụng tập hợp $visited$ để ghi nhận xem đỉnh hiện tại đã được duyệt qua hay chưa, tránh việc duyệt qua lại.
Sử dụng tập hợp $onStack$ để ghi nhận xem đỉnh hiện tại đã được duyệt qua trong cùng một lần duyệt theo chiều sâu hay chưa. Nếu đỉnh hiện tại đã được duyệt qua trong cùng một lần duyệt theo chiều sâu, có nghĩa là đồ thị có chu trình và không thể tạo thành chuỗi sắp xếp topo.
Sử dụng biến boolean $hasCycle$ để kiểm tra xem đồ thị có chu trình hay không.
Bắt đầu từ một đỉnh chưa được duyệt qua.
1. Nếu đỉnh hiện tại đã được duyệt qua trong cùng một lần duyệt theo chiều sâu, có nghĩa là đồ thị có chu trình.
2. Nếu đỉnh hiện tại đã được duyệt qua hoặc có chu trình, không cần tiếp tục duyệt, trả về kết quả.
Đánh dấu đỉnh hiện tại là đã được duyệt qua và đã được duyệt qua trong cùng một lần duyệt theo chiều sâu. Sau đó, duyệt theo chiều sâu từ đỉnh hiện tại theo các cạnh hướng $<u, v>$ .
Khi tất cả các đỉnh kề $v$ của đỉnh hiện tại $u$ đã được duyệt qua, quay lại đỉnh $u$ và đưa đỉnh $u$ vào stack.
Hủy đánh dấu đỉnh hiện tại đã được duyệt qua trong cùng một lần duyệt theo chiều sâu.
Lặp lại các bước $4 \sim 7$ cho tất cả các đỉnh chưa được duyệt qua, cho đến khi tất cả các đỉnh đã được duyệt qua hoặc có chu trình.
Nếu không có chu trình, đảo ngược stack và lấy các đỉnh từ đỉnh đầu stack đến đỉnh cuối stack, kết quả chính là chuỗi sắp xếp topo.

2.2.2 Code triển khai thuật toán sắp xếp topo dựa trên DFS

import collections

class Solution:
    # Sắp xếp topo, đồ thị chứa tất cả các cạnh hướng của các đỉnh (bao gồm cả đỉnh không có cạnh)
    def topologicalSortingDFS(self, graph: dict):
        visited = set()                     # Ghi nhận xem đỉnh đã được duyệt qua hay chưa
        onStack = set()                     # Ghi nhận xem đỉnh đã được duyệt qua trong cùng một lần duyệt theo chiều sâu hay chưa
        order = []                          # Dùng để lưu chuỗi sắp xếp topo
        hasCycle = False                    # Kiểm tra xem đồ thị có chu trình hay không
        
        def dfs(u):
            nonlocal hasCycle
            if u in onStack:                # Nếu đỉnh đã được duyệt qua trong cùng một lần duyệt theo chiều sâu, có nghĩa là đồ thị có chu trình
                hasCycle = True
            if u in visited or hasCycle:    # Nếu đỉnh đã được duyệt qua hoặc có chu trình, không cần tiếp tục duyệt, trả về kết quả
                return
            
            visited.add(u)                  # Đánh dấu đỉnh đã được duyệt qua
            onStack.add(u)                  # Đánh dấu đỉnh đã được duyệt qua trong cùng một lần duyệt theo chiều sâu
    
            for v in graph[u]:              # Duyệt qua các đỉnh kề v của đỉnh u
                dfs(v)                      # Duyệt theo chiều sâu đỉnh v
                    
            order.append(u)                 # Đưa đỉnh u vào stack
            onStack.remove(u)               # Hủy đánh dấu đỉnh đã được duyệt qua trong cùng một lần duyệt theo chiều sâu
        
        for u in graph:
            if u not in visited:
                dfs(u)                      # Duyệt qua các đỉnh chưa được duyệt qua
        
        if hasCycle:                        # Kiểm tra xem có chu trình hay không
            return []                       # Có chu trình, không thể tạo thành chuỗi sắp xếp topo
        order.reverse()                     # Đảo ngược stack và lấy các đỉnh từ đỉnh đầu stack đến đỉnh cuối stack
        return order                        # Trả về chuỗi sắp xếp topo
    
    def findOrder(self, n: int, edges):
        # Xây dựng đồ thị
        graph = dict()
        for i in range(n):
            graph[i] = []
        for v, u in edges:
            graph[u].append(v)
        
        return self.topologicalSortingDFS(graph)

3. Ứng dụng của sắp xếp topo

Sắp xếp topo có thể được sử dụng để giải quyết một số vấn đề liên quan đến sự phụ thuộc, như thứ tự thực hiện dự án, thứ tự chọn môn học, v.v.

3.1 Bảng môn học II

3.1.1 Liên kết đề bài

210. Course Schedule II

3.1.2 Tóm tắt đề bài

Mô tả: Cho một số nguyên $numCourses$ , đại diện cho số lượng môn học phải chọn trong học kỳ này, các môn học được đánh số từ $0$ đến $numCourses - 1$ . Cho một mảng $prerequisites$ biểu thị mối quan hệ tiên quyết giữa các môn học, trong đó $prerequisites[i] = [ai, bi]$ có nghĩa là để học môn $ai$ , phải hoàn thành môn $bi$ trước.

Yêu cầu: Trả về thứ tự học các môn để hoàn thành tất cả các môn học. Nếu có nhiều thứ tự đúng, chỉ cần trả về một trong số đó. Nếu không thể hoàn thành tất cả các môn học, trả về một mảng rỗng.

Giải thích:

Ví dụ 1:

Input: numCourses = 2, prerequisites = [[1,0]]
Output: [0,1]
Explanation: Tổng cộng có 2 môn học. Để học môn 1, bạn phải hoàn thành môn 0 trước. Do đó, thứ tự học đúng là [0,1].

Ví dụ 2:

Input: numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
Output: [0,2,1,3]
Explanation: Tổng cộng có 4 môn học. Để học môn 3, bạn phải hoàn thành môn 1 và môn 2 trước. Và môn 1 và môn 2 phải được xếp sau môn 0. Do đó, một thứ tự học đúng là [0,1,2,3]. Một thứ tự học khác là [0,2,1,3].

3.1.3 Ý tưởng giải quyết

Ý tưởng 1: Sắp xếp topo

Bài toán này là phiên bản nâng cấp của bài toán "207. Course Schedule". Chỉ cần thêm một mảng $order$ để lưu trữ thứ tự học.

Sử dụng bảng băm $graph$ để lưu trữ đồ thị môn học và đếm số lượng đỉnh vào, lưu vào danh sách $indegrees$ .
Sử dụng hàng đợi $S$ để đưa tất cả các đỉnh có độ vào bằng $0$ vào hàng đợi.
Chọn một đỉnh $u$ từ hàng đợi và thêm nó vào mảng $order$ .
Xóa đỉnh $u$ khỏi đồ thị và xóa các cạnh đi ra từ đỉnh đó ( $<u, v>$ ). Nếu đỉnh $v$ có độ vào bằng $0$ sau khi xóa cạnh, thêm nó vào hàng đợi $S$ .
Lặp lại bước 3 và 4 cho đến khi hàng đợi không còn đỉnh nào.
Kiểm tra xem tổng số đỉnh và số đỉnh trong thứ tự topo có bằng nhau không. Nếu bằng nhau, trả về mảng $order$ , ngược lại, trả về một mảng rỗng.

Ý tưởng 1: Code

import collections

class Solution:
    # Sắp xếp topo, graph chứa tất cả các cạnh hướng (bao gồm các đỉnh không có cạnh)
    def topologicalSortingKahn(self, graph: dict):
        indegrees = {u: 0 for u in graph}   # indegrees dùng để lưu trữ độ vào của tất cả các đỉnh
        for u in graph:
            for v in graph[u]:
                indegrees[v] += 1           # Đếm số lượng đỉnh vào
        
        # Thêm các đỉnh có độ vào bằng 0 vào hàng đợi S
        S = collections.deque([u for u in indegrees if indegrees[u] == 0])
        order = []                          # order dùng để lưu trữ thứ tự topo
        
        while S:
            u = S.pop()                     # Chọn một đỉnh không có đỉnh tiền đề từ hàng đợi S
            order.append(u)                 # Thêm đỉnh vào thứ tự topo order
            for v in graph[u]:              # Duyệt qua các đỉnh kề v của đỉnh u
                indegrees[v] -= 1           # Xóa cạnh hướng từ đỉnh u
                if indegrees[v] == 0:       # Nếu sau khi xóa cạnh, đỉnh v có độ vào bằng 0
                    S.append(v)             # Thêm đỉnh vào hàng đợi S
        
        if len(indegrees) != len(order):    # Còn đỉnh chưa được duyệt (có chu trình), không thể tạo thành thứ tự topo
            return []
        return order                        # Trả về thứ tự topo
    
    
    def findOrder(self, numCourses: int, prerequisites):
        graph = dict()
        for i in range(numCourses):
            graph[i] = []
            
        for v, u in prerequisites:
            graph[u].append(v)
            
        return self.topologicalSortingKahn(graph)

Ý tưởng 1: Phân tích độ phức tạp

Độ phức tạp thời gian: $O(n + m)$ , trong đó $n$ là số lượng môn học và $m$ là số lượng yêu cầu tiên quyết.
Độ phức tạp không gian: $O(n + m)$ .

3.2 Tìm trạng thái an toàn cuối cùng

3.2.1 Liên kết đề bài

802. Find Eventual Safe States

3.2.2 Tóm tắt đề bài

Mô tả: Cho một đồ thị có hướng $graph$ , trong đó $graph[i]$ là danh sách các đỉnh kề với đỉnh $i$ , có nghĩa là từ đỉnh $i$ có một cạnh đi đến mỗi đỉnh trong $graph[i]$ .

Yêu cầu: Tìm tất cả các đỉnh an toàn trong đồ thị và trả về chúng dưới dạng một mảng được sắp xếp theo thứ tự tăng dần.

Giải thích:

Đỉnh cuối: Nếu một đỉnh không có cạnh đi ra, thì nó là đỉnh cuối. Nghĩa là, nếu không có cạnh đi ra, thì đỉnh đó là đỉnh cuối.
Đỉnh an toàn: Nếu tất cả các đường đi có thể từ đỉnh đó đến đỉnh cuối, thì đỉnh đó là đỉnh an toàn.
$n == graph.length$ .
$1 \le n \le 10^4$ .
$0 \le graph[i].length \le n$ .
$0 \le graph[i][j] \le n - 1$ .
$graph[i]$ được sắp xếp theo thứ tự tăng dần.
Đồ thị có thể chứa các chu trình.
Số cạnh trong đồ thị nằm trong khoảng $[1, 4 \times 10^4]$ .

Ví dụ:

Ví dụ 1:

Đầu vào: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Đầu ra: [2,4,5,6]
Giải thích: Như hình minh họa.
Đỉnh 5 và đỉnh 6 là đỉnh cuối vì chúng không có cạnh đi ra.
Tất cả các đường đi từ đỉnh 2, 4, 5 và 6 đều dẫn đến đỉnh 5 hoặc 6.

Ví dụ 2:

Đầu vào: graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
Đầu ra: [4]
Giải thích:
Chỉ có đỉnh 4 là đỉnh cuối, tất cả các đường đi từ đỉnh 4 đều dẫn đến đỉnh 4.

3.2.3 Ý tưởng giải quyết

Ý tưởng 1: Sắp xếp topo

Dựa vào yêu cầu đề bài, các đỉnh an toàn tương ứng với các đỉnh cuối có bậc ra bằng 0. Đồng thời, các đỉnh an toàn đều không thuộc chu trình.
Chúng ta có thể sử dụng thuật toán sắp xếp topo để kiểm tra xem một đỉnh có thuộc chu trình hay không.
Để tìm các đỉnh an toàn, chúng ta có thể sử dụng cách xây dựng đồ thị ngược. Điều này có nghĩa là chúng ta đảo ngược tất cả các cạnh trong đồ thị ban đầu. Điều này sẽ biến các đỉnh cuối có bậc ra bằng 0 thành các đỉnh có bậc vào bằng 0.
Sau đó, chúng ta sử dụng thuật toán sắp xếp topo để loại bỏ các đỉnh có bậc vào bằng 0. Nếu một đỉnh không thuộc chu trình, thì cuối cùng bậc vào của nó sẽ bằng 0. Các đỉnh này chính là các đỉnh an toàn. Các đỉnh thuộc chu trình sẽ có bậc vào khác 0.
Cuối cùng, chúng ta lưu trữ tất cả các đỉnh an toàn vào một mảng và trả về mảng đó.

Ý tưởng 1: Code

class Solution:
    # Sắp xếp topo, graph chứa tất cả các cạnh hướng của các đỉnh (bao gồm cả đỉnh không có cạnh)
    def topologicalSortingKahn(self, graph: dict):
        indegrees = {u: 0 for u in graph}   # indegrees dùng để ghi nhận bậc vào của tất cả các đỉnh
        for u in graph:
            for v in graph[u]:
                indegrees[v] += 1           # Đếm số lượng cạnh vào của tất cả các đỉnh
        
        # Đưa các đỉnh có bậc vào bằng 0 vào tập hợp S
        S = collections.deque([u for u in indegrees if indegrees[u] == 0])
        
        while S:
            u = S.pop()                     # Chọn một đỉnh không có đỉnh tiền nhiệm trong tập hợp S
            for v in graph[u]:              # Duyệt qua các đỉnh kề v của đỉnh u
                indegrees[v] -= 1           # Xóa cạnh hướng từ đỉnh u đến đỉnh v
                if indegrees[v] == 0:       # Nếu sau khi xóa cạnh đó, bậc vào của đỉnh v trở thành 0
                    S.append(v)             # Đưa đỉnh v vào tập hợp S
        
        res = []
        for u in indegrees:
            if indegrees[u] == 0:
                res.append(u)
        
        return res
        
    def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:
        graph_dict = {u: [] for u in range(len(graph))}

        for u in range(len(graph)):
            for v in graph[u]:
                graph_dict[v].append(u)     # Xây dựng đồ thị ngược

        return self.topologicalSortingKahn(graph_dict)

Ý tưởng 1: Phân tích độ phức tạp

Độ phức tạp thời gian: $O(n + m)$ , trong đó $n$ là số lượng đỉnh trong đồ thị, $m$ là số lượng cạnh trong đồ thị.
Độ phức tạp không gian: $O(n + m)$ .