Skip to main content

BFS

Hung NguyenAbout 8 minalgorithmalgorithm

1. Giới thiệu về thuật toán Tìm kiếm theo Chiều Rộng

Thuật toán Tìm kiếm theo Chiều Rộng (Breadth First Search): viết tắt là BFS, là một thuật toán được sử dụng để tìm kiếm trong cây hoặc đồ thị. Thuật toán BFS bắt đầu từ nút khởi đầu, mở rộng theo từng tầng, trước tiên duyệt các nút gần nút khởi đầu nhất, sau đó duyệt các nút xa nút khởi đầu hơn. Tiếp tục quá trình này cho đến khi hoàn thành toàn bộ quá trình tìm kiếm.

Vì thứ tự các nút được duyệt tuân theo nguyên tắc "trước vào trước ra", nên thuật toán Tìm kiếm theo Chiều Rộng có thể được thực hiện bằng cách sử dụng "hàng đợi".

2. Các bước của thuật toán Tìm kiếm theo Chiều Rộng

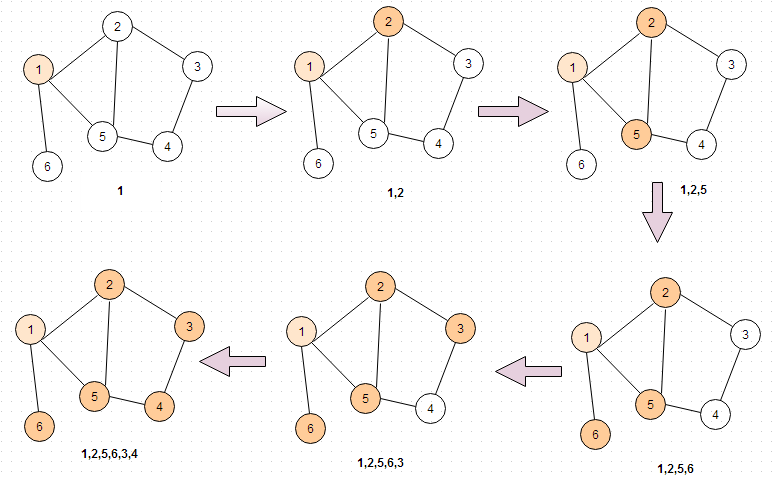
Tiếp theo, chúng ta sẽ lấy một đồ thị vô hướng làm ví dụ để giới thiệu các bước của thuật toán Tìm kiếm theo Chiều Rộng.

  1. Đưa nút khởi đầu uu vào hàng đợi và đánh dấu là đã duyệt.
  2. Lấy một nút từ hàng đợi, duyệt nút đó và đưa tất cả các nút kề chưa được duyệt vv vào hàng đợi.
  3. Đánh dấu nút vv đã duyệt để tránh việc duyệt lại.
  4. Lặp lại bước 2-3 cho đến khi hàng đợi trống hoặc tìm thấy nút mục tiêu.
image.png
image.png

3. Sử dụng hàng đợi để thực hiện tìm kiếm theo chiều rộng

3.1 Các bước của thuật toán tìm kiếm theo chiều rộng sử dụng hàng đợi

  1. Định nghĩa biến graphgraph để lưu trữ đồ thị vô hướng dưới dạng mảng lồng nhau, visitedvisited để đánh dấu các nút đã được duyệt, queuequeue để lưu trữ các nút trong hàng đợi, uu là nút bắt đầu, định nghĩa phương thức def bfs(graph, u): để thực hiện tìm kiếm theo chiều rộng sử dụng hàng đợi.
  2. Đầu tiên, đánh dấu nút bắt đầu uu là đã được duyệt và thêm nó vào hàng đợi, tức là visited.add(u) và queue.append(u).
  3. Lấy nút đầu hàng đợi uu. Duyệt qua nút uu và thực hiện các thao tác liên quan (tuỳ thuộc vào yêu cầu cụ thể của bài toán).
  4. Duyệt qua tất cả các nút kề chưa được duyệt vv của nút uu (nút vv không có trong visitedvisited).
  5. Đánh dấu nút vv là đã được duyệt và thêm nó vào hàng đợi, tức là visited.add(v) và queue.append(v).
  6. Lặp lại các bước 3-5 cho đến khi hàng đợi queuequeue rỗng.

3.2 Code triển khai tìm kiếm theo chiều rộng sử dụng hàng đợi

import collections

class Solution:
    def bfs(self, graph, u):
        visited = set()                     # Sử dụng visited để đánh dấu các nút đã duyệt
        queue = collections.deque([])       # Sử dụng queue để lưu trữ các nút tạm thời
        
        visited.add(u)                      # Đánh dấu nút bắt đầu u là đã duyệt
        queue.append(u)                     # Thêm nút bắt đầu u vào hàng đợi
        
        while queue:                        # Hàng đợi không rỗng
            u = queue.popleft()             # Lấy nút đầu hàng đợi u
            print(u)                        # Duyệt nút u
            for v in graph[u]:              # Duyệt qua tất cả các nút kề chưa được duyệt v của nút u
                if v not in visited:        # Nút v chưa được duyệt
                    visited.add(v)          # Đánh dấu nút v là đã duyệt
                    queue.append(v)         # Thêm nút v vào hàng đợi
                

graph = {
    "0": ["1", "2"],
    "1": ["0", "2", "3"],
    "2": ["0", "1", "3", "4"],
    "3": ["1", "2", "4", "5"],
    "4": ["2", "3"],
    "5": ["3", "6"],
    "6": []
}

# Thực hiện tìm kiếm theo chiều rộng sử dụng hàng đợi
Solution().bfs(graph, "0")

4. Ứng dụng của thuật toán Tìm kiếm theo Chiều Rộng

4.1 Sao chép đồ thị

4.1.1 Liên kết đến bài toán

4.1.2 Ý tưởng

Mô tả: Cho một đồ thị vô hướng được biểu diễn dưới dạng danh sách kề (mảng 2 chiều) với adjList[i]adjList[i] là danh sách kề của nút có giá trị i+1i + 1, adjList[i][j]adjList[i][j] là nút kề với nút có giá trị i+1i + 1.

Yêu cầu: Trả về một bản sao sâu của đồ thị đó.

Giải thích:

  • Đồ thị có tối đa 100100 nút.
  • Mỗi giá trị nút Node.valNode.val là duy nhất, 1≤Node.val≤1001 \le Node.val \le 100.
  • Đồ thị vô hướng là một đồ thị đơn giản, điều này có nghĩa là không có cạnh trùng lặp và không có đỉnh tự vòng.
  • Vì đồ thị là vô hướng, nếu nút pp là hàng xóm của nút qq, thì nút qq cũng phải là hàng xóm của nút pp.
  • Đồ thị là đồ thị liên thông, bạn có thể truy cập tất cả các nút từ nút đã cho.

Ví dụ:

  • Ví dụ 1:
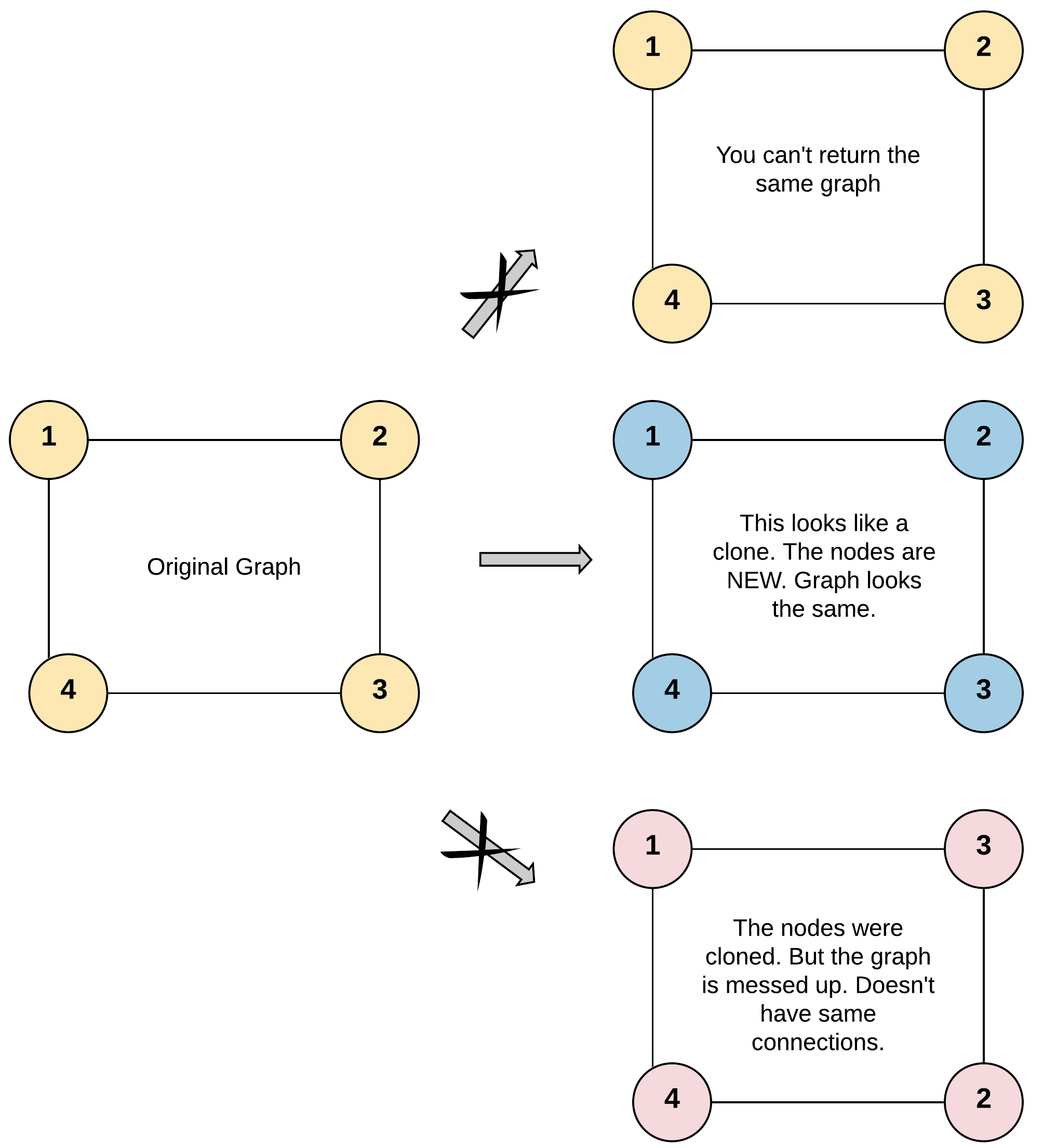
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation:
Có 4 nút trong đồ thị.
Nút 1 có giá trị là 1, có 2 hàng xóm: nút 2 và 4.
Nút 2 có giá trị là 2, có 2 hàng xóm: nút 1 và 3.
Nút 3 có giá trị là 3, có 2 hàng xóm: nút 2 và 4.
Nút 4 có giá trị là 4, có 2 hàng xóm: nút 1 và 3.
  • Ví dụ 2:
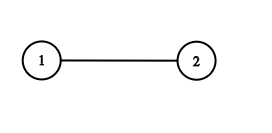
Input: adjList = [[2],[1]]
Output: [[2],[1]]

4.1.3 Ý tưởng giải quyết

Ý tưởng 1: Tìm kiếm theo Chiều Rộng
  1. Sử dụng bảng băm visitedvisited để lưu trữ các nút đã được duyệt trong đồ thị gốc và đồ thị sao chép, với cặp khóa-giá trị là "nút đã được duyệt trong đồ thị gốc: nút tương ứng trong đồ thị sao chép". Sử dụng hàng đợi queuequeue để lưu trữ các nút.
  2. Dựa trên nút bắt đầu nodenode, tạo một nút mới và thêm nó vào bảng băm visitedvisited, tức là visited[node] = Node(node.val, []). Sau đó, đưa nút bắt đầu vào hàng đợi, tức là queue.append(node).
  3. Lấy nút đầu hàng đợi nodeunode_u. Duyệt qua nút nodeunode_u và thực hiện các thao tác liên quan (tùy thuộc vào yêu cầu cụ thể của bài toán).
  4. Duyệt qua tất cả các nút kề chưa được duyệt nodevnode_v của nút nodeunode_u (nút nodevnode_v không có trong visitedvisited).
  5. Tạo một nút mới dựa trên nút nodevnode_v và thêm nó vào bảng băm visitedvisited, tức là visited[node_v] = Node(node_v.val, []).
  6. Sau đó, đưa nút nodevnode_v vào hàng đợi queuequeue, tức là queue.append(node_v).
  7. Lặp lại các bước 3-6 cho đến khi hàng đợi queuequeue rỗng.
  8. Kết thúc tìm kiếm theo chiều rộng, trả về nút sao chép của nút bắt đầu (tức là visited[node]visited[node]).
Ý tưởng 1: Code
class Solution:
    def cloneGraph(self, node: 'Node') -> 'Node':
        if not node:
            return node
        
        visited = dict()
        queue = collections.deque()

        visited[node] = Node(node.val, [])
        queue.append(node)

        while queue:
            node_u = queue.popleft()
            for node_v in node_u.neighbors:
                if node_v not in visited:
                    visited[node_v] = Node(node_v.val, [])
                    queue.append(node_v)
                visited[node_u].neighbors.append(visited[node_v])
        
        return visited[node]
Ý tưởng 1: Phân tích độ phức tạp
  • Độ phức tạp thời gian: O(n)O(n). Trong đó nn là số lượng nút trong đồ thị.
  • Độ phức tạp không gian: O(n)O(n).

4.2 Tìm diện tích lớn nhất của đảo

4.2.1 Liên kết đề bài

4.2.2 Đề bài

Mô tả: Cho một mảng hai chiều chứa các phần tử chỉ gồm 0 và 1, trong đó 1 đại diện cho đảo và 0 đại diện cho nước. Diện tích của một đảo chính là số lượng khối 1 kề cạnh theo chiều ngang hoặc chiều dọc.

Yêu cầu: Tính diện tích lớn nhất của đảo.

Giải thích:

  • mm là số hàng của mảng.
  • nn là số cột của mảng.
  • 1≤m,n≤501 \le m, n \le 50.
  • grid[i][j]grid[i][j] có giá trị 0 hoặc 1.

Ví dụ:

  • Ví dụ 1:
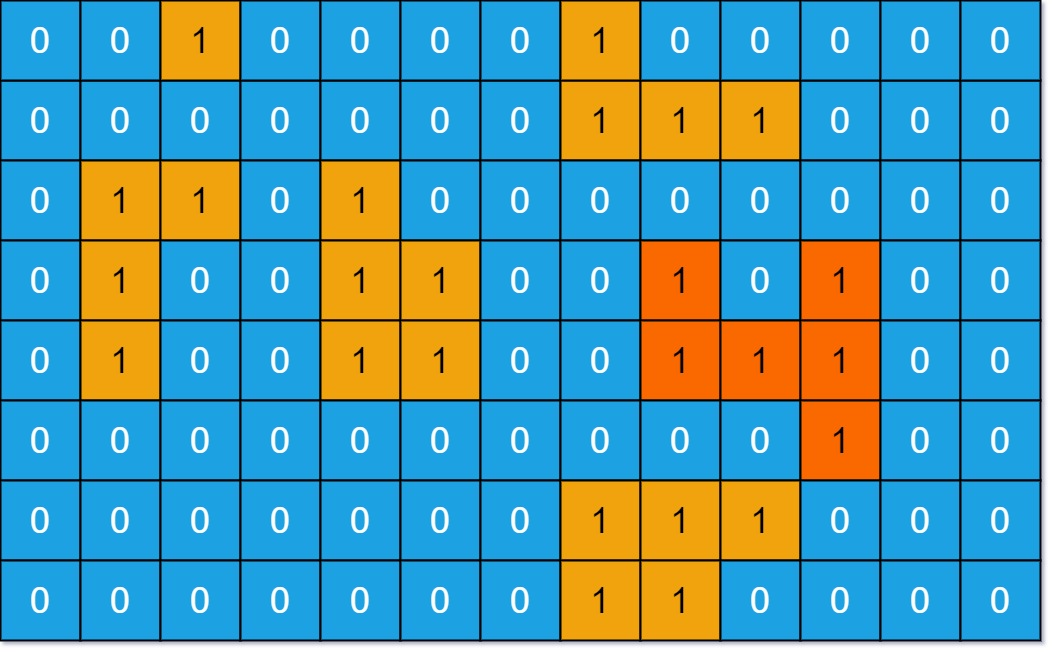
Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
Output: 6
Explanation: Đáp án không phải là 11, vì một đảo chỉ có thể chứa các khối 1 kề cạnh theo chiều ngang hoặc chiều dọc.
  • Ví dụ 2:
Input: grid = [[0,0,0,0,0,0,0,0]]
Output: 0

4.2.3 Ý tưởng giải quyết

Ý tưởng 1: Duyệt theo chiều rộng
  1. Sử dụng biến ansans để lưu diện tích lớn nhất của đảo.
  2. Duyệt qua từng phần tử trong mảng hai chiều, với mỗi phần tử có giá trị là 1:
    1. Đặt giá trị của phần tử đó thành 0. Sử dụng hàng đợi queuequeue để lưu vị trí của phần tử đó. Sử dụng biến temp‾anstemp\underline{}ans để lưu diện tích hiện tại của đảo.
    2. Lấy ra vị trí (i,j)(i, j) đầu tiên trong hàng đợi. Duyệt qua các vị trí lân cận trên, dưới, trái, phải của vị trí đó. Đặt giá trị của các vị trí lân cận thành 0 (để tránh duyệt lại). Thêm các vị trí lân cận vào hàng đợi. Tăng giá trị của temp‾anstemp\underline{}ans lên 1.
    3. Lặp lại bước trên cho đến khi hàng đợi queuequeue trống.
    4. Cập nhật diện tích lớn nhất của đảo, tức là ans=max⁡(ans,temp‾ans)ans = \max(ans, temp\underline{}ans).
  3. Trả về giá trị của ansans là kết quả.
Ý tưởng 1: Code
import collections

class Solution:
    def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
        directs = [(0, 1), (0, -1), (1, 0), (-1, 0)]
        rows, cols = len(grid), len(grid[0])
        ans = 0
        for i in range(rows):
            for j in range(cols):
                if grid[i][j] == 1:
                    grid[i][j] = 0
                    temp_ans = 1
                    queue = collections.deque([(i, j)])
                    while queue:
                        i, j = queue.popleft()
                        for direct in directs:
                            new_i = i + direct[0]
                            new_j = j + direct[1]
                            if new_i < 0 or new_i >= rows or new_j < 0 or new_j >= cols or grid[new_i][new_j] == 0:
                                continue
                            grid[new_i][new_j] = 0
                            queue.append((new_i, new_j))
                            temp_ans += 1

                    ans = max(ans, temp_ans)
        return ans
Ý tưởng 1: Phân tích độ phức tạp
  • Độ phức tạp thời gian: O(n×m)O(n \times m), trong đó mm và nn lần lượt là số hàng và số cột của mảng.
  • Độ phức tạp không gian: O(n×m)O(n \times m).
Made with ❤️ by Hung Nguyen
Copyright © 2016-2024 Hung Nguyen