Graph Structure

1. Cấu trúc lưu trữ đồ thị

Đồ thị có cấu trúc phức tạp, chúng ta cần biểu diễn các đỉnh và cạnh. Một đồ thị có thể có bất kỳ số lượng đỉnh nào (hữu hạn) và bất kỳ cặp đỉnh nào cũng có thể có cạnh. Khi triển khai cấu trúc lưu trữ đồ thị, chúng ta cần tập trung vào mối quan hệ giữa cạnh và đỉnh, đây là yếu tố quan trọng trong việc lưu trữ đồ thị.

Cấu trúc lưu trữ đồ thị có thể được thực hiện thông qua "cấu trúc lưu trữ tuần tự" và "cấu trúc lưu trữ liên kết". Các cấu trúc lưu trữ tuần tự bao gồm ma trận kề và mảng cạnh. Các cấu trúc lưu trữ liên kết bao gồm danh sách kề, danh sách liên kết tiến, danh sách liên kết chéo và danh sách liên kết đa.

Dưới đây là một số cấu trúc lưu trữ đồ thị phổ biến. Trong bài viết này, chúng ta sẽ sử dụng $n$ để biểu diễn số lượng đỉnh, $m$ để biểu diễn số lượng cạnh, $TD(v_i)$ để biểu diễn bậc của đỉnh $v_i$.

1.1 Ma trận kề

1.1.1 Mô tả lý thuyết về ma trận kề

Ma trận kề (Adjacency Matrix): Sử dụng một mảng hai chiều $adj\underline{}matrix$ để lưu trữ mối quan hệ kề giữa các đỉnh.

• Đối với đồ thị không có trọng số, nếu $adj\underline{}matrix[i][j]$ là $1$, thì có cạnh từ đỉnh $v_i$ đến $v_j$, nếu $adj\underline{}matrix[i][j]$ là $0$, thì không có cạnh từ đỉnh $v_i$ đến $v_j$.
• Đối với đồ thị có trọng số, nếu $adj\underline{}matrix[i][j]$ là $w$ và $w \ne \infty$ (tức là w != float('inf')), thì có cạnh từ đỉnh $v_i$ đến $v_j$ với trọng số là $w$. Nếu $adj\underline{}matrix[i][j]$ là $\infty$ (tức là float('inf')), thì không có cạnh từ đỉnh $v_i$ đến $v_j$.

Trong hình ví dụ dưới đây, bên trái là một đồ thị vô hướng và bên phải là cấu trúc ma trận kề tương ứng.

20220317144827.png

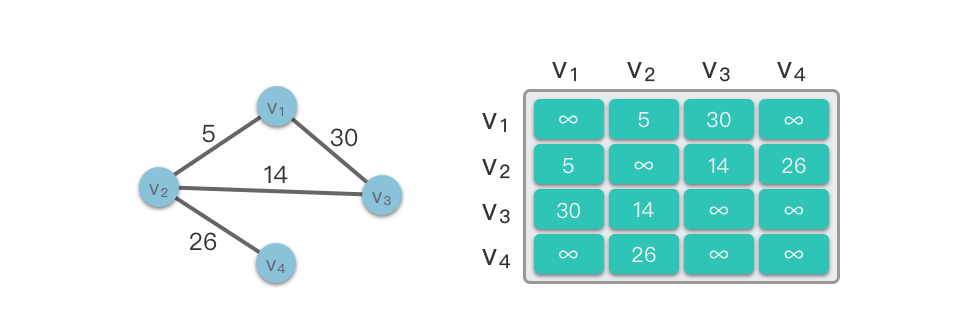
Đặc điểm của ma trận kề:

• Ưu điểm: Đơn giản trong việc triển khai và có thể truy vấn trực tiếp xem liệu có cạnh giữa đỉnh $v_i$ và $v_j$ hay không, cũng như truy vấn trọng số của cạnh.
• Nhược điểm: Hiệu suất khởi tạo và duyệt thấp, tốn nhiều không gian và không thể lưu trữ cạnh trùng lặp hoặc thêm/xóa nút một cách dễ dàng. Nếu số lượng đỉnh lớn (ví dụ $n > 10^5$), việc tạo ra một mảng hai chiều $n \times n$ không thực tế.

1.1.2 Phân tích thuật toán của ma trận kề

• Độ phức tạp thời gian:
  • Khởi tạo: $O(n^2)$.
  • Truy vấn, thêm hoặc xóa cạnh: $O(1)$.
  • Lấy tất cả các cạnh của một đỉnh: $O(n)$.
  • Duyệt đồ thị: $O(n^2)$.
• Độ phức tạp không gian: $O(n^2)$.

1.1.3 Triển khai mã của ma trận kề

class Graph:                                    # Lớp đồ thị cơ bản, sử dụng ma trận kề để biểu diễn
    # Khởi tạo đồ thị, ver_count là số lượng đỉnh
    def __init__(self, ver_count):
        self.ver_count = ver_count              # Số lượng đỉnh
        self.adj_matrix = [[None for _ in range(ver_count)] for _ in range(ver_count)]  # Ma trận kề
    
    # Kiểm tra tính hợp lệ của đỉnh v
    def __valid(self, v):
        return 0 <= v <= self.ver_count
    
    # Tạo đồ thị, edges là thông tin cạnh
    def creatGraph(self, edges=[]):
        for vi, vj, val in edges:
            self.add_edge(vi, vj, val)
    
    # Thêm cạnh vi - vj với trọng số val vào ma trận kề
    def add_edge(self, vi, vj, val):
        if not self.__valid(vi) or not self.__valid(vj):
            raise ValueError(str(vi) + ' hoặc ' + str(vj) + " không phải là đỉnh hợp lệ.")
        
        self.adj_matrix[vi][vj] = val
    
    # Lấy trọng số của cạnh vi - vj
    def get_edge(self, vi, vj):
        if not self.__valid(vi) or not self.__valid(vj):
            raise ValueError(str(vi) + ' hoặc ' + str(vj) + " không phải là đỉnh hợp lệ.")

        return self.adj_matrix[vi][vj]
    
    # In các cạnh của đồ thị dựa trên ma trận kề
    def printGraph(self):
        for vi in range(self.ver_count):
            for vj in range(self.ver_count):
                val = self.get_edge(vi, vj)
                if val:
                    print(str(vi) + ' - ' + str(vj) + ' : ' + str(val))
    

graph = Graph(5)
edges = [[1, 2, 5],[2, 1, 5],[1, 3, 30],[3, 1, 30],[2, 3, 14],[3, 2, 14],[2, 4, 26], [4, 2, 26]]
graph.creatGraph(edges)
print(graph.get_edge(3, 4))
graph.printGraph()

1.2 Mảng cạnh

1.2.1 Mô tả nguyên lý của mảng cạnh

Mảng cạnh (Edgeset Array): Sử dụng một mảng để lưu trữ mối quan hệ kề giữa các đỉnh. Mỗi phần tử trong mảng chứa điểm bắt đầu $v_i$, điểm kết thúc $v_j$ và trọng số của cạnh $val$ (nếu là đồ thị có trọng số).

Trong hình minh họa dưới đây, phía trái là một đồ thị có hướng và phía phải là cấu trúc mảng cạnh tương ứng với đồ thị đó.

20220317161454.png

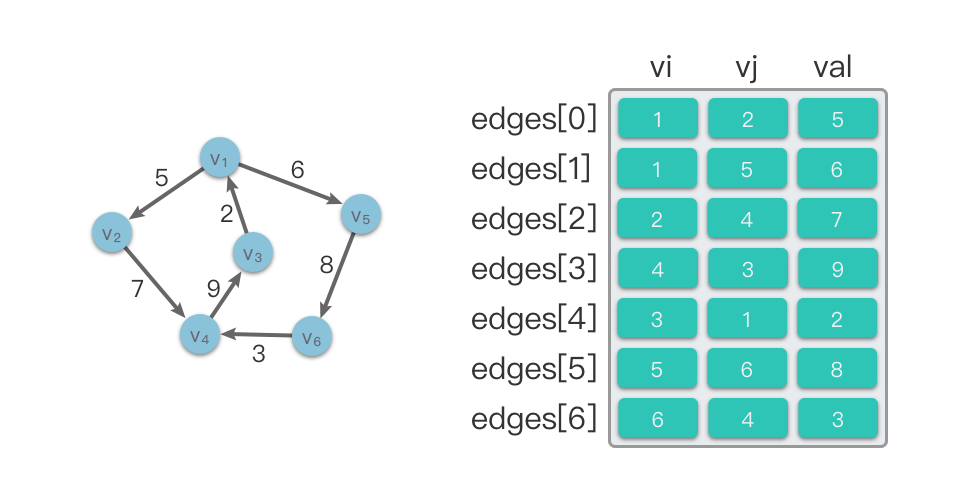
1.2.2 Phân tích thuật toán của mảng cạnh

Độ phức tạp thời gian của mảng cạnh:

• Khởi tạo và tạo đồ thị: $O(m)$.
• Kiểm tra xem một cạnh có tồn tại hay không: $O(m)$.
• Duyệt qua tất cả các cạnh của một đỉnh: $O(m)$.
• Duyệt qua toàn bộ đồ thị: $O(nm)$.

Độ phức tạp không gian của mảng cạnh:

• Độ phức tạp không gian: $O(m)$.

Khi tính toán bậc của một đỉnh hoặc tìm kiếm một cạnh cụ thể, cần duyệt qua toàn bộ mảng cạnh, độ phức tạp thời gian là $O(m)$, trong đó m là số lượng cạnh. Trừ khi cần thiết đặc biệt, hiếm khi sử dụng mảng cạnh để lưu trữ đồ thị.

Nói chung, mảng cạnh phù hợp cho các phép toán xử lý từng cạnh theo thứ tự, không phù hợp cho các phép toán xử lý đỉnh và các phép toán xử lý trên một cạnh bất kỳ.

1.2.3 Cài đặt mã của mảng cạnh

class EdgeNode:                                 # Lớp thông tin cạnh
    def __init__(self, vi, vj, val):
        self.vi = vi                            # Điểm bắt đầu của cạnh
        self.vj = vj                            # Điểm kết thúc của cạnh
        self.val = val                          # Trọng số của cạnh
        
class Graph:                                    # Lớp đồ thị cơ bản, sử dụng mảng cạnh để biểu diễn
    def __init__(self):
        self.edges = []                         # Mảng cạnh
        
    # Thực hiện tạo đồ thị, edges là thông tin cạnh
    def creatGraph(self, edges=[]):
        for vi, vj, val in edges:
            self.add_edge(vi, vj, val)
            
    # Thêm cạnh vi - vj với trọng số val vào mảng cạnh của đồ thị
    def add_edge(self, vi, vj, val):
        edge = EdgeNode(vi, vj, val)            # Tạo đối tượng cạnh
        self.edges.append(edge)                 # Thêm đối tượng cạnh vào mảng cạnh
        
    # Lấy trọng số của cạnh vi - vj
    def get_edge(self, vi, vj):
        for edge in self.edges:
            if vi == edge.vi and vj == edge.vj:
                val = edge.val
                return val
        return None
    
    # In đồ thị dựa trên mảng cạnh
    def printGraph(self):
        for edge in self.edges:
            print(str(edge.vi) + ' - ' + str(edge.vj) + ' : ' + str(edge.val))
            
graph = Graph()
edges = [[1, 2, 5],[1, 5, 6],[2, 4, 7],[4, 3, 9],[3, 1, 2],[5, 6, 8],[6, 4, 3]]
graph.creatGraph(edges)
print(graph.get_edge(3, 4))
graph.printGraph()

1.3 Danh sách kề

1.3.1 Mô tả nguyên lý của danh sách kề

Danh sách kề (Adjacency List): Sử dụng cấu trúc lưu trữ kết hợp giữa lưu trữ tuần tự và lưu trữ liên kết để lưu trữ thông tin về đỉnh và cạnh của đồ thị. Cấu trúc dữ liệu này bao gồm hai phần, một phần là mảng dùng để lưu trữ thông tin về các đỉnh, phần còn lại là danh sách liên kết dùng để lưu trữ thông tin về các cạnh.

Trong phương pháp lưu trữ danh sách kề, chúng ta tạo một danh sách liên kết tuyến tính cho mỗi đỉnh $v_i$ trong đồ thị, và liên kết tất cả các đỉnh kề với $v_i$ vào danh sách liên kết đó. Với đồ thị có n đỉnh, cấu trúc danh sách kề bao gồm n danh sách liên kết.

Sau đó, chúng ta sẽ tạo một nút đầu danh sách cho mỗi đỉnh, được gọi là "nút đỉnh". Mỗi nút đỉnh bao gồm "trường đỉnh" và "trường con trỏ", trong đó trường đỉnh được sử dụng để lưu trữ thông tin về một đỉnh cụ thể, và trường con trỏ được sử dụng để chỉ ra nút liên kết đầu tiên của đỉnh đó.

Để dễ dàng truy cập vào danh sách liên kết của bất kỳ đỉnh nào, thường chúng ta sẽ sử dụng một tập hợp cấu trúc lưu trữ tuần tự (mảng) để lưu trữ tất cả các phần tử "nút đỉnh", cấu trúc lưu trữ tuần tự (mảng) sẽ sắp xếp theo thứ tự của đỉnh trong đồ thị.

Trong hình minh họa dưới đây, phía trái là một đồ thị có hướng và phía phải là cấu trúc danh sách kề tương ứng với đồ thị đó.

20220317154531.png

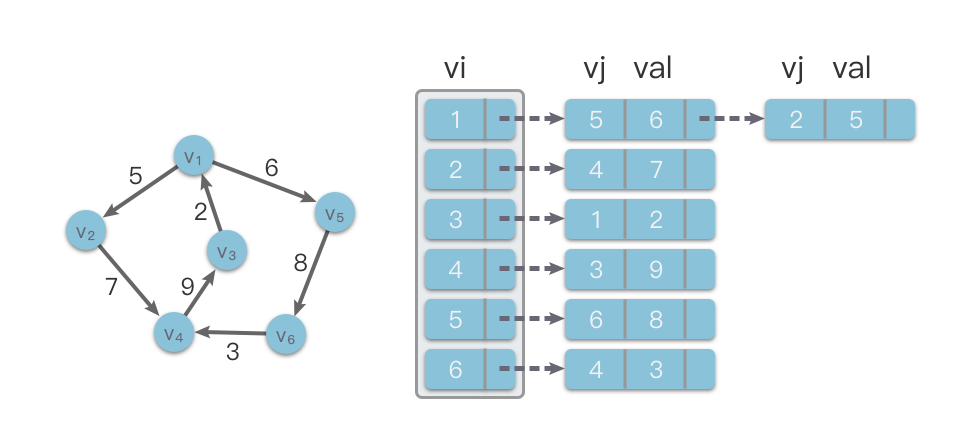
1.3.2 Phân tích thuật toán của danh sách kề

Độ phức tạp thời gian của danh sách kề:

• Khởi tạo và tạo đồ thị: $O(n + m)$.
• Kiểm tra xem có cạnh từ $v_i$ đến $v_j$ hay không: $O(TD(v_i))$.
• Duyệt qua tất cả các cạnh của một đỉnh: $O(TD(v_i))$.
• Duyệt qua toàn bộ đồ thị: $O(n + m)$.

Độ phức tạp không gian của danh sách kề:

• Độ phức tạp không gian: $O(n + m)$.

1.3.3 Cài đặt mã của danh sách kề

class EdgeNode:                                 # Lớp thông tin cạnh
    def __init__(self, vj, val):
        self.vj = vj                            # Điểm kết thúc của cạnh
        self.val = val                          # Trọng số của cạnh
        self.next = None                        # Cạnh tiếp theo

class VertexNode:                               # Lớp thông tin đỉnh
    def __init__(self, vi):
        self.vi = vi                            # Điểm bắt đầu của cạnh
        self.head = None                        # Đỉnh liên kết đầu tiên
        
class Graph:
    def __init__(self, ver_count):
        self.ver_count = ver_count
        self.vertices = []
        for vi in range(ver_count):
            vertex = VertexNode(vi)
            self.vertices.append(vertex)
    
    # Kiểm tra xem đỉnh v có hợp lệ không
    def __valid(self, v):
        return 0 <= v <= self.ver_count
    
    # Thực hiện tạo đồ thị, edges là thông tin cạnh
    def creatGraph(self, edges=[]):
        for vi, vj, val in edges:
            self.add_edge(vi, vj, val)
    
    # Thêm cạnh vi - vj với trọng số val vào danh sách kề của đồ thị
    def add_edge(self, vi, vj, val):
        if not self.__valid(vi) or not self.__valid(vj):
            raise ValueError(str(vi) + ' hoặc ' + str(vj) + " không phải là một đỉnh hợp lệ.")
            
        vertex = self.vertices[vi]
        edge = EdgeNode(vj, val)
        edge.next = vertex.head
        vertex.head = edge

    # Lấy trọng số của cạnh vi - vj
    def get_edge(self, vi, vj):
        if not self.__valid(vi) or not self.__valid(vj):
            raise ValueError(str(vi) + ' hoặc ' + str(vj) + " không phải là một đỉnh hợp lệ.")
        
        vertex = self.vertices[vi]
        cur_edge = vertex.head
        while cur_edge:
            if cur_edge.vj == vj:
                return cur_edge.val
            cur_edge = cur_edge.next
        return None
        
    # In các cạnh của đồ thị dựa trên danh sách kề
    def printGraph(self):
        for vertex in self.vertices:
            cur_edge = vertex.head
            while cur_edge:
                print(str(vertex.vi) + ' - ' + str(cur_edge.vj) + ' : ' + str(cur_edge.val))
                cur_edge = cur_edge.next
                
graph = Graph(7)
edges = [[1, 2, 5],[1, 5, 6],[2, 4, 7],[4, 3, 9],[3, 1, 2],[5, 6, 8],[6, 4, 3]]
graph.creatGraph(edges)
print(graph.get_edge(3, 4))
graph.printGraph()

1.4 Chuỗi liên kết đỉnh đầu

1.4.1 Mô tả nguyên lý của chuỗi liên kết đỉnh đầu

Chuỗi liên kết đỉnh đầu (Linked Forward Star): còn được gọi là bảng kề tĩnh, thực chất là một bảng kề được triển khai bằng cách sử dụng danh sách liên kết tĩnh. Chuỗi liên kết đỉnh đầu kết hợp mảng cạnh và bảng kề, cho phép truy cập nhanh đến tất cả các đỉnh kề của một đỉnh và sử dụng ít không gian bổ sung.

Chuỗi liên kết đỉnh đầu sử dụng cách lưu trữ danh sách liên kết tĩnh, có thể coi là cách lưu trữ hiệu quả nhất hiện nay cho việc xây dựng đồ thị và duyệt qua đồ thị.

Chuỗi liên kết đỉnh đầu bao gồm hai cấu trúc dữ liệu:

• Mảng cạnh đặc biệt: edges, trong đó edges[i] đại diện cho cạnh thứ i. edges[i].vj đại diện cho đỉnh kết thúc của cạnh thứ i, edges[i].val đại diện cho trọng số của cạnh thứ i, edges[i].next đại diện cho vị trí lưu trữ của cạnh tiếp theo có cùng đỉnh bắt đầu.
• Mảng đầu đỉnh: head, trong đó head[i] lưu trữ chỉ số của cạnh đầu tiên có đỉnh bắt đầu là i trong mảng cạnh edges.

Thực chất, chuỗi liên kết đỉnh đầu không thay đổi cách lưu trữ mảng cạnh ban đầu, chỉ sử dụng mảng head để tạo thành danh sách liên kết tĩnh, xác định mối quan hệ giữa đỉnh $v_i$ và cạnh đầu tiên kết nối với đỉnh $v_i$.

Trong hình minh họa dưới đây, phía trái là một đồ thị có hướng và phía phải là cấu trúc chuỗi liên kết đỉnh đầu tương ứng.

Nếu muốn duyệt qua tất cả các cạnh của đỉnh $v_1$ trong đồ thị này, các bước sẽ như sau:

• Tìm chỉ số của cạnh đầu tiên trong mảng cạnh edges mà có đỉnh bắt đầu là $v_1$, tức là index = head[1] = 1. Sau đó, tìm cạnh đầu tiên kết nối với đỉnh $v_1$ trong mảng edges là edges[1], tức là $\langle v_1, v_5 \rangle$ với trọng số là 6.
• Tiếp tục tìm index = self.edges[1].next = 0, sau đó tìm cạnh thứ hai kết nối với đỉnh $v_1$ trong mảng edges là edges[0], tức là $\langle v_1, v_2 \rangle$ với trọng số là 5.
• Tiếp tục tìm index = self.edges[0].next = -1, không có cạnh khác, quá trình tìm kiếm kết thúc.

20220317161217.png

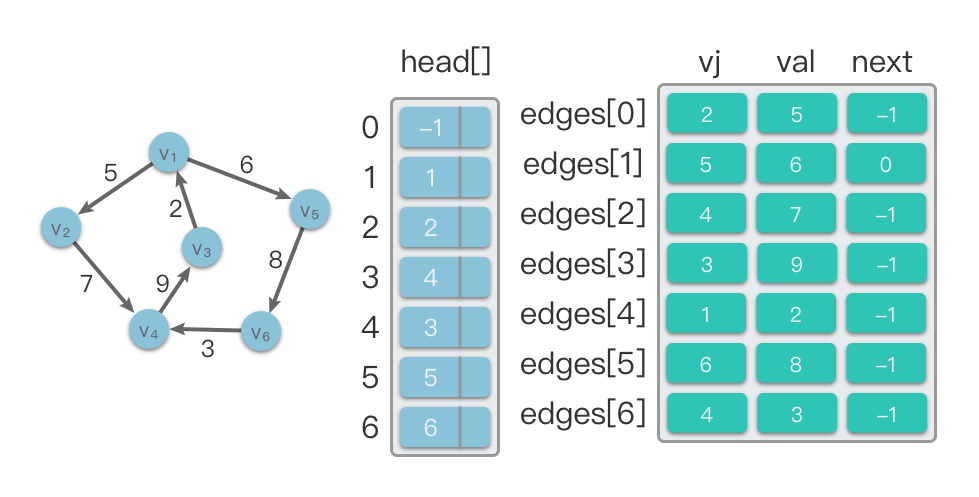
1.4.2 Phân tích thuật toán của chuỗi liên kết đỉnh đầu

Độ phức tạp thời gian của chuỗi liên kết đỉnh đầu:

• Hoạt động khởi tạo và tạo đồ thị: $O(n + m)$.
• Kiểm tra xem có cạnh từ $v_i$ đến $v_j$ hay không: $O(TD(v_i))$.
• Duyệt qua tất cả các cạnh của một đỉnh: $O(TD(v_i))$.
• Duyệt qua toàn bộ đồ thị: $O(n + m)$.

Độ phức tạp không gian của chuỗi liên kết đỉnh đầu:

• Độ phức tạp không gian: $O(n + m)$.

1.4.3 Cài đặt mã của chuỗi liên kết đỉnh đầu

class EdgeNode:                                 # Lớp thông tin cạnh
    def __init__(self, vj, val):
        self.vj = vj                            # Đỉnh kết thúc của cạnh
        self.val = val                          # Trọng số của cạnh
        self.next = None                        # Cạnh tiếp theo
        
class Graph:
    def __init__(self, ver_count, edge_count):
        self.ver_count = ver_count              # Số đỉnh
        self.edge_count = edge_count            # Số cạnh
        self.head = [-1 for _ in range(ver_count)]  # Mảng đầu đỉnh
        self.edges = []                         # Mảng cạnh
    
    # Kiểm tra đỉnh v có hợp lệ hay không
    def __valid(self, v):
        return 0 <= v <= self.ver_count
    
    # Hoạt động tạo đồ thị, edges là thông tin cạnh
    def creatGraph(self, edges=[]):
        for i in range(len(edges)):
            vi, vj, val = edges[i]
            self.add_edge(i, vi, vj, val)
            
    # Thêm cạnh vi - vj vào mảng cạnh của đồ thị
    def add_edge(self, index, vi, vj, val):
        if not self.__valid(vi) or not self.__valid(vj):
            raise ValueError(str(vi) + ' hoặc ' + str(vj) + " không phải là đỉnh hợp lệ.")
            
        edge = EdgeNode(vj, val)                # Tạo đối tượng cạnh
        edge.next = self.head[vi]               # Cạnh tiếp theo trỏ đến con trỏ đầu cũ
        self.edges.append(edge)                 # Thêm cạnh vào mảng cạnh
        self.head[vi] = index                   # Con trỏ đầu trỏ tới chỉ số của cạnh mới trong mảng cạnh
    
    # Lấy trọng số của cạnh vi - vj
    def get_edge(self, vi, vj):
        if not self.__valid(vi) or not self.__valid(vj):
            raise ValueError(str(vi) + ' hoặc ' + str(vj) + " không phải là đỉnh hợp lệ.")
            
        index = self.head[vi]                   # Lấy chỉ số của cạnh đầu tiên kết nối với đỉnh vi trong mảng cạnh
        while index != -1:                      # index == -1 nghĩa là đã duyệt qua tất cả các cạnh kết nối với đỉnh vi
            if vj == self.edges[index].vj:      # Tìm thấy cạnh vi - vj
                return self.edges[index].val    # Trả về trọng số của cạnh vi - vj
            index = self.edges[index].next      # Lấy chỉ số của cạnh tiếp theo kết nối với đỉnh vi trong mảng cạnh
        return None                             # Không tìm thấy cạnh vi - vj
    
    # In các cạnh của đồ thị dựa trên chuỗi liên kết đỉnh đầu
    def printGraph(self):
        for vi in range(self.ver_count):        # Duyệt qua tất cả các đỉnh vi
            index = self.head[vi]               # Lấy chỉ số của cạnh đầu tiên kết nối với đỉnh vi trong mảng cạnh
            while index != -1:                  # index == -1 nghĩa là đã duyệt qua tất cả các cạnh kết nối với đỉnh vi
                print(str(vi) + ' - ' + str(self.edges[index].vj) + ' : ' + str(self.edges[index].val))
                index = self.edges[index].next  # Lấy chỉ số của cạnh tiếp theo kết nối với đỉnh vi trong mảng cạnh
                

graph = Graph(7, 7)
edges = [[1, 2, 5],[1, 5, 6],[2, 4, 7],[4, 3, 9],[3, 1, 2],[5, 6, 8],[6, 4, 3]]
graph.creatGraph(edges)    
print(graph.get_edge(4, 3))
print(graph.get_edge(4, 5))
graph.printGraph()

1.5 Bảng băm thực hiện bảng kề

1.5.1 Mô tả nguyên lý của bảng băm thực hiện bảng kề

Trong Python, ta có thể dễ dàng thực hiện bảng kề bằng cách sử dụng bảng băm (từ điển). Bảng băm thực hiện bảng kề bao gồm hai bảng băm: bảng băm đầu tiên được sử dụng để lưu trữ thông tin về các đỉnh, khóa của bảng băm là các đỉnh và giá trị là một bảng băm khác chứa thông tin về các cạnh kề của đỉnh đó. Bảng băm thứ hai được sử dụng để lưu trữ thông tin về các cạnh kề của đỉnh, khóa của bảng băm này là đỉnh đích của cạnh và giá trị là trọng số của cạnh.

1.5.2 Phân tích thuật toán của bảng băm thực hiện bảng kề

Độ phức tạp thời gian của bảng băm thực hiện bảng kề:

• Hoạt động khởi tạo và tạo đồ thị: $O(n + m)$.
• Kiểm tra xem có cạnh từ $v_i$ đến $v_j$ hay không: $O(1)$.
• Duyệt qua tất cả các cạnh của một đỉnh: $O(TD(v_i))$.
• Duyệt qua toàn bộ đồ thị: $O(n + m)$.

Độ phức tạp không gian của bảng băm thực hiện bảng kề:

• Độ phức tạp không gian: $O(n + m)$.

1.5.3 Cài đặt mã của bảng băm thực hiện bảng kề

class VertexNode:                               # Lớp thông tin đỉnh
    def __init__(self, vi):
        self.vi = vi                            # Đỉnh
        self.adj_edges = dict()                 # Bảng băm chứa các cạnh kề
        
class Graph:
    def __init__(self):
        self.vertices = dict()                   # Bảng băm chứa các đỉnh
    
    # Hoạt động tạo đồ thị, edges là thông tin cạnh
    def creatGraph(self, edges=[]):
        for vi, vj, val in edges:
            self.add_edge(vi, vj, val)
    
    # Thêm đỉnh vào đồ thị
    def add_vertex(self, vi):
        vertex = VertexNode(vi)
        self.vertices[vi] = vertex
    
    # Thêm cạnh vi - vj vào bảng kề của đồ thị
    def add_edge(self, vi, vj, val):        
        if vi not in self.vertices:
            self.add_vertex(vi)
        if vj not in self.vertices:
            self.add_vertex(vj)
        
        self.vertices[vi].adj_edges[vj] = val
        
    # Lấy trọng số của cạnh vi - vj
    def get_edge(self, vi, vj):
        if vi in self.vertices and vj in self.vertices[vi].adj_edges:
            return self.vertices[vi].adj_edges[vj]
        return None
    
    # In các cạnh của đồ thị dựa trên bảng kề
    def printGraph(self):
        for vi in self.vertices:
            for vj in self.vertices[vi].adj_edges:
                print(str(vi) + ' - ' + str(vj) + ' : ' + str(self.vertices[vi].adj_edges[vj]))


graph = Graph()
edges = [[1, 2, 5],[1, 5, 6],[2, 4, 7],[4, 3, 9],[3, 1, 2],[5, 6, 8],[6, 4, 3]]
graph.creatGraph(edges)
print(graph.get_edge(3, 4))
graph.printGraph()

2. Ứng dụng của vấn đề đồ thị

Đồ thị và thuật toán đồ thị đóng vai trò quan trọng trong khoa học máy tính, cung cấp một cách mô hình hóa đơn giản và hệ thống cho nhiều vấn đề. Nhiều vấn đề thực tế có thể chuyển thành vấn đề đồ thị và được giải quyết bằng các thuật toán đồ thị. Ví dụ:

• Thiết kế và định tuyến mạch tích hợp.
• Thiết kế định tuyến mạng Internet và điện thoại di động.
• Vấn đề lập kế hoạch dự án kỹ thuật.

Các vấn đề ứng dụng của đồ thị phổ biến có thể được chia thành các loại sau: vấn đề duyệt đồ thị, vấn đề liên thông đồ thị, vấn đề cây khung của đồ thị, vấn đề đường đi ngắn nhất của đồ thị, vấn đề luồng mạng của đồ thị, vấn đề đồ thị hai phía và nhiều hơn nữa.

2.1 Vấn đề duyệt đồ thị

Duyệt đồ thị: Tương tự như duyệt cây, duyệt đồ thị là quá trình bắt đầu từ một đỉnh của đồ thị và duyệt qua tất cả các đỉnh khác trong đồ thị theo một cách tìm kiếm nhất định.

Duyệt đồ thị là cơ sở cho các thuật toán giải quyết vấn đề liên thông, sắp xếp đồ thị và tìm đường đi quan trọng.

Dựa trên cách tìm kiếm khác nhau, duyệt đồ thị có thể được chia thành "duyệt theo chiều sâu" và "duyệt theo chiều rộng".

• Duyệt theo chiều sâu: Bắt đầu từ một đỉnh, tiếp tục theo một đường đi cụ thể cho đến khi không thể đi tiếp, sau đó quay lại các đỉnh đã đi qua gần nhất.
• Duyệt theo chiều rộng: Bắt đầu từ một đỉnh, duyệt qua tất cả các đỉnh kề cạnh chưa được duyệt, sau đó duyệt qua các đỉnh kề cạnh của các đỉnh đã duyệt và tiếp tục như vậy cho đến khi duyệt qua tất cả các đỉnh.

2.2 Vấn đề liên thông đồ thị

Chúng ta đã đề cập đến "2.3 Đồ thị liên thông và đồ thị không liên thông" trong phần [[Graph Basic]].

Trong đồ thị vô hướng, vấn đề liên thông đồ thị chủ yếu bao gồm: tìm thành phần liên thông của đồ thị, tìm thành phần liên thông kép (tìm điểm cắt), tìm thành phần liên thông cạnh (tìm cầu), vấn đề cắt tối thiểu toàn cục và nhiều hơn nữa.

Trong đồ thị có hướng, vấn đề liên thông đồ thị chủ yếu bao gồm: tìm thành phần liên thông mạnh của đồ thị, cơ sở điểm nhỏ nhất, cơ sở điểm nhỏ nhất trọng số và vấn đề 2-SAT và nhiều hơn nữa.

2.3 Vấn đề cây khung của đồ thị

Cây khung của đồ thị (Spanning Tree): Nếu một đồ thị liên thông G có một đồ thị con là một cây chứa tất cả các đỉnh của đồ thị G, thì đồ thị con đó được gọi là cây khung của đồ thị G. Cây khung là một đồ thị con liên thông tối thiểu chứa tất cả các đỉnh của đồ thị.

Vấn đề cây khung của đồ thị chủ yếu bao gồm: vấn đề cây khung nhỏ nhất, vấn đề cây khung nhỏ nhất thứ hai và vấn đề cây hình của đồ thị có hướng và nhiều hơn nữa.

• Cây khung nhỏ nhất của đồ thị vô hướng: Nếu đồ thị liên thông G là một đồ thị có trọng số, các cạnh của cây khung cũng có trọng số, thì cây khung có tổng trọng số nhỏ nhất trong tất cả các cây khung được gọi là cây khung nhỏ nhất (còn được gọi là cây khung tối ưu hoặc cây khung nhỏ nhất).
• Cây khung nhỏ nhất thứ hai của đồ thị vô hướng: Nếu đồ thị liên thông G là một đồ thị có trọng số, các cạnh của cây khung cũng có trọng số, thì cây khung có tổng trọng số nhỏ nhất thứ hai trong tất cả các cây khung được gọi là cây khung nhỏ nhất thứ hai.
• Cây hình của đồ thị có hướng: Nếu đồ thị G là một đồ thị có hướng và có một cây khung có trọng số nhỏ nhất, trong đó có một đỉnh được chọn làm gốc và từ gốc có thể đi đến tất cả các đỉnh khác, thì cây khung đó được gọi là cây hình của đồ thị có hướng.

2.3 Vấn đề cây khung của đồ thị

Cây khung của đồ thị (Spanning Tree): Nếu một đồ thị liên thông G có một đồ thị con là một cây chứa tất cả các đỉnh của đồ thị G, thì đồ thị con đó được gọi là cây khung của G. Cây khung là một đồ thị con liên thông nhỏ nhất chứa tất cả các đỉnh của đồ thị. Cây khung của đồ thị không duy nhất. Bằng cách duyệt từ các đỉnh khác nhau, ta có thể thu được các cây khung khác nhau.

Vấn đề cây khung của đồ thị chủ yếu bao gồm: vấn đề cây khung nhỏ nhất, vấn đề cây khung nhỏ nhì và vấn đề cây hình của đồ thị có hướng.

• Cây khung nhỏ nhất của đồ thị vô hướng: Nếu đồ thị liên thông G là một đồ thị có trọng số, thì các cạnh của cây khung cũng có trọng số, và cây khung có tổng trọng số nhỏ nhất trong tất cả các cây khung của đồ thị được gọi là cây khung nhỏ nhất (còn được gọi là cây khung tối ưu nhỏ nhất).
• Cây khung nhỏ nhì của đồ thị vô hướng: Nếu đồ thị liên thông G là một đồ thị có trọng số, và cây khung T là một cây khung nhỏ nhất của đồ thị G, nếu có một cây khung T1 khác, T1 ≠ T, và không tồn tại một cây khung T' khác, T' ≠ T, sao cho w(T') < w(T1), thì cây khung T1 được gọi là cây khung nhỏ nhì của đồ thị G.
• Cây hình nhỏ nhất của đồ thị có hướng: Nếu đồ thị liên thông G là một đồ thị có trọng số, và cây khung T có gốc tại đỉnh vi, và từ đỉnh vi đến bất kỳ đỉnh không phải vi nào khác trong cây khung T đều tồn tại và duy nhất, và tổng trọng số của cây khung T là nhỏ nhất, thì cây khung T được gọi là cây hình nhỏ nhất của đồ thị có hướng G.

2.4 Vấn đề đường đi ngắn nhất của đồ thị

Vấn đề đường đi ngắn nhất của đồ thị: Nếu sử dụng đồ thị có trọng số để biểu diễn mạng giao thông, vận chuyển hàng hóa hoặc mạng xã hội thực tế, thì trọng số của các cạnh có thể đại diện cho phí vận chuyển, khoảng cách hoặc mức độ quen thuộc. Trong trường hợp này, chúng ta quan tâm đến độ dài của đường đi ngắn nhất giữa hai đỉnh khác nhau, và loại vấn đề này được gọi chung là vấn đề đường đi ngắn nhất. Đỉnh đầu tiên trên đường đi được gọi là điểm nguồn, và đỉnh cuối cùng được gọi là điểm đích.

Dựa vào số lượng điểm nguồn khác nhau, vấn đề đường đi ngắn nhất của đồ thị có thể được chia thành vấn đề đường đi ngắn nhất từ một nguồn và vấn đề đường đi ngắn nhất từ nhiều nguồn.

• Vấn đề đường đi ngắn nhất từ một nguồn: Vấn đề đường đi ngắn nhất từ một đỉnh xuất phát đến tất cả các đỉnh còn lại trong đồ thị.
• Vấn đề đường đi ngắn nhất từ nhiều nguồn: Vấn đề đường đi ngắn nhất giữa hai đỉnh bất kỳ trong đồ thị.

Việc giải quyết vấn đề đường đi ngắn nhất từ một nguồn là cơ sở cho việc giải quyết hệ thống ràng buộc chênh lệch.

Ngoài ra, trong ứng dụng thực tế, đôi khi ngoài việc biết đường đi ngắn nhất, còn cần biết đường đi ngắn nhì hoặc thứ ba ngắn nhất. Các vấn đề đa đường đi ngắn nhất như vậy được gọi là vấn đề k đường đi ngắn nhất.

2.5 Vấn đề luồng mạng của đồ thị

Luồng mạng của đồ thị: Ở đây, "mạng" đề cập đến đồ thị có hướng liên thông với trọng số. Mỗi cạnh trong đồ thị có một trọng số (còn được gọi là giới hạn), và khi không có cạnh nối giữa hai đỉnh, trọng số giữa hai đỉnh đó là 0. Đồ thị có hai đỉnh đặc biệt: nguồn $s$ và đích $t$.

Vấn đề chính trong luồng mạng của đồ thị là vấn đề luồng mạng tối đa. Ngoài ra, còn có các vấn đề khác như vấn đề luồng mạng tối thiểu với chi phí tối đa, vấn đề cắt mạng tối thiểu.

• Vấn đề luồng mạng tối đa: Cho một mạng, yêu cầu tính toán luồng tối đa từ nguồn đến đích (có thể có nhiều đường dẫn đến đích).
• Vấn đề luồng mạng tối thiểu với chi phí tối đa: Cho một mạng và mỗi cạnh có một chi phí, đại diện cho chi phí của mỗi đơn vị luồng qua cạnh đó. Yêu cầu tính toán luồng tối đa trong khi đồng thời chi phí là tối thiểu.
• Vấn đề cắt mạng tối thiểu: Cắt là việc xóa cạnh. Cho một mạng, loại bỏ $x$ cạnh để làm cho mạng ban đầu không còn liên thông, yêu cầu tính toán tổng luồng nhỏ nhất của $x$ cạnh đó.

2.6 Vấn đề đồ thị hai phía

Đồ thị hai phía: Cho $G = (V, E)$ là một đồ thị vô hướng, nếu tập đỉnh $V$ có thể chia thành hai tập con không giao nhau $(A, B)$ sao cho mỗi cạnh $(u, v)$ trong đồ thị có hai đỉnh $u$ và $v$ thuộc hai tập con khác nhau (tức là $u \in A, v \in B$), thì đồ thị $G$ được gọi là đồ thị hai phía.

Các vấn đề phổ biến trong đồ thị hai phía bao gồm: vấn đề ghép cặp tối đa trong đồ thị hai phía, vấn đề ghép cặp tối đa với trọng số tối đa trong đồ thị hai phía, vấn đề ghép cặp đa phương trong đồ thị hai phía.

Trước tiên, hãy tìm hiểu về khái niệm ghép cặp: Trong đồ thị hai phía, một ghép cặp là một tập hợp các cạnh, trong đó mỗi đỉnh chỉ có tối đa một cạnh kết nối với nó.

• Vấn đề ghép cặp tối đa trong đồ thị hai phía: Trong tất cả các ghép cặp có thể có trong đồ thị hai phía, tìm ghép cặp có số cạnh tối đa.
• Vấn đề ghép cặp tối đa với trọng số tối đa trong đồ thị hai phía: Trong tất cả các ghép cặp có thể có trong đồ thị hai phía, tìm ghép cặp có tổng trọng số cạnh tối đa.
• Vấn đề ghép cặp đa phương trong đồ thị hai phía: Trong đồ thị hai phía, cho trước một số lượng cạnh tối đa mà mỗi đỉnh có thể ghép, tìm ghép cặp sao cho số lượng cạnh ghép là tối đa.