Graph Basic

1. Định nghĩa đồ thị

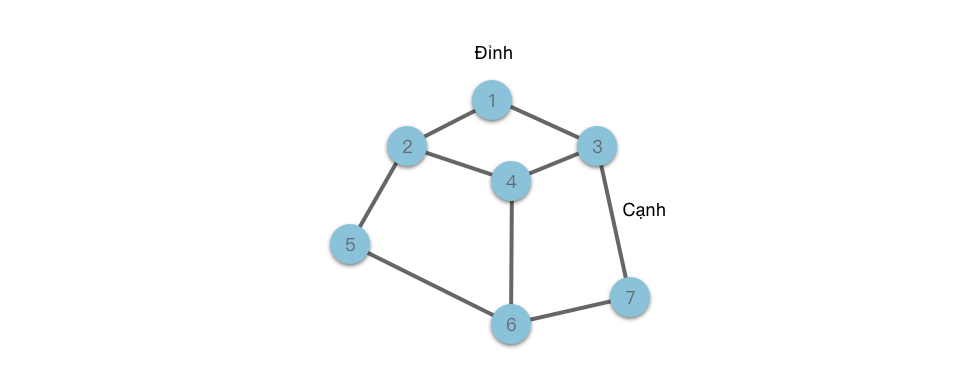
Đồ thị (Graph): là một cấu trúc được tạo thành từ tập hợp hữu hạn và không rỗng các đỉnh $V$ (gồm $n > 0$ đỉnh) và tập hợp các cạnh $E$ (mô tả mối quan hệ giữa các đỉnh). Định nghĩa hình thức của đồ thị là $G = (V, E)$ .

Đỉnh (Vertex): là các phần tử dữ liệu trong đồ thị, thường được biểu diễn bằng các hình tròn trong hình vẽ đồ thị.
Cạnh (Edge): là mối quan hệ giữa hai phần tử dữ liệu trong đồ thị, thường được biểu diễn bằng các đoạn thẳng nối hai đỉnh trong hình vẽ đồ thị. Cạnh được định nghĩa hình thức là $e = \langle u, v \rangle$ , biểu thị một cạnh từ $u$ đến $v$ , trong đó $u$ được gọi là đỉnh xuất phát, $v$ được gọi là đỉnh kết thúc.

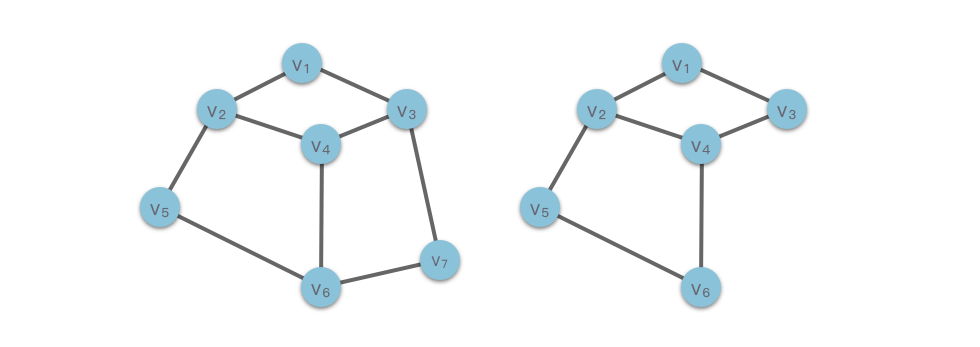
Đồ thị con (Sub Graph): Đối với đồ thị $G = (V, E)$ và $G^{'} = (V^{'}, E^{'})$ , nếu tồn tại $V^{'} \subseteq V$ , $E^{'} \subseteq E$ , thì $G^{'}$ được gọi là đồ thị con của $G$ . Đặc biệt, theo định nghĩa, $G$ cũng là đồ thị con của chính nó.

2. Phân loại đồ thị

2.1 Đồ thị vô hướng và đồ thị có hướng

Dựa trên việc các cạnh có hướng hay không, chúng ta có thể chia đồ thị thành hai loại: "đồ thị vô hướng" và "đồ thị có hướng".

Đồ thị vô hướng (Undirected Graph): Nếu mỗi cạnh trong đồ thị không có hướng, thì được gọi là đồ thị vô hướng. Ví dụ như đồ thị quan hệ bạn bè, đồ thị đường đi đều là đồ thị vô hướng.
Đồ thị có hướng (Directed Graph): Nếu mỗi cạnh trong đồ thị có hướng, thì được gọi là đồ thị có hướng. Ví dụ như đồ thị quy trình là đồ thị có hướng.

Trong đồ thị vô hướng, mỗi cạnh được biểu diễn bởi một cặp không thứ tự của hai đỉnh. Ví dụ, trong hình vẽ bên trái, cạnh giữa đỉnh $v_1$ và đỉnh $v_2$ được ký hiệu là $(v_1, v_2)$ hoặc $(v_2, v_1)$ .

Trong đồ thị có hướng, cạnh có hướng còn được gọi là cung, mỗi cung được biểu diễn bởi một cặp có thứ tự của hai đỉnh. Ví dụ, trong hình vẽ bên phải, cung từ đỉnh $v_1$ đến đỉnh $v_2$ được ký hiệu là $\langle v_1, v_2 \rangle$ , $v_1$ được gọi là đầu cung, $v_2$ được gọi là đuôi cung.

Nếu đồ thị vô hướng có $n$ đỉnh, thì số lượng cạnh tối đa trong đồ thị vô hướng là $n \times (n - 1) / 2$ . Đồ thị vô hướng có $n \times (n - 1) / 2$ cạnh được gọi là "đồ thị vô hướng hoàn chỉnh (Completed Undirected Graph)".

Nếu đồ thị có hướng có $n$ đỉnh, thì số lượng cung tối đa trong đồ thị có hướng là $n \times (n - 1)$ . Đồ thị có hướng có $n \times (n - 1)$ cung được gọi là "đồ thị có hướng hoàn chỉnh (Completed Directed Graph)".

Ví dụ hình vẽ bên dưới, bên trái là đồ thị vô hướng hoàn chỉnh với 4 đỉnh, bên phải là đồ thị có hướng hoàn chỉnh với 4 đỉnh.

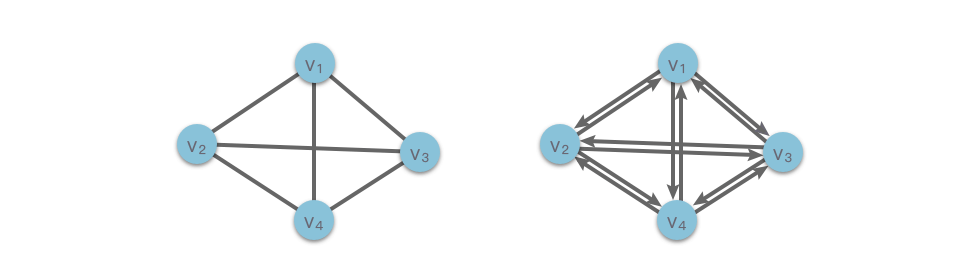
Dưới đây là giới thiệu về một khái niệm quan trọng trong đồ thị vô hướng và đồ thị có hướng, đó là "độ của đỉnh".

Độ của đỉnh: Là số lượng cạnh liên quan đến đỉnh $v_i$ , ký hiệu là $TD(v_i)$ .

Ví dụ trong đồ thị vô hướng hoàn chỉnh bên trái, đỉnh $v_3$ có độ là $3$ .

Trong đồ thị có hướng, chúng ta có thể chia độ của đỉnh thành "độ ra" và "độ vào".

Độ ra của đỉnh: Là số lượng cung xuất phát từ đỉnh $v_i$ , ký hiệu là $OD(v_i)$ .
Độ vào của đỉnh: Là số lượng cung kết thúc tại đỉnh $v_i$ , ký hiệu là $ID(v_i)$ .
Độ của đỉnh trong đồ thị có hướng = Độ ra của đỉnh + Độ vào của đỉnh, tức là $TD(v_i) = OD(v_i) + ID(v_i)$ .

Ví dụ trong đồ thị có hướng hoàn chỉnh bên phải, đỉnh $v_3$ có độ ra là $3$ , độ vào là $3$ , độ của đỉnh $v_3$ là $3 + 3 = 6$ .

2.2 Đồ thị có chu trình và đồ thị không có chu trình

"Đường đi" là một khái niệm quan trọng trong đồ thị, đối với đồ thị $G = (V, E)$ , nếu tồn tại chuỗi đỉnh $v_{i_0}, v_{i_1}, v_{i_2},… , v_{i_m}$ sao cho $(v_{i_0}, v_{i_1}), (v_{i_1}, v_{i_2}), …, (v_{i_{m-1}}, v_{i_m}) \in E$ (đối với đồ thị có hướng thì là $\langle v_{i_0}, v_{i_1} \rangle, \langle v_{i_1}, v_{i_2} \rangle, …, \langle v_{i_{m-1}}, v_{i_m} \rangle \in E$ ), thì chuỗi đỉnh đó được gọi là một đường đi từ đỉnh $v_{i_0}$ đến đỉnh $v_{i_m}$ , trong đó $v_{i_0}$ là điểm bắt đầu của đường đi và $v_{i_m}$ là điểm kết thúc của đường đi.

Nói một cách đơn giản, nếu có thể đi từ đỉnh $v_{i_0}$ đến đỉnh $v_{i_m}$ thông qua một chuỗi các đỉnh và cạnh, thì có một đường đi từ $v_{i_0}$ đến $v_{i_m}$ , và chuỗi các đỉnh đi qua được gọi là đường đi giữa hai đỉnh.

Chu trình (Cycle): Nếu đường đi có điểm bắt đầu và điểm kết thúc giống nhau (tức là $v_{i_0} == v_{i_m}$ ), thì đường đi đó được gọi là "chu trình" hoặc "vòng".
Đường đi đơn (Simple Path): Đường đi mà không có đỉnh lặp lại trong chuỗi đỉnh được gọi là "đường đi đơn".

Dựa trên sự có hay không có chu trình trong đồ thị, chúng ta có thể chia đồ thị thành "đồ thị có chu trình" và "đồ thị không có chu trình".

Đồ thị có chu trình (Cyclic Graph): Nếu đồ thị có ít nhất một chu trình, thì đồ thị đó được gọi là "đồ thị có chu trình".
Đồ thị không có chu trình (Acyclic Graph): Nếu đồ thị không có chu trình, thì đồ thị đó được gọi là "đồ thị không có chu trình".

Đặc biệt, trong đồ thị có hướng, nếu không có chu trình, thì đồ thị đó được gọi là "đồ thị có hướng không chu trình (Directed Acyclic Graph)", viết tắt là DAG. Vì đồ thị có hướng không chu trình có cấu trúc đặc biệt, nó thường được sử dụng trong việc xử lý động, tìm đường đi ngắn nhất trong định hướng, nén dữ liệu và nhiều thuật toán khác.

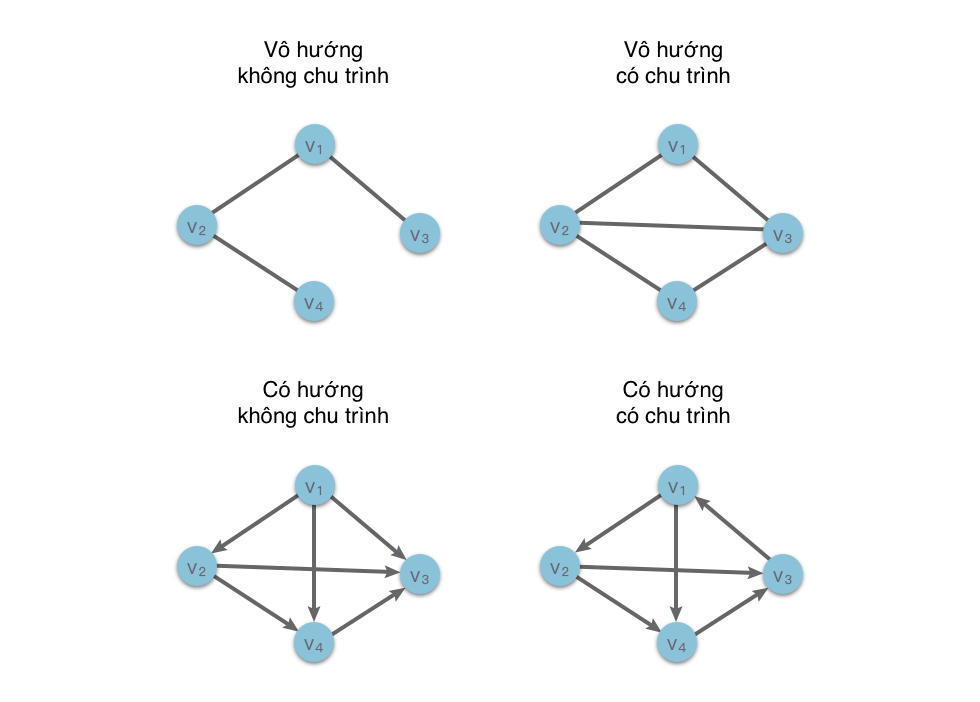
Ví dụ hình vẽ dưới đây, lần lượt là: đồ thị vô hướng không chu trình, đồ thị vô hướng có chu trình, đồ thị có hướng không chu trình và đồ thị có hướng có chu trình. Trong đồ thị có hướng có chu trình, các đỉnh $v_1$ , $v_2$ , $v_3$ và các cạnh kết nối chúng tạo thành một chu trình.

2.3 Đồ thị liên thông và đồ thị không liên thông

2.3.1 Đồ thị vô hướng liên thông và thành phần liên thông

Trong đồ thị vô hướng, nếu có một đường đi từ đỉnh $v_i$ đến đỉnh $v_j$ , thì ta nói đỉnh $v_i$ và $v_j$ là liên thông.

Đồ thị vô hướng liên thông: Trong đồ thị vô hướng, nếu mọi cặp đỉnh trong đồ thị đều liên thông với nhau, thì đồ thị đó được gọi là đồ thị vô hướng liên thông.
Đồ thị vô hướng không liên thông: Trong đồ thị vô hướng, nếu có ít nhất một cặp đỉnh mà không có đường đi nào giữa chúng, thì đồ thị đó được gọi là đồ thị vô hướng không liên thông.

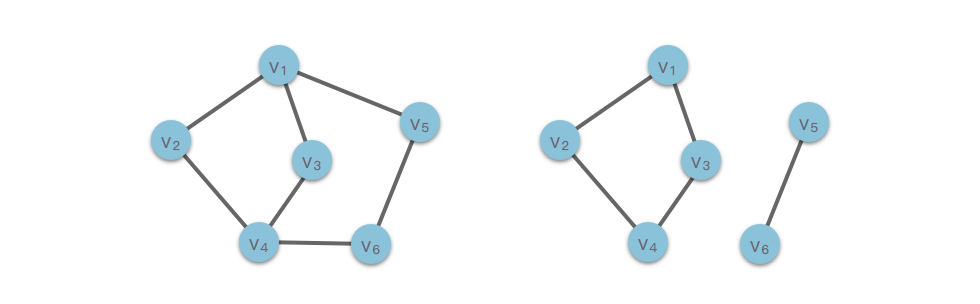
Ví dụ trong hình vẽ dưới đây, đồ thị vô hướng bên trái có tất cả các đỉnh đều liên thông với nhau, nên đó là một đồ thị vô hướng liên thông. Đồ thị vô hướng bên phải có đỉnh $v_1$ liên thông với $v_2$ , $v_3$ và $v_4$ , nhưng không có đường đi từ $v_1$ đến $v_5$ , nên đó là một đồ thị vô hướng không liên thông.

Dưới đây là khái niệm về "thành phần liên thông" trong đồ thị vô hướng. Một số đồ thị vô hướng có thể không liên thông, nhưng các đồ thị con của chúng có thể là liên thông. Các đồ thị con này được gọi là thành phần liên thông của đồ thị gốc. Một thành phần liên thông cực đại (không tồn tại thành phần liên thông lớn hơn nó) được gọi là thành phần liên thông của đồ thị.

Thành phần liên thông: Nếu một đồ thị con của đồ thị vô hướng là một đồ thị vô hướng liên thông, thì đồ thị con đó được gọi là thành phần liên thông của đồ thị gốc.
Thành phần liên thông cực đại: Một thành phần liên thông của đồ thị vô hướng mà không có thành phần liên thông lớn hơn nó được gọi là thành phần liên thông cực đại.

Ví dụ trong hình vẽ dưới đây, đồ thị vô hướng không liên thông bên phải có hai thành phần liên thông: thành phần liên thông gồm các đỉnh $v_1$ , $v_2$ , $v_3$ , $v_4$ và thành phần liên thông gồm các đỉnh $v_5$ , $v_6$ . Cả hai thành phần liên thông này đều là thành phần liên thông cực đại của đồ thị.

2.3.2 Đồ thị có hướng liên thông mạnh và thành phần liên thông mạnh

Trong đồ thị có hướng, nếu có một đường đi từ đỉnh $v_i$ đến $v_j$ và từ $v_j$ đến $v_i$ , thì ta nói đỉnh $v_i$ và $v_j$ là liên thông.

Đồ thị có hướng liên thông mạnh: Trong đồ thị có hướng, nếu mọi cặp đỉnh $v_i$ và $v_j$ , từ $v_i$ đến $v_j$ và từ $v_j$ đến $v_i$ đều có đường đi, thì đồ thị đó được gọi là đồ thị có hướng liên thông mạnh.
Đồ thị có hướng không liên thông mạnh: Trong đồ thị có hướng, nếu có ít nhất một cặp đỉnh mà không có đường đi từ $v_i$ đến $v_j$ và từ $v_j$ đến $v_i$ , thì đồ thị đó được gọi là đồ thị có hướng không liên thông mạnh.

Ví dụ trong hình vẽ dưới đây, đồ thị có hướng liên thông mạnh bên trái có đường đi từ mọi cặp đỉnh. Đồ thị có hướng không liên thông mạnh bên phải có đỉnh $v_7$ không có đường đi đến bất kỳ đỉnh nào khác, nên đó là một đồ thị có hướng không liên thông mạnh.

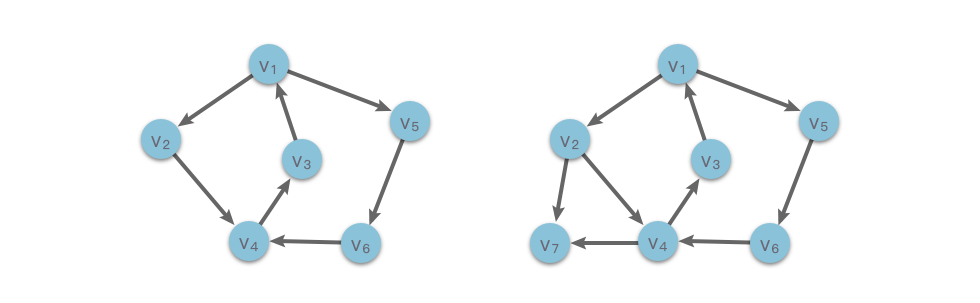
Tương tự như đồ thị vô hướng, đồ thị có hướng cũng có khái niệm về "thành phần liên thông mạnh". Một số đồ thị có hướng có thể không liên thông mạnh, nhưng các đồ thị con của chúng có thể là liên thông mạnh. Các đồ thị con này được gọi là thành phần liên thông mạnh của đồ thị gốc. Một thành phần liên thông mạnh cực đại (không tồn tại thành phần liên thông mạnh lớn hơn nó) được gọi là thành phần liên thông mạnh của đồ thị.

Thành phần liên thông mạnh: Nếu một đồ thị con của đồ thị có hướng là một đồ thị có hướng liên thông mạnh, thì đồ thị con đó được gọi là thành phần liên thông mạnh của đồ thị gốc.
Thành phần liên thông mạnh cực đại: Một thành phần liên thông mạnh của đồ thị có hướng mà không có thành phần liên thông mạnh lớn hơn nó được gọi là thành phần liên thông mạnh cực đại.

2.4 Đồ thị có trọng số

Đôi khi, đồ thị không chỉ cần biểu thị mối quan hệ giữa các đỉnh mà còn cần biểu thị thông tin cụ thể về mối quan hệ đó. Khi đó, chúng ta cần gán một số thông tin lên các cạnh, thông tin này được gọi là trọng số. Trong các ứng dụng cụ thể, trọng số có thể có ý nghĩa cụ thể, ví dụ như trọng số có thể đại diện cho khoảng cách, thời gian hoặc giá cả.

Đồ thị có trọng số: Nếu mỗi cạnh trong đồ thị được gán một trọng số, thì đồ thị đó được gọi là đồ thị có trọng số.
Mạng lưới: Đồ thị vô hướng có trọng số được gọi là mạng lưới.

Trong hình ví dụ dưới đây, chúng ta có một đồ thị có trọng số.

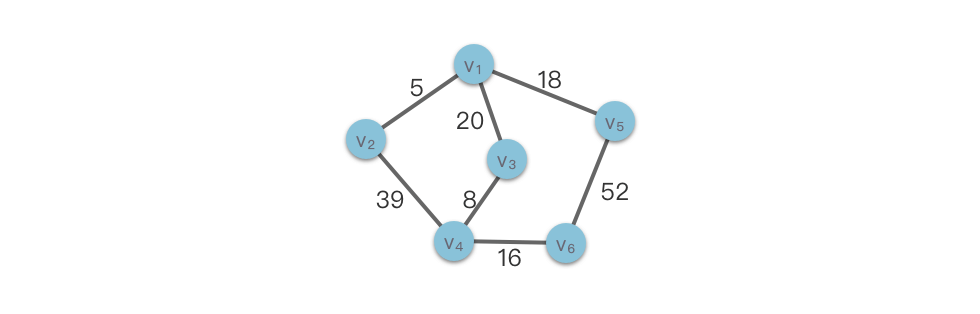
2.5 Đồ thị dày và đồ thị thưa

Dựa trên mức độ thưa của các cạnh trong đồ thị, chúng ta có thể chia đồ thị thành "đồ thị dày" và "đồ thị thưa". Đây là một khái niệm mờ nhạt và chưa có định nghĩa cụ thể.

Đồ thị dày (Dense Graph): Đồ thị có nhiều cạnh hoặc cung (số cạnh $e$ gần bằng số cạnh của đồ thị hoàn chỉnh) được gọi là đồ thị dày.
Đồ thị thưa (Sparse Graph): Đồ thị có ít cạnh hoặc cung (số cạnh $e$ nhỏ hơn rất nhiều so với số cạnh của đồ thị hoàn chỉnh, ví dụ $e < n \times \log_2n$ ) được gọi là đồ thị thưa.