Priority Queue

Giải thích chi tiết về Hàng đợi Ưu tiên PriorityQueue

Tham khảo thêm hướng dẫn về priority queue trong phần Data Structure: Priority Queue

PriorityQueue là một cấu trúc dữ liệu hàng đợi ưu tiên trong Java, được cài đặt dựa trên heap ưu tiên. Nó có thể thực hiện các thao tác chèn và xóa phần tử với độ phức tạp O(log n), và tự động duy trì thứ tự ưu tiên của các phần tử trong hàng đợi.

Đơn giản để hiểu, PriorityQueue tương tự như một hàng đợi, nhưng không phải theo cơ chế vào trước ra trước (FIFO) mà sắp xếp các phần tử theo độ ưu tiên của chúng. Khi bạn chèn một phần tử vào PriorityQueue, nó sẽ tự động đặt phần tử vào vị trí phù hợp dựa trên độ ưu tiên của nó. Khi bạn xóa một phần tử từ PriorityQueue, nó sẽ tự động lấy ra phần tử có độ ưu tiên cao nhất.

Dưới đây là một ví dụ đơn giản về PriorityQueue:

// Tạo đối tượng PriorityQueue
PriorityQueue<String> priorityQueue = new PriorityQueue<>();

// Thêm các phần tử vào PriorityQueue
priorityQueue.offer("a");
priorityQueue.offer("b");
priorityQueue.offer("c");

// In ra các phần tử trong PriorityQueue
System.out.println("Các phần tử trong PriorityQueue:");
while (!priorityQueue.isEmpty()) {
    System.out.print(priorityQueue.poll() + " ");
}

Trong đoạn mã trên, chúng ta đầu tiên tạo một đối tượng PriorityQueue và thêm ba phần tử vào đó. Sau đó, chúng ta sử dụng vòng lặp while để duyệt qua và in ra các phần tử trong PriorityQueue. Kết quả in ra như sau:

Các phần tử trong PriorityQueue:
c a b

Tiếp theo, hãy xem một ví dụ khác:

// Tạo đối tượng PriorityQueue và chỉ định thứ tự ưu tiên
PriorityQueue<String> priorityQueue = new PriorityQueue<>(Comparator.reverseOrder());

// Thêm các phần tử vào PriorityQueue
priorityQueue.offer("a");
priorityQueue.offer("b");
priorityQueue.offer("c");

// In ra các phần tử trong PriorityQueue
System.out.println("Các phần tử trong PriorityQueue:");
while (!priorityQueue.isEmpty()) {
    System.out.print(priorityQueue.poll() + " ");
}

Trong đoạn mã này, chúng ta sử dụng Comparator.reverseOrder() để chỉ định thứ tự ưu tiên của PriorityQueue là giảm dần. Điều này có nghĩa là các phần tử trong PriorityQueue sẽ được sắp xếp theo thứ tự từ lớn đến nhỏ.

Các phần còn lại của mã sẽ tương tự như ví dụ trước, hãy xem kết quả in ra:

Các phần tử trong PriorityQueue:
b a c

So sánh kết quả in ra của hai ví dụ trên, ta dễ dàng nhận thấy thứ tự hiển thị đúng ngược lại nhau.

Ứng dụng của PriorityQueue

PriorityQueue có vai trò chính là duy trì sắp xếp một tập hợp dữ liệu sao cho khi lấy dữ liệu ra, chúng có thể được thực hiện theo một thứ tự ưu tiên nhất định. Khi chúng ta gọi phương thức poll(), nó sẽ loại bỏ phần tử có ưu tiên cao nhất từ đầu hàng đợi. PriorityQueue được áp dụng rộng rãi trong nhiều tình huống như lập lịch công việc, xử lý sự kiện và các thuật toán cần sắp xếp dữ liệu.

Trong thực tế, PriorityQueue thường được sử dụng để thực hiện các thuật toán như Dijkstra, Prim, Huffman và các thuật toán khác. Dijkstra là thuật toán tính đường đi ngắn nhất trong đồ thị có trọng số. Thuật toán này sử dụng chiến lược tham lam, lần lượt chọn đỉnh gần nguồn có khoảng cách ngắn nhất và mở rộng từ đó để cập nhật giá trị khoảng cách của các đỉnh khác. Sau nhiều lần mở rộng, ta có thể thu được đường đi ngắn nhất từ nguồn đến tất cả các đỉnh khác.

Prim là thuật toán để tìm cây khung nhỏ nhất trong đồ thị liên thông có trọng số. Thuật toán này bắt đầu từ bất kỳ đỉnh nào và mở rộng dần cây khung bằng cách chọn một đỉnh gần nhất với cây khung hiện có để thêm vào.

Huffman là thuật toán nén dựa trên cây Huffman, được sử dụng để chuyển đổi một chuỗi thành mã nhị phân để nén dữ liệu. Ý tưởng chính của thuật toán là xây dựng cây Huffman sao cho các ký tự có tần suất xuất hiện cao được biểu diễn bằng mã ngắn hơn, trong khi các ký tự ít xuất hiện được biểu diễn bằng mã dài hơn, từ đó giảm kích thước dữ liệu.

Bởi vì PriorityQueue dựa trên heap để triển khai, vì vậy khi xử lý dữ liệu lớn, nó cung cấp độ phức tạp thời gian tốt hơn.

Ở đây liên quan đến việc so sánh kích thước, thứ tự tự nhiên của các phần tử có thể được đánh giá bằng cách so sánh trực tiếp với nhau (natural ordering) hoặc bằng cách truyền Comparator khi xây dựng PriorityQueue hoặc bằng cách mà phần tử có thể thực hiện Comparable interface để quyết định.

Trong PriorityQueue, mỗi phần tử đều có một ưu tiên, ưu tiên này quyết định vị trí của phần tử trong hàng đợi. Bên trong hàng đợi được duy trì bằng cách sử dụng heap nhỏ (hoặc có thể là heap lớn) để quản lý mối quan hệ ưu tiên của các phần tử. Cụ thể, heap nhỏ là một cây nhị phân hoàn chỉnh, mà mọi nút không phải lá đều có giá trị không lớn hơn giá trị của các nút con trái và phải của nó, điều này đảm bảo rằng phần tử ở đỉnh của hàng đợi (đỉnh của heap) luôn là phần tử có ưu tiên cao nhất.

Cây nhị phân hoàn chỉnh (Complete Binary Tree) là một loại cây nhị phân, trong đó trừ lớp cuối cùng, số lượng nút trong các lớp khác đều là đầy, các nút trong lớp cuối cùng luôn được căn chỉnh bên trái. Dưới đây là một ví dụ về một cây nhị phân hoàn chỉnh:

Heap là một loại cây nhị phân hoàn chỉnh, đặc điểm của heap là giá trị của nút gốc là nhỏ nhất (heap nhỏ) hoặc lớn nhất (heap lớn), và bất kỳ nút không phải gốc nào i cũng không lớn hơn (hoặc không nhỏ hơn) giá trị của nút cha của nó.

Đây là một ví dụ về một heap nhỏ chứa các số nguyên 1, 2, 3, 4, 5, 6, 7:

Đây là một ví dụ về một heap lớn:

            8
          /   \
         7     5
        / \   / \
       6   4 2   1

Do cấu trúc của cây nhị phân hoàn chỉnh khá rõ ràng, nên có thể sử dụng mảng để lưu trữ các phần tử của heap mà không cần sử dụng các con trỏ hay không gian bộ nhớ phụ thêm.

Trong heap, chỉ số của mỗi nút tương ứng với chỉ số của nó trong mảng, giả sử chỉ số của nút là i, thì chỉ số của nút cha là i/2, chỉ số của nút con trái là 2i, và chỉ số của nút con phải là 2i+1.

Giả sử có một mảng arr=[10, 20, 15, 30, 40], bây giờ chúng ta muốn chuyển nó thành một heap nhỏ.

Đầu tiên, chúng ta sắp xếp mảng theo hình thức của cây nhị phân hoàn chỉnh, như trong hình dưới đây:

Đánh số từ trên xuống dưới, từ trái sang phải, như sau:

Tiếp theo, chúng ta sẽ xác định vị trí của từng nút trong mảng theo các công thức đã đề cập. Ví dụ, chỉ số cha của nút 1 là 1/2=0, chỉ số con trái là 2*1=2, chỉ số con phải là 2*1+1=3, vì vậy nút 1 nằm ở vị trí 0 trong mảng, nút 2 nằm ở vị trí 2 trong mảng, nút 3 nằm ở vị trí 3 trong mảng.

Mảng tương ứng là [10, 20, 15, 30, 40], phù hợp với định nghĩa của heap nhỏ, tức là mỗi nút đều nhỏ hơn hoặc bằng các nút con của nó.

Được rồi, chúng ta

vẽ lại để hiểu rõ hơn.

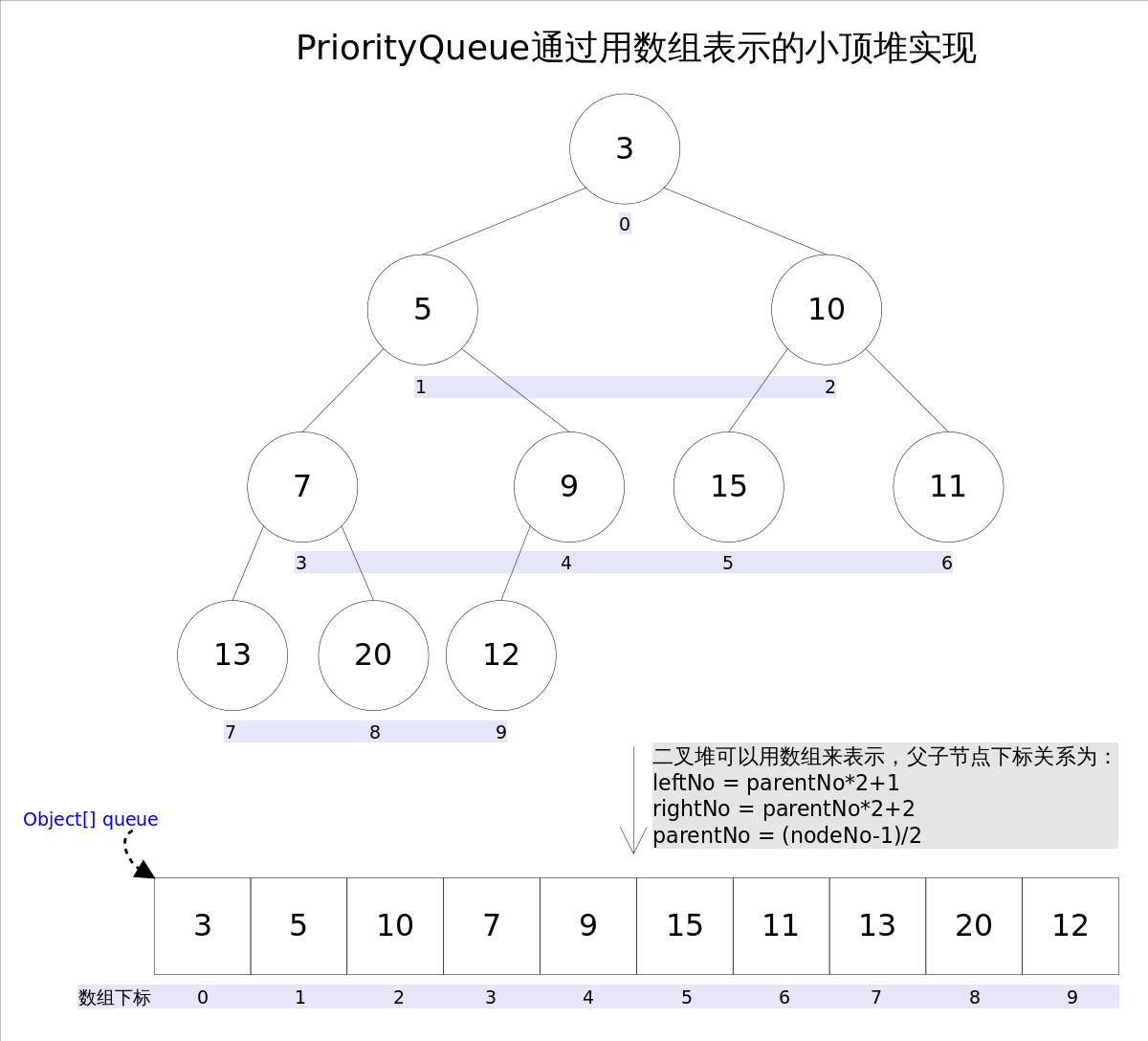
Trong hình ảnh trên, chúng tôi đã đánh số từng phần tử theo thứ tự duyệt theo tầng, nếu bạn quan sát kỹ, bạn sẽ thấy có mối liên hệ giữa nút cha và các nút con, chính xác hơn là có mối quan hệ giữa nút cha và con với các công thức sau:

leftNo = parentNo\*2+1

rightNo = parentNo\*2+2

parentNo = (nodeNo-1)/2

Sử dụng ba công thức trên, chúng ta có thể dễ dàng tính toán chỉ số cha của một nút cũng như chỉ số của nút con. Điều này cũng là lý do tại sao chúng ta có thể sử dụng mảng để lưu trữ heap.

Phân tích phương thức

Phương thức `add()` và `offer()`

add(E e) và offer(E e) có ý nghĩa giống nhau trong PriorityQueue, đều được sử dụng để chèn một phần tử vào hàng đợi ưu tiên. Sự khác biệt chính giữa chúng là cách xử lý khi thêm phần tử vào hàng đợi đã đầy: theo interface Queue, add() sẽ ném ra một ngoại lệ khi không thể chèn được phần tử, trong khi offer() sẽ trả về false.

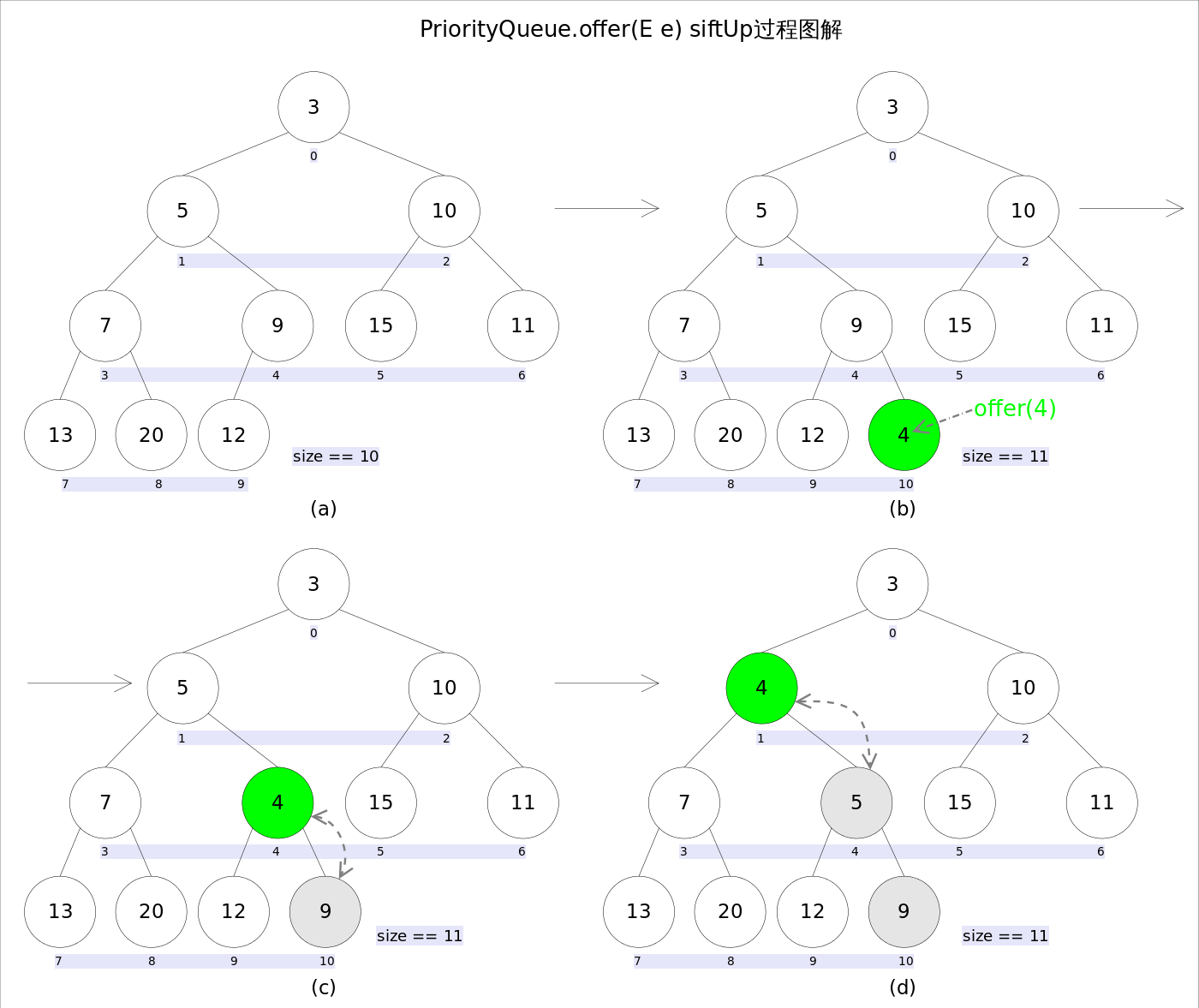
Khi một phần tử mới được thêm vào, có thể làm hỏng tính chất của heap nhỏ, vì vậy cần phải điều chỉnh cần thiết.

// Phương thức offer(E e)
public boolean offer(E e) {
    if (e == null) // Không cho phép chèn phần tử null
        throw new NullPointerException();
    modCount++;
    int i = size;
    if (i >= queue.length)
        grow(i + 1); // Tự động mở rộng
    size = i + 1;
    if (i == 0) // Nếu hàng đợi ban đầu trống, đây là phần tử đầu tiên được chèn vào
        queue[0] = e;
    else
        siftUp(i, e); // Điều chỉnh
    return true;
}

Trong đoạn mã trên, hàm mở rộng grow() tương tự như hàm grow() trong ArrayList, nghĩa là yêu cầu một mảng lớn hơn và sao chép các phần tử của mảng gốc qua. Tuy nhiên, điều quan trọng cần lưu ý là phương thức siftUp(int k, E x), hàm này được sử dụng để chèn phần tử x và duy trì tính chất của heap.

// Phương thức siftUp()
private void siftUp(int k, E x) {
    while (k > 0) {
        int parent = (k - 1) >>> 1; // parentNo = (nodeNo-1)/2
        Object e = queue[parent];
        if (comparator.compare(x, (E) e) >= 0) // Sử dụng phương thức so sánh của bộ so sánh
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = x;
}

Quá trình điều chỉnh là: Bắt đầu từ vị trí chỉ định k, so sánh và trao đổi x theo từng cấp với parent hiện tại cho đến khi thoả mãn điều kiện x >= queue[parent]. Chú ý rằng so sánh này có thể là theo thứ tự tự nhiên của các phần tử hoặc sử dụng bộ so sánh đã được cấu hình.

Phương thức `element()` và `peek()`

element() và peek() có ý nghĩa hoàn toàn giống nhau trong PriorityQueue, đều được sử dụng để lấy phần tử đầu tiên của hàng đợi mà không xóa nó đi. Sự khác biệt duy nhất giữa chúng là khi không có phần tử trong hàng đợi, element() sẽ ném ra một ngoại lệ, trong khi peek() sẽ trả về null. Theo tính chất của heap nhỏ, phần tử ở đỉnh heap là phần tử nhỏ nhất trong toàn bộ heap; vì heap được biểu diễn dưới dạng mảng, phần tử tại chỉ số 0 là phần tử ở đỉnh heap.

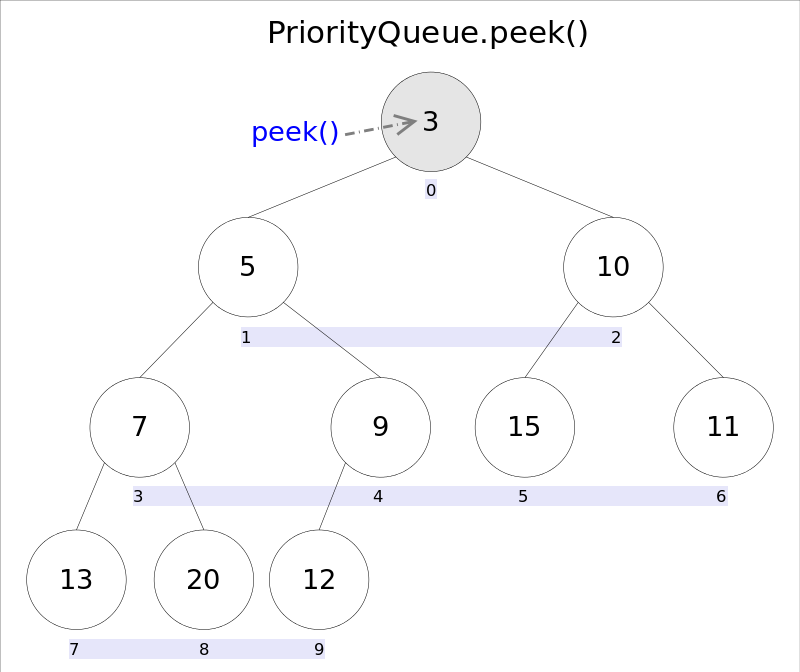
Đoạn mã rất đơn giản:

// Phương thức peek()
public E peek() {
    if (size == 0)
        return null;
    return (E) queue[0]; // Phần tử tại chỉ số 0 là phần tử nhỏ nhất
}

Phương thức `remove()` và `poll()`

remove() và poll() có ý nghĩa hoàn toàn giống nhau, đều được sử dụng để lấy và xóa phần tử đầu tiên của hàng đợi. Sự khác biệt duy nhất giữa chúng là khi không có phần tử trong hàng đợi, remove() sẽ ném ra một ngoại lệ, trong khi poll() sẽ trả về null. Do thao tác xóa có thể làm thay đổi cấu trúc của hàng đợi, để duy trì tính chất của heap nhỏ, cần phải thực hiện điều chỉnh cần thiết.

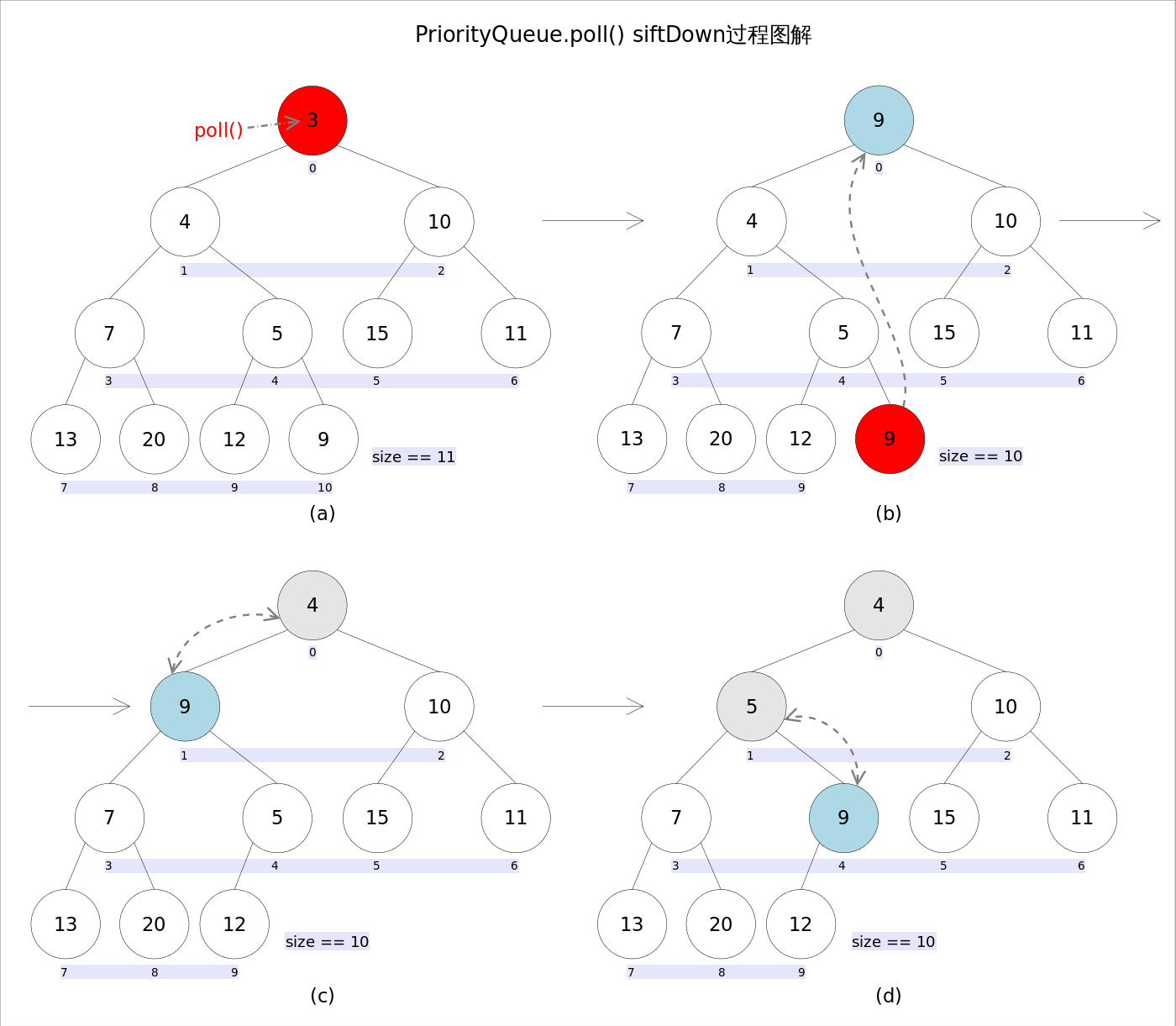
Đoạn mã như sau:

public E poll() {
    if (size == 0)
        return null;
    int s = --size;
    modCount++;
    E result = (E) queue[0]; // Phần tử tại chỉ số 0 là phần tử nhỏ nhất
    E x = (E) queue[s];
    queue[s] = null;
    if (s != 0)
        siftDown(0, x); // Điều chỉnh
    return result;
}

Trong đoạn mã trên, đầu tiên lưu lại phần tử tại chỉ số 0, sau đó thay thế phần tử này bằng phần tử cuối cùng trong mảng, và gọi hàm siftDown() để điều chỉnh heap. Hàm siftDown(int k, E x) được sử dụng để từ vị trí k chỉ định, so sánh và trao đổi x với nút con trái và phải của nút hiện tại, cho đến khi x nhỏ hơn hoặc bằng bất kỳ nút con nào.

// Phương thức siftDown()
private void siftDown(int k, E x) {
    int half = size >>> 1;
    while (k < half) {
        int child = (k << 1) + 1; // leftNo = parentNo*2+1
        Object c = queue[child];
        int right = child + 1;
        if (right < size &&
            comparator.compare((E) c, (E) queue[right]) > 0)
            c = queue[child = right];
        if (comparator.compare(x, (E) c) <= 0)
            break;
        queue[k] = c; // Thay thế nút hiện tại bằng nút con nhỏ hơn
        k = child;
    }
    queue[k] = x;
}

Phương thức `remove(Object o)`

Phương thức remove(Object o) được sử dụng để xóa một phần tử trong hàng đợi có giá trị bằng với o (nếu có nhiều phần tử bằng nhau, chỉ xóa một phần tử đầu tiên tìm thấy). Phương thức này không phải là một phương thức của interface Queue, mà là của interface Collection. Do thao tác xóa có thể làm thay đổi cấu trúc của hàng đợi, nên cần phải thực hiện điều chỉnh thích hợp.

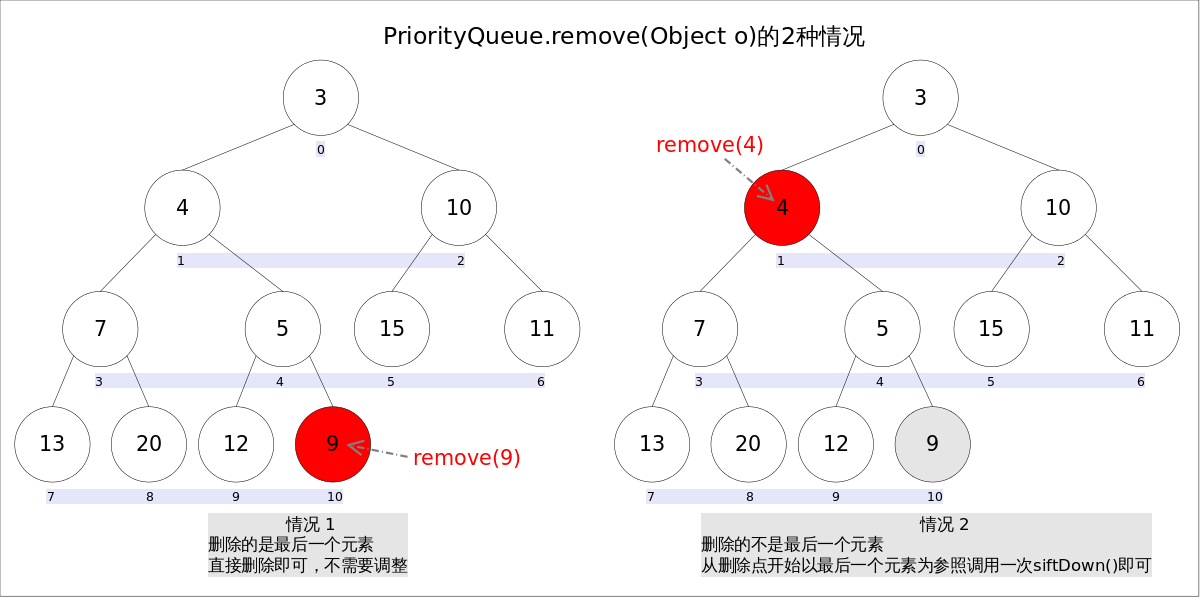
Phương thức remove(Object o) có hai trường hợp cụ thể:

Xóa phần tử cuối cùng trong hàng đợi. Trong trường hợp này, chỉ cần xóa và không cần điều chỉnh.
Xóa phần tử không phải là phần tử cuối cùng. Trong trường hợp này, từ vị trí i đã xác định, thực hiện điều chỉnh bằng cách gọi hàm siftDown() với phần tử cuối cùng trong hàng đợi.

Đoạn mã cụ thể như sau:

// Phương thức remove(Object o)
public boolean remove(Object o) {
    int i = indexOf(o); // Tìm vị trí của phần tử cần xóa
    if (i == -1)
        return false; // Nếu không tìm thấy phần tử, trả về false

    int s = --size; // Giảm kích thước của hàng đợi và lấy chỉ số của phần tử cuối cùng
    if (s == i) { // Trường hợp 1: Xóa phần tử cuối cùng
        queue[i] = null; // Đánh dấu phần tử cuối cùng là null
    } else { // Trường hợp 2: Xóa phần tử không phải cuối cùng
        E moved = (E) queue[s]; // Lấy phần tử cuối cùng
        queue[s] = null; // Đánh dấu phần tử cuối cùng là null
        siftDown(i, moved); // Điều chỉnh hàng đợi từ vị trí i với phần tử cuối cùng
        // Các bước điều chỉnh khác có thể được thực hiện ở đây nếu cần
        // ...
    }
    return true; // Trả về true khi xóa thành công
}

Trong đoạn mã trên, indexOf(o) được sử dụng để tìm chỉ số của phần tử cần xóa trong mảng queue. Nếu không tìm thấy phần tử, phương thức sẽ trả về false. Nếu tìm thấy, phương thức sẽ giảm kích thước của hàng đợi và xử lý phần tử ở vị trí tìm thấy hoặc phần tử cuối cùng của hàng đợi, sau đó gọi siftDown() để điều chỉnh lại hàng đợi.

Tổng kết

PriorityQueue là một cấu trúc dữ liệu rất phổ biến, là một triển khai đặc biệt của Heap, cho phép duy trì một tập hợp được sắp xếp một cách hiệu quả.

Được triển khai dưới dạng một mảng, sử dụng các tính chất của Heap để duy trì thứ tự của các phần tử.
Khi lấy phần tử, thực hiện theo thứ tự ưu tiên (từ thấp đến cao hoặc từ cao đến thấp).
Để chỉ định thứ tự sắp xếp, các phần tử cần phải triển khai interface Comparable hoặc truyền vào một Comparator để so sánh.