Java HashMap

Tìm hiểu chi tiết về HashMap trong Java (kèm mã nguồn)

Trong bài viết này, chúng ta sẽ đi sâu vào tìm hiểu về HashMap trong Java, bao gồm nguyên lý phương pháp băm, cơ chế mở rộng của HashMap, tại sao hệ số tải của HashMap là 0.75 mà không phải là 0.6 hoặc 0.8, và tại sao HashMap không an toàn đối với luồng, tóm lại, hầu hết các câu hỏi phỏng vấn về HashMap sẽ được giải thích trong bài viết này.

HashMap là một trong những cấu trúc dữ liệu phổ biến trong Java, được sử dụng để lưu trữ các cặp khóa-giá trị. Trong HashMap, mỗi khóa được ánh xạ đến một giá trị duy nhất, cho phép truy cập nhanh đến giá trị tương ứng với khóa với độ phức tạp thời gian là O(1).

HashMap không chỉ được sử dụng thường xuyên trong phát triển hàng ngày mà còn là một trong những đối tượng quan trọng trong các cuộc phỏng vấn.

Dưới đây là một số thao tác cơ bản với HashMap:

1) Thêm phần tử:

Thêm một cặp khóa-giá trị vào HashMap bằng cách sử dụng phương thức put():

HashMap<String, Integer> map = new HashMap<>();
map.put("Tom", 20);
map.put("Jerry", 25);

2) Xóa phần tử:

Xóa một cặp khóa-giá trị từ HashMap bằng phương thức remove():

map.remove("Tom");

3) Sửa đổi phần tử:

Để sửa đổi giá trị của một khóa trong HashMap, bạn có thể sử dụng lại phương thức put(), vì mỗi khóa là duy nhất:

map.put("Tom", 30);

4) Tìm kiếm phần tử:

Để lấy giá trị từ HashMap, sử dụng phương thức get():

int age = map.get("Tom");

Trong các ứng dụng thực tế, HashMap thường được sử dụng để cache, chỉ mục và các tình huống tương tự. Ví dụ, bạn có thể sử dụng HashMap để lưu trữ thông tin người dùng với ID làm khóa và thông tin người dùng làm giá trị, hoặc lưu trữ chỉ mục tài liệu với từ khóa là từ khoá và danh sách ID tài liệu làm giá trị để tìm kiếm nhanh tài liệu.

Nguyên tắc triển khai của HashMap dựa trên bảng băm. Lớp dưới cùng của nó là một mảng. Mỗi vị trí của mảng có thể là một danh sách liên kết hoặc một cây đỏ đen hoặc có thể chỉ là một cặp khóa-giá trị (sẽ được thảo luận sau). Khi thêm cặp key-value, HashMap sẽ tính toán chỉ số mảng (chỉ mục) tương ứng với key dựa trên giá trị băm của key, sau đó chèn cặp key-value vào vị trí tương ứng.

Khi tra cứu một giá trị theo khóa, HashMap cũng sẽ tính chỉ số mảng dựa trên giá trị băm của khóa và tìm giá trị tương ứng.

01. Nguyên lý của phương thức hash

Sau khi hiểu đơn giản về HashMap, chúng ta sẽ bàn luận về câu hỏi đầu tiên: nguyên lý của phương thức hash, điều này sẽ giúp bạn hiểu rõ hơn về HashMap.

Hãy xem mã nguồn của phương thức hash trong HashMap của JDK 8:

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

Đoạn code này được sử dụng để làm gì?

Nó được sử dụng để xử lý giá trị hashCode của key, để đạt được giá trị băm cuối cùng.

Làm sao để hiểu câu này? Đừng vội vàng.

Hãy tạo một HashMap mới và thêm một phần tử bằng phương thức put.

HashMap<String, String> map = new HashMap<>();
map.put("chenmo", "沉默");

Hãy xem mã nguồn của phương thức put.

public V put(K key, V value) {
    return putVal(hash(key), key, value, false, true);
}

Bạn đã nhìn thấy sự xuất hiện của phương thức hash chưa?

Tác dụng của phương thức hash

Đầu tiên, nhớ rằng HashMap được triển khai bằng mảng và kích thước ban đầu của nó là 16 (chúng ta sẽ thảo luận về điều này sau).

HashMap khi thêm phần tử đầu tiên, cần xác định vị trí (index) trong mảng có kích thước là 16 dựa trên mã băm (hash code) của key. Như thế làm sao để xác định vị trí?

Để giúp bạn dễ hiểu hơn, mình đã vẽ một biểu đồ, có 16 ô vuông (bạn có thể hình dung chúng như các thùng), mỗi ô có một số thứ tự tương ứng với chỉ số (index) trong mảng có kích thước 16.

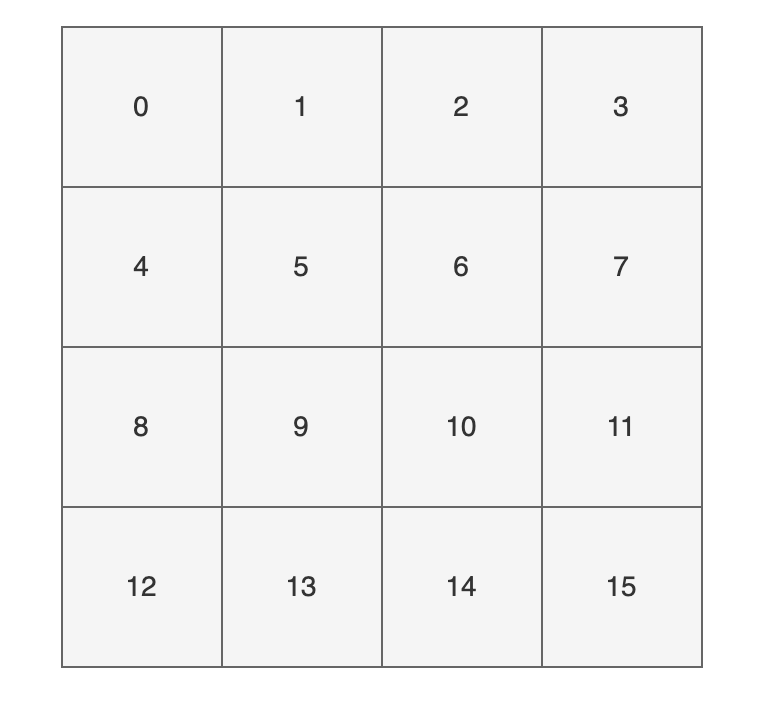
Bây giờ, chúng ta muốn đặt cặp key là "chenmo" và value là "沉默" vào 16 ô này. Làm sao để xác định vị trí (index)?

Tôi sẽ tiết lộ kết quả, vị trí tính toán của key "chenmo" là bao nhiêu?

Đáp án là 8, điều này có nghĩa là map.put("chenmo", "沉默") sẽ đặt cặp key là "chenmo" và value là "沉默" vào vị trí có index là 8 (cũng là thùng có index là 8).

Như vậy, bạn sẽ có một khái niệm rõ ràng hơn về cách HashMap lưu trữ các cặp key-value (phần tử). Phương thức hash có vai trò quan trọng trong việc tính toán vị trí của cặp key-value.

Quay lại phương thức hash:

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

Dưới đây là một số lời giải thích cho phương thức này:

Tham số key: Đó là key mà chúng ta muốn tính mã băm của nó.
key == null ? 0 : (h = key.hashCode()) ^ (h >>> 16): Đây là toán tử ba ngôi, nếu key là null thì mã băm sẽ là 0 (nghĩa là nó sẽ được đặt vào vị trí đầu tiên); nếu không, nó sẽ tính toán mã băm của key bằng cách gọi hashCode() và thực hiện phép XOR với mã băm dịch phải 16 bit.
Phép toán XOR (^): Đây là phép toán bitwise trong Java, nó so sánh từng bit của hai số, nếu bit là giống nhau thì kết quả là 0, nếu khác nhau thì là 1.
h >>> 16: Dịch phải mã băm 16 bit, tương đương với việc chia mã băm thành hai phần 16 bit.
Kết quả trả về là giá trị băm đã được tính toán.

Một dòng mã ngắn gọn này thể hiện sự thông minh của những nhà khoa học máy tính.

Lý thuyết cho thấy rằng, giá trị băm (hash code) là một số nguyên có dấu, trong khoảng từ -2147483648 đến 2147483648.

Tuy nhiên, một mảng có độ dài 40 tỷ ô nhớ không thể chứa được. Trước khi mở rộng, mảng ban đầu của HashMap có kích thước là 16, vì vậy giá trị băm này không thể được sử dụng trực tiếp, mà phải thực hiện phép AND với kích thước của mảng (như đã đề cập trước đó (n - 1) & hash), và sử dụng giá trị nhận được để truy cập chỉ số của mảng.

Phép chia lấy dư (Modulo) VS Phép chia lấy số dư (Remainder) VS Phép AND (Bitwise AND)

Ở đây tôi sẽ bổ sung một số kiến thức về phép chia lấy dư (Modulo)/lấy số dư (Remainder) và phép AND (AND operation).

Phép chia lấy dư (Modulo Operation) và phép chia lấy số dư (Remainder Operation), từ mặt nghiêm ngặt, là hai phương pháp tính toán khác nhau và cách thức triển khai của chúng trong máy tính cũng khác nhau.

Trong Java, thường sử dụng toán tử % để biểu diễn phép chia lấy số dư và sử dụng Math.floorMod() để biểu diễn phép chia lấy dư.

Khi cả hai toán hạng đều là số dương, kết quả của phép chia lấy dư và phép chia lấy số dư là giống nhau.
Chỉ khi có toán hạng âm, kết quả mới khác nhau.
Kết quả của phép chia lấy dư hướng về âm vô cùng; kết quả của phép chia lấy số dư hướng về 0. Đây là nguyên nhân cơ bản dẫn đến sự khác biệt giữa chúng khi xử lý các số âm.
Khi độ dài của mảng là 2 mũ n, hay là bội số của n, phép chia lấy dư/phép chia lấy số dư có thể được thay thế bằng phép AND (AND operation), hiệu quả hơn, bởi vì máy tính chỉ nhận dạng số nhị phân mà thôi.

Chúng ta sẽ xem xét một ví dụ cụ thể để hiểu hơn.

int a = -7;
int b = 3;

// Phép chia lấy số dư của a cho b
int remainder = a % b;
// Phép chia lấy dư của a cho b
int modulus = Math.floorMod(a, b);

System.out.println("Số: a = " + a + ", b = " + b);
System.out.println("Phép chia lấy số dư (%): " + remainder);
System.out.println("Phép chia lấy dư (Math.floorMod): " + modulus);

// Thay đổi dấu của a và b
a = 7;
b = -3;

remainder = a % b;
modulus = Math.floorMod(a, b);

System.out.println("\nSố: a = " + a + ", b = " + b);
System.out.println("Phép chia lấy số dư (%): " + remainder);
System.out.println("Phép chia lấy dư (Math.floorMod): " + modulus);

Kết quả đầu ra như sau:

Số: a = -7, b = 3
Phép chia lấy số dư (%): -1
Phép chia lấy dư (Math.floorMod): 2

Số: a = 7, b = -3
Phép chia lấy số dư (%): 1
Phép chia lấy dư (Math.floorMod): -2

Tại sao chúng ta lại có các kết quả như vậy?

Hãy xem xét trước hết về phép chia thông thường. Khi chúng ta chia một số cho một số khác, chúng ta sẽ có một phần dư và một phần dư.

Ví dụ, khi chia 7 cho 3, chúng ta có phần thương là 2 và phần dư là 1, bởi vì $(7 = 3 \times 2 + 1)$ .

Đề nghị đọc thêm: Java Modulo and Remainder

01. Phần dư:

Phần dư được định nghĩa dựa trên phép chia thông thường, vì vậy dấu của nó luôn giống với số bị chia. Phần thương hướng về 0.

Ví dụ, với -7 % 3, phần dư là -1. Điều này xảy ra vì -7 / 3 có thể có hai kết quả: một là phần thương -2 và phần dư -1; hai là phần thương -3 và phần dư 2. Vì phần dư hướng về 0, nên -2 gần với 0 hơn -3, do đó kết quả của phép chia lấy phần dư là -1.

02. Phép chia lấy dư:

Phép chia lấy dư cũng dựa trên phép chia, chỉ khác là dấu của nó luôn giống với số chia. Phần thương hướng về vô cùng âm.

Ví dụ, với Math.floorMod(-7, 3), kết quả là 2. Tương tự, -7 / 3 có thể có hai kết quả: một là phần thương -2 và phần dư -1; hai là phần thương -3 và phần dư 2. Vì phần thương hướng về vô cùng âm, nên -3 gần với vô cùng âm hơn -2, do đó kết quả của phép chia lấy phần dư là 2.

Cần lưu ý rằng, cho dù là phép chia lấy số dư hay phép chia lấy dư, số chia không thể là 0, vì cả hai đều dựa trên phép chia.

03. Phép AND:

Khi số bị chia và số chia đều là số dương, kết quả của phép chia lấy phần dư và phép chia lấy phần dư là giống nhau.

Ví dụ, phần dư của 7 chia cho 3 và phép chia lấy dư của 7 chia cho 3 đều là 1. Bởi vì cả hai đều dựa trên phép chia, phần thương của 7 chia cho 3 là 2 và phần dư là 1.

Do đó, chúng ta thường thấy rằng "phép chia lấy số dư" cũng có thể gọi là "phép chia lấy dư", điều này là không chính xác, dựa trên trường hợp số hạng bằng 0.

Đối với HashMap, nó cần sử dụng hash % table.length để xác định vị trí phần tử trong mảng, điều này giúp phân bố các phần tử một cách đồng đều trong mảng.

Ví dụ, nếu độ dài mảng là 3 và hash là 7, thì 7 % 3 cho kết quả là 1, nghĩa là phần tử có thể được đặt vào vị trí chỉ số là 1.

Khi hash là 8, 8 % 3 cho kết quả là 2, nghĩa là phần tử có thể được đặt vào vị trí chỉ số là 2.

Khi hash là 9, 9 % 3 cho kết quả là 0, nghĩa là phần tử có thể được đặt vào vị trí chỉ số là 0.

Điều này thật sự kỳ diệu, khi mảng có độ dài là 3, chúng ta có thể sử dụng hết 3 vị trí này.

Vậy tại sao HashMap khi tính chỉ số lại không sử dụng trực tiếp phép chia lấy số dư (hoặc phép chia lấy dư), mà lại sử dụng phép AND &?

Bởi vì khi độ dài của mảng là 2 mũ n (2^n), hash & (length - 1) = hash % length.

Ví dụ, 9 % 4 = 1, số nhị phân của 9 là 1001, 4 - 1 = 3, số nhị phân của 3 là 0011, 9 & 3 = 1001 & 0011 = 0001 = 1.

Tiếp tục với 10 % 4 = 2, số nhị phân của 10 là 1010, 4 - 1 = 3, số nhị phân của 3 là 0011, 10 & 3 = 1010 & 0011 = 0010 = 2.

Khi độ dài của mảng không phải là 2^n, kết quả của hash % length và hash & (length - 1) sẽ không giống nhau.

Ví dụ, 7 % 3 = 1, số nhị phân của 7 là 0111, 3 - 1 = 2, số nhị phân của 2 là 0010, 7 & 2 = 0111 & 0010 = 0010 = 2.

Vậy tại sao?

Đó là bởi vì từ góc nhìn của hệ thống nhị phân, phép chia $hash / length = hash / 2^n = hash >> n$ có thể thay thế bằng việc dịch phải n bit của hash, cho ta kết quả là phần nguyên của $hash / 2^n$ .

Phần dư, hay $hash \% 2^n$ , được xác định bởi các bit thấp nhất của biểu diễn nhị phân của hash. Điều này là do trong phép chia theo cơ số $2^n$ , chỉ có phần thấp hơn $2^n$ ảnh hưởng đến kết quả.

Ví dụ, với số 26 có biểu diễn nhị phân là 11010, để tính 26 % 8, trong đó 8 là $2^3$ , chúng ta chỉ quan tâm đến 3 bit thấp nhất của biểu diễn nhị phân của 26: 11010 có 3 bit thấp nhất là 010.

010 tương ứng với số 2 trong hệ thập phân, do đó kết quả của 26 % 8 là 2.

Khi thực hiện hash & (length - 1), chúng ta thực tế là giữ lại n bit thấp nhất của biểu diễn nhị phân của hash, và xóa bỏ các bit cao hơn.

Ví dụ, với hash = 14 và n = 3 (tức là độ dài mảng là $2^3$ , tức là 8):

  1110 (hash = 14)
& 0111 (length - 1 = 7)
  ----
  0110 (kết quả = 6)

Chỉ giữ lại 3 bit thấp nhất của 14, các bit cao hơn đã bị xóa bỏ.

Nhờ vào điều này, hai phép tính hash % length và hash & (length - 1) đã trở thành một hệ thống hoàn chỉnh. Trong máy tính, phép tính bitwise có tốc độ nhanh hơn rất nhiều so với phép chia lấy dư, vì máy tính hoạt động chủ yếu trên hệ thống nhị phân.

HashMap sử dụng phép chia lấy dư ở hai chỗ.

HashMap trong Java sử dụng phép tính (n - 1) & hash thay cho phép chia lấy dư % có hai trường hợp chính.

Khi thêm phần tử vào HashMap (qua phương thức putVal):

final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
    // Mảng
    HashMap.Node<K,V>[] tab;
    // Node
    HashMap.Node<K,V> p;

    // n là độ dài của mảng, i là chỉ số
    int n, i;
    // Nếu mảng rỗng
    if ((tab = table) == null || (n = tab.length) == 0)
        // Kích thước của mảng sau khi mở rộng lần đầu
        n = (tab = resize()).length;
    // Tính vị trí chèn nút, nếu vị trí đó trống, tạo một nút mới và chèn vào
    if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null);
}

Phép tính (n - 1) & hash được sử dụng để tính toán vị trí lưu trữ của phần tử dựa trên giá trị băm (hash) của khóa. Nó thay thế cho phép chia lấy dư %, sẽ được giải thích sau.

Khi truy xuất phần tử từ HashMap (qua phương thức getNode):

final Node<K,V> getNode(int hash, Object key) {
    // Lấy mảng và độ dài hiện tại, và nút đầu tiên của chuỗi nút (dựa trên chỉ số trực tiếp từ mảng)
    Node<K,V>[] tab;
    Node<K,V> first, e;
    int n;
    K k;
    if ((tab = table) != null && (n = tab.length) > 0 &&
            (first = tab[(n - 1) & hash]) != null) {
        // Nếu nút đầu tiên chính là nút cần tìm, trả về nút này
        if (first.hash == hash && ((k = first.key) == key || (key != null && key.equals(k))))
            return first;
        // Nếu nút đầu tiên không phải là nút cần tìm, duyệt qua chuỗi nút để tìm kiếm
        if ((e = first.next) != null) {
            do {
                if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k))))
                    return e;
            } while ((e = e.next) != null);
        }
    }
    // Nếu không tìm thấy nút tương ứng trong chuỗi nút, trả về null
    return null;
}

Lại xuất hiện phép tính (n - 1) & hash, thực hiện để xác định vị trí của phần tử cần truy xuất dựa trên giá trị băm (hash).

Phép tính này (n - 1) & hash thay thế cho phép chia lấy dư %, được áp dụng vì:

Nó nhanh hơn phép chia lấy dư % trong các máy tính hiện đại, đặc biệt là khi n là một số lũy thừa của 2 (như 16, 32, 64,...).
Phép & chỉ yêu cầu các phép toán bitwise, nó cực kỳ nhanh chóng so với phép chia lấy dư %.
Điều này cải thiện hiệu suất của HashMap khi thực hiện các thao tác thêm, truy xuất và xóa phần tử.

Do đó, trong HashMap của Java, sử dụng phép & là một chiến lược tối ưu để tính toán vị trí lưu trữ của các phần tử dựa trên giá trị băm.

Phép chia lấy số dư % và phép AND &

Có lẽ mọi người sẽ tự hỏi: Tại sao không sử dụng phép chia lấy dư % mà lại chọn phép AND & ở đây nhỉ?

Điều này là vì phép AND & nhanh hơn so với phép % và khi b là một lũy thừa của 2, có một mối quan hệ toán học như sau.

$a \% b = a \& (b-1)$

Nếu thay bằng $2^n$ , thì công thức trở thành:

$a \% ( 2^n ) = a \& (2^n - 1)$

Hãy xem xét một ví dụ, giả sử $a = 14$ , $b = 8$ , tức là $2^3$ , $n = 3$ .

14 % 8 (dư là 6).

14 ở hệ nhị phân là 1110, 8 ở hệ nhị phân là 1000, 8-1 = 7, 7 ở hệ nhị phân là 0111, 1110 & 0111 = 0110, tức là $0\times 2^0 + 1 \times 2^1 + 1 \times 2^2 + 0 \times 2^3= 0 + 2 + 4 + 0 = 6$ , nên 14%8 cũng bằng 6.

Như vậy, máy tính làm việc như vậy, không thể thay đổi được, 😝

Điều này cũng giải thích tại sao độ dài của mảng trong HashMap nên là lũy thừa của 2.

Vì sao lại như thế?

Bởi vì (độ dài của mảng - 1) chính là một "mặt nạ" low bits - các bit cuối cùng của nó thường là 1, giúp cho phép & có ý nghĩa, còn kết quả là 0.

Kết quả của phép toán a&b là: nếu các bit tương ứng trong a và b đồng thời là 1 thì bit kết quả tương ứng là 1, ngược lại là 0. Ví dụ: 5&3=1, số nhị phân của 5 là 0101, số nhị phân của 3 là 0011, 5&3=0001=1.

luỹ thừa của 2 là số chẵn, số chẵn trừ đi 1 là số lẻ, và bit cuối cùng của số lẻ là 1, đảm bảo rằng hash &(length-1) có thể kết thúc bằng 0 hoặc 1 (phụ thuộc vào giá trị của hash), nghĩa là kết quả của phép & có thể là số chẵn hoặc số lẻ, điều này giúp phân phối đều các giá trị hash.

Nói một cách khác, phép & làm cho các bit cao của giá trị hash trở thành 0, chỉ giữ lại các giá trị bit thấp.

Giả sử giá trị hash nhị phân là 10100101 11000100 00100101, chúng ta thử áp dụng phép & với nó. Độ dài ban đầu của HashMap là 16, 16-1=15, biểu diễn nhị phân là 00000000 00000000 00001111 (các bit cao được điền vào bằng 0):

	 10100101 11000100 00100101
&	 00000000 00000000 00001111
----------------------------------
	 00000000 00000000 00000101

Do 15 có các bit cao là 0, kết quả của phép & cũng chắc chắn là 0 ở bit cao, chỉ còn lại 4 bit thấp 0101, tương đương với số thập phân 5.

Vì vậy, giá trị hash 10100101 11000100 00100101 sẽ được đặt vào vị trí thứ 5 trong mảng.

Dù bạn có là người mới, bạn vẫn có thể hiểu rằng phép & được sử dụng để tính chỉ số của mảng.

Khi thực hiện put, tính chỉ số, đặt cặp khóa giá trị vào thùng tương ứng.
Khi thực hiện get, thông qua chỉ số, lấy cặp khóa giá trị từ thùng tương ứng.

Tại sao lại gọi phương thức hash trước khi thực hiện phép chia lấy dư?

Hãy xem hình dưới đây.

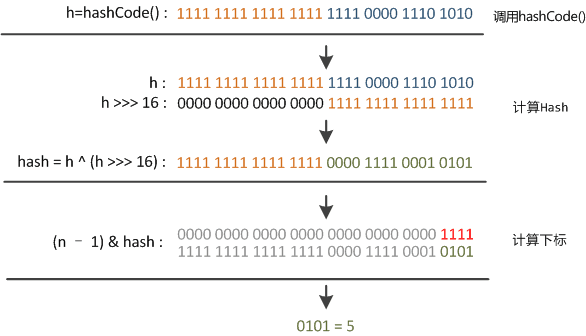
Giả sử giá trị hash của một khóa là 11111111 11111111 11110000 1110 1010, sau khi dịch phải 16 bit (h >>> 16), chính là 00000000 00000000 11111111 11111111, sau khi thực hiện phép XOR (h ^ (h >>> 16)), kết quả là 11111111 11111111 00001111 00010101.

Phép XOR (^) là phép toán dựa trên các bit nhị phân, có ký hiệu là XOR hoặc ^, với quy tắc phép toán như sau: Nếu hai bit cùng một giá trị, kết quả là 0, nếu khác nhau, kết quả là 1.

Bằng cách kết hợp bit cao và bit thấp của giá trị hash ban đầu, sự ngẫu nhiên của bit thấp được tăng cường (bằng cách thêm vào một phần đặc trưng của bit cao). Kết quả sau đó được thực hiện phép & với (độ dài mảng - 1) (00000000 00000000 00001111), cho ta chỉ số là 00000000 00000000 00000101, tức là 5.

Hãy nhớ lại ví dụ trước đó của chúng ta với giá trị hash 10100101 11000100 00100101. Trước khi gọi phương thức hash, kết quả phép chia lấy dư với 15 cũng là 5. Bây giờ hãy xem kết quả phép chia lấy dư sau khi gọi phương thức hash.

Giá trị hash 00000000 10100101 11000100 00100101 (bổ sung 32 bit), sau khi dịch phải 16 bit (h >>> 16) là 00000000 00000000 00000000 10100101, sau phép XOR (h ^ (h >>> 16)) là 00000000 10100101 00111011 10000000.

Kết quả sau đó được thực hiện phép & với (độ dài mảng - 1) (00000000 00000000 00001111), cho ta chỉ số là 00000000 00000000 00000000, tức là 0.

Tóm lại, phương thức hash được sử dụng để tối ưu hóa giá trị hash, dịch phải giá trị hash 16 bit, tức là chính nó độ dài của một nửa, sau đó thực hiện phép XOR với giá trị hash ban đầu để hỗn hợp giá trị cao và thấp của hash, tăng tính ngẫu nhiên.

Nói một cách đơn giản, phương thức hash giúp tăng tính ngẫu nhiên, giúp phân bố các phần tử dữ liệu một cách đồng đều hơn, giảm thiểu các va chạm.

Dưới đây là đoạn mã kiểm tra mà tôi viết, giả sử độ dài ban đầu của HashMap là 16 sau khi mở rộng lần đầu tiên, tôi đã đặt năm cặp khóa-giá trị vào đó để xem giá trị hash của khóa (sau khi tính toán bằng phương thức hash()) và chỉ số (sau khi thực hiện phép chia lấy dư).

HashMap<String, String> map = new HashMap<>();
map.put("chenmo", "沉默");
map.put("wanger", "王二");
map.put("chenqingyang", "陈清扬");
map.put("xiaozhuanling", "小转铃");
map.put("fangxiaowan", "方小婉");

// Duyệt qua HashMap
for (String key : map.keySet()) {
    int h, n = 16;
    int hash = (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
    int i = (n - 1) & hash;
    // In ra giá trị hash và chỉ số i của khóa
    System.out.println("Giá trị hash của " + key + " là: " + hash + " và chỉ số i là: " + i);
}

Kết quả xuất ra như sau:

Giá trị hash của xiaozhuanling là: 14597045 và chỉ số i là: 5
Giá trị hash của fangxiaowan là: -392727066 và chỉ số i là: 6
Giá trị hash của chenmo là: -1361556696 và chỉ số i là: 8
Giá trị hash của chenqingyang là: -613818743 và chỉ số i là: 9
Giá trị hash của wanger là: -795084437 và chỉ số i là: 11

Nói cách khác, trong trường hợp này, không có xung đột hash xảy ra, các chỉ số là khá phân bố đều, là 5, 6, 8, 9 và 11. Điều này chủ yếu nhờ vào phương thức hash.

Tóm tắt

Phương thức hash có vai trò chính là xử lý giá trị hashCode của key, từ đó thu được giá trị băm cuối cùng. Bởi vì giá trị hashCode của key là không xác định, có thể xảy ra va chạm băm, do đó cần phải ánh xạ giá trị băm này vào vị trí lưu trữ thực tế của HashMap thông qua một thuật toán nhất định.

Nguyên lý của phương thức hash là đầu tiên lấy giá trị hashCode của đối tượng key, sau đó thực hiện phép XOR giữa các bit cao và thấp của nó để thu được một giá trị băm mới. Tại sao lại sử dụng phép XOR? Bởi vì phân bố của các bit cao và thấp trong giá trị hashCode là khá đồng đều. Nếu chỉ đơn giản cộng chúng hoặc thực hiện phép toán bit, có thể dễ dàng xảy ra va chạm băm, trong khi phép XOR có thể tránh được vấn đề này.

Tiếp theo, giá trị băm mới này được thực hiện phép lấy dư (mod), từ đó thu được vị trí lưu trữ thực tế. Mục đích của phép lấy dư này là ánh xạ giá trị băm vào chỉ số của thùng (bucket) trong HashMap. Mỗi thùng trong mảng của HashMap sẽ lưu trữ một danh sách liên kết (hoặc cây đỏ đen), chứa các cặp key-value có cùng giá trị băm (nếu không có giá trị băm giống nhau thì chỉ lưu trữ một cặp key-value).

Tổng kết lại, phương thức hash của HashMap có nhiệm vụ là xử lý giá trị hashCode của đối tượng key, từ đó thu được giá trị băm cuối cùng và ánh xạ nó vào vị trí lưu trữ thực tế trong HashMap. Quá trình này quyết định hiệu suất tìm kiếm các cặp key-value trong HashMap.

02. Cơ chế mở rộng của HashMap

Sau khi hiểu được phương thức hash, chúng ta sẽ tiếp tục đi sâu vào vấn đề thứ hai, đó là cơ chế mở rộng của HashMap.

Chúng ta đều biết rằng mảng khi đã khởi tạo kích thước thì không thể thay đổi được, do đó đã có các cấu trúc dữ liệu như ArrayList là "mảng động", có thể tự động mở rộng.

HashMap dùng mảng làm nền tảng. Khi thêm các phần tử vào HashMap mà mảng không còn đủ chỗ để chứa thêm nữa, ta cần phải mở rộng mảng để có thể chứa thêm các phần tử mới; ngoài ra, việc tăng dung lượng cũng sẽ tăng hiệu suất truy vấn tương ứng, vì có nhiều "thùng" hơn, những phần tử trước đây cần lưu trong danh sách liên kết (hoặc cây đỏ đen khi cần thiết để tối ưu) có thể có "thùng" riêng biệt (có thể truy cập trực tiếp).

Xem xét ví dụ sau, ta đặt dung lượng ban đầu là 16:

HashMap<String, String> map = new HashMap<>();
map.put("chenmo", "沉默");
map.put("wanger", "王二");
map.put("chenqingyang", "陈清扬");
map.put("xiaozhuanling", "小转铃");
map.put("fangxiaowan", "方小婉");
map.put("yexin", "叶辛");
map.put("liuting","刘婷");
map.put("yaoxiaojuan","姚小娟");

// Duyệt qua HashMap
for (String key : map.keySet()) {
    int h, n = 16;
    int hash = (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
    int i = (n - 1) & hash;
    // In ra giá trị hashCode của key và chỉ số i
    System.out.println(key + " có hashCode : " + hash +" và chỉ số : " + i);
}

Kết quả in ra như sau:

liuting có hashCode : 183821170 và chỉ số : 2
xiaozhuanling có hashCode : 14597045 và chỉ số : 5
fangxiaowan có hashCode : -392727066 và chỉ số : 6
yaoxiaojuan có hashCode : 1231568918 và chỉ số : 6
chenmo có hashCode : -1361556696 và chỉ số : 8
chenqingyang có hashCode : -613818743 và chỉ số : 9
yexin có hashCode : 114873289 và chỉ số : 9
wanger có hashCode : -795084437 và chỉ số : 11

Nhìn vào đấy:

fangxiaowan và yaoxiaojuan có chỉ số là 6;
chenqingyang và yexin có chỉ số là 9.

Điều này có nghĩa là, ta sẽ dùng phương pháp đan xen (sẽ giải thích sau) để cho chúng vào cùng một chỉ số. Khi tra cứu, không thể truy cập trực tiếp bằng cách chỉ định chỉ số (O(1) thời gian phức tạp), mà phải duyệt qua (O(n) thời gian phức tạp).

Nếu tăng kích thước mảng từ 16 lên 32 thì sao?

Đơn giản là thay đổi n từ 16 thành 32 trong ví dụ trước sẽ cho kết quả sau:

liuting có hashCode : 183821170 và chỉ số : 18
xiaozhuanling có hashCode : 14597045 và chỉ số : 21
fangxiaowan có hashCode : -392727066 và chỉ số : 6
yaoxiaojuan có hashCode : 1231568918 và chỉ số : 22
chenmo có hashCode : -1361556696 và chỉ số : 8
chenqingyang có hashCode : -613818743 và chỉ số : 9
yexin có hashCode : 114873289 và chỉ số : 9
wanger có hashCode : -795084437 và chỉ số : 11

Có thể thấy:

Mặc dù chenqingyang và yexin vẫn có chỉ số là 9.
Nhưng fangxiaowan có chỉ số là 6, yaoxiaojuan có chỉ số từ 6 tăng lên 22, mỗi người đều có chỗ trống.

Tuy nhiên, mảng không tự mở rộng, vì vậy nếu bạn muốn mở rộng, bạn cần tạo một mảng lớn hơn, sau đó sao chép các thành phần từ mảng nhỏ hơn và bạn cần phải tính lại giá trị băm và phân phối lại các thùng (tính lại phân bố) thời gian này cũng hao phí.

Phương thức resize

Quá trình mở rộng của HashMap được thực hiện thông qua phương thức resize. Trên JDK 8, nó đã tích hợp cây đỏ đen (khi độ dài của danh sách vượt quá 8, danh sách sẽ được chuyển thành cây đỏ đen để tăng hiệu suất truy vấn), điều này có thể khó hiểu đối với người mới.

Để giảm áp lực học tập, chúng ta có thể sử dụng mã nguồn của JDK 7 để hiểu rõ hơn. Sau đó, khi nhìn vào JDK 8, mọi thứ sẽ trở nên dễ dàng hơn nhiều.

Hãy xem mã nguồn phương thức resize trong Java 7, tôi đã thêm chú thích:

// newCapacity là dung lượng mới
void resize(int newCapacity) {
    // oldTable là mảng nhỏ, là bộ nhớ tạm thời
    Entry[] oldTable = table;
    // oldCapacity là dung lượng cũ
    int oldCapacity = oldTable.length;
    // MAXIMUM_CAPACITY là dung lượng tối đa, 2 mũ 30 = 1<<30
    if (oldCapacity == MAXIMUM_CAPACITY) {
        // Dung lượng được điều chỉnh thành giá trị lớn nhất của Integer, 0x7fffffff (hệ số hexa) = 2 mũ 31 - 1
        threshold = Integer.MAX_VALUE;
        return;
    }

    // Khởi tạo một mảng mới (dung lượng lớn)
    Entry[] newTable = new Entry[newCapacity];
    // Chuyển các phần tử từ mảng nhỏ sang mảng lớn
    transfer(newTable, initHashSeedAsNeeded(newCapacity));
    // Tham chiếu đến mảng lớn mới
    table = newTable;
    // Tính toán lại ngưỡng
    threshold = (int)Math.min(newCapacity * loadFactor, MAXIMUM_CAPACITY + 1);
}

Phương thức này nhận đầu vào là dung lượng mới newCapacity và mở rộng dung lượng của HashMap lên newCapacity.

Đầu tiên, phương thức lấy mảng cũ oldTable và dung lượng cũ oldCapacity của HashMap hiện tại. Nếu dung lượng cũ đã đạt đến dung lượng tối đa mà HashMap hỗ trợ MAXIMUM_CAPACITY (2^30), ngưỡng mới threshold sẽ được đặt là Integer.MAX_VALUE (2 mũ 31 - 1), bởi vì dung lượng của HashMap không thể vượt quá MAXIMUM_CAPACITY.

Sau đó, phương thức tạo ra một mảng mới newTable và chuyển các phần tử từ mảng cũ oldTable sang mảng mới newTable. Quá trình chuyển đổi được thực hiện bằng cách gọi phương thức transfer. Phương thức này duyệt qua từng bucket trong mảng cũ và sau khi tính lại giá trị băm của mỗi cặp khóa-giá trị, chèn chúng vào bucket tương ứng trong mảng mới.

Khi quá trình chuyển đổi hoàn tất, phương thức thay đổi tham chiếu mảng trong HashMap từ mảng cũ table sang mảng mới newTable, và tính toán lại ngưỡng threshold. Ngưỡng mới được tính là giá trị nhỏ hơn giữa newCapacity * loadFactor và MAXIMUM_CAPACITY + 1, nhưng nếu kết quả tính toán vượt quá dung lượng tối đa MAXIMUM_CAPACITY mà HashMap hỗ trợ, thì ngưỡng sẽ được đặt là MAXIMUM_CAPACITY + 1, bởi vì số lượng phần tử trong HashMap không thể vượt quá MAXIMUM_CAPACITY.

Dung lượng mới newCapacity

Vậy newCapacity được tính toán như thế nào?

Trong JDK 7, newCapacity được khởi tạo bằng hai lần dung lượng cũ oldCapacity. Sau đó, nó sẽ được điều chỉnh dựa trên các điều kiện sau:

int newCapacity = oldCapacity * 2;
if (newCapacity < 0 || newCapacity >= MAXIMUM_CAPACITY) {
    newCapacity = MAXIMUM_CAPACITY;
} else if (newCapacity < DEFAULT_INITIAL_CAPACITY) {
    newCapacity = DEFAULT_INITIAL_CAPACITY;
}

Nếu newCapacity tính toán vượt quá giới hạn dung lượng tối đa của HashMap MAXIMUM_CAPACITY (tức là 2^30), thì newCapacity sẽ được đặt lại bằng MAXIMUM_CAPACITY. Ngoài ra, nếu newCapacity nhỏ hơn dung lượng khởi tạo mặc định DEFAULT_INITIAL_CAPACITY (tức là 16), thì newCapacity sẽ được đặt lại bằng DEFAULT_INITIAL_CAPACITY. Điều này giúp tránh tình trạng newCapacity quá nhỏ hoặc quá lớn dẫn đến nhiều xung đột băm hoặc lãng phí không gian.

Trong JDK 8, cách tính toán newCapacity đã có một số thay đổi nhỏ:

int newCapacity = oldCapacity << 1;
if (newCapacity >= DEFAULT_INITIAL_CAPACITY && oldCapacity >= DEFAULT_INITIAL_CAPACITY) {
    if (newCapacity > MAXIMUM_CAPACITY)
        newCapacity = MAXIMUM_CAPACITY;
} else {
    if (newCapacity < DEFAULT_INITIAL_CAPACITY)
        newCapacity = DEFAULT_INITIAL_CAPACITY;
}

Ở đây, oldCapacity << 1 thay thế cho oldCapacity * 2, điều này sử dụng toán tử dịch trái (<<).

Đây là phần giới thiệu ngắn gọn:

a=39
b = a << 2

Số thập phân 39 được biểu thị dưới dạng nhị phân 8 chữ số, là 00100111. Sau khi dịch hai vị trí sang trái, nó là 10011100 (các bit thấp được điền bằng 0), sau đó được chuyển đổi thành số thập phân, là 156.

Các phép tính dịch chuyển thường có thể được sử dụng để thay thế các phép tính nhân và chia. Ví dụ: dịch chuyển 0010011 (39) sang trái hai vị trí sẽ trở thành 10011100 (156), chính xác gấp 4 lần giá trị ban đầu.

Trên thực tế, sau khi dịch số nhị phân sang trái, nó sẽ gấp 2, 4 hoặc 8 lần giá trị ban đầu. Và ngược lại dịch sang phải sẽ là chia 2, 4, 8, ... Chỉ cần nhớ điều này.

Phương thức transfer

Tiếp theo, hãy nói về phương thức transfer, phương thức này được sử dụng để chuyển đổi các phần tử từ mảng nhỏ cũ sang mảng lớn mới.

void transfer(Entry[] newTable, boolean rehash) {
    // Dung lượng mới của mảng
    int newCapacity = newTable.length;
    // Duyệt qua mảng nhỏ cũ
    for (Entry<K,V> e : table) {
        while(null != e) {
            // Lấy phần tử tiếp theo trong chuỗi (chain)
            Entry<K,V> next = e.next;
            // Nếu cần tính lại hash
            if (rehash) {
                e.hash = null == e.key ? 0 : hash(e.key);
            }
            // Tính chỉ số i trong mảng mới dựa trên hash của key và dung lượng mới
            int i = indexFor(e.hash, newCapacity);

            // Đưa phần tử mới vào đầu danh sách tại vị trí i trong mảng mới
            e.next = newTable[i];
            newTable[i] = e;

            // Tiếp tục với phần tử tiếp theo trong chuỗi
            e = next;
        }
    }
}

Phương thức này nhận vào một mảng mới newTable và một giá trị boolean rehash, trong đó newTable đại diện cho bảng băm mới và rehash xác định xem có cần tính lại giá trị băm cho các khóa không.

Trong phương thức, đầu tiên lấy ra dung lượng mới newCapacity của mảng newTable. Tiếp theo, phương thức duyệt qua từng phần tử e trong mảng table (mảng cũ). Đối với mỗi phần tử e, nó sử dụng phương pháp chuỗi (chain) để lưu trữ các giá trị khác nhau của cùng một khóa. Nếu rehash là true, phương thức tính lại giá trị băm của khóa và lưu giữ trong thuộc tính hash của e.

Tiếp theo, phương thức tính chỉ số i trong mảng mới dựa trên giá trị băm e.hash và newCapacity.

Sau đó, phương thức thêm phần tử e vào đầu danh sách tại vị trí i trong mảng mới newTable. Cụ thể là đặt e.next thành phần tử đầu tiên của danh sách hiện tại tại vị trí i, và sau đó gán e là phần tử đầu tiên của danh sách tại vị trí i trong newTable.

Cuối cùng, phương thức tiếp tục với phần tử tiếp theo trong chuỗi (nếu có) bằng cách gán e bằng next, và lặp lại quá trình cho đến khi hết chuỗi của phần tử hiện tại.

Khi phương thức kết thúc, tất cả các phần tử từ mảng cũ table đã được chuyển sang mảng mới newTable, hoàn tất quá trình chuyển đổi.

Phương pháp Chaining

Xin lưu ý rằng e.next = newTable[i] sử dụng phương thức chèn vào đầu của danh sách liên kết đơn. Điều này có nghĩa là mỗi khi có phần tử mới tại cùng một vị trí, phần tử mới này sẽ luôn được đặt ở đầu danh sách. Điều này dẫn đến việc các phần tử được thêm vào đầu của danh sách sẽ cuối cùng được đưa lên cuối danh sách.

Tuy nhiên, điều này có thể gây ra một vấn đề: các phần tử trên cùng một chuỗi trong mảng cũ, sau khi tính lại vị trí chỉ mục, có thể được đặt vào các vị trí khác nhau trong mảng mới.

Để giải quyết vấn đề này, Java 8 đã có những cải tiến đáng kể (sẽ được thảo luận khi nói đến quá trình mở rộng).

Mở rộng trong Java 8

Mã nguồn mở rộng của JDK 8:

final Node<K,V>[] resize() {
    Node<K,V>[] oldTab = table; // Lấy mảng cũ table
    int oldCap = (oldTab == null) ? 0 : oldTab.length; // Lấy độ dài của mảng cũ oldCap
    int oldThr = threshold; // Lấy ngưỡng threshold
    int newCap, newThr = 0;
    if (oldCap > 0) { // Nếu mảng cũ table không rỗng
        if (oldCap >= MAXIMUM_CAPACITY) { // Nếu độ dài mảng cũ vượt quá MAXIMUM_CAPACITY, chỉ định ngưỡng là Integer.MAX_VALUE và trả về mảng cũ
            threshold = Integer.MAX_VALUE;
            return oldTab;
        }
        else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY && // Nếu độ dài mảng mới không vượt quá MAXIMUM_CAPACITY và oldCap lớn hơn hoặc bằng DEFAULT_INITIAL_CAPACITY
                 oldCap >= DEFAULT_INITIAL_CAPACITY)
            newThr = oldThr << 1; // double threshold
    }
    else if (oldThr > 0) // initial capacity was placed in threshold
        newCap = oldThr;
    else { // zero initial threshold signifies using defaults
        newCap = DEFAULT_INITIAL_CAPACITY;
        newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
    }
    // Tính toán giới hạn mở rộng mới
    if (newThr == 0) {
        float ft = (float)newCap * loadFactor;
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                  (int)ft : Integer.MAX_VALUE);
    }
    threshold = newThr; // Gán ngưỡng mở rộng mới cho thành viên threshold
    @SuppressWarnings({"rawtypes","unchecked"})
        Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap]; // Tạo mảng mới newTab
    table = newTab; // Gán mảng mới newTab cho thành viên table
    if (oldTab != null) { // Nếu mảng cũ oldTab không rỗng
        for (int j = 0; j < oldCap; ++j) { // Duyệt qua từng phần tử của mảng cũ
            Node<K,V> e;
            if ((e = oldTab[j]) != null) { // Nếu phần tử này không rỗng
                oldTab[j] = null; // Gán phần tử tại vị trí j của mảng cũ thành null để thu gom rác
                if (e.next == null) // Nếu phần tử này không có va chạm
                    newTab[e.hash & (newCap - 1)] = e; // Đưa phần tử này vào mảng mới
                else if (e instanceof TreeNode) // Nếu phần tử này là TreeNode
                    ((TreeNode<K,V>)e).split(this, newTab, j, oldCap); // Chia phần tử TreeNode này thành hai danh sách liên kết
                else { // Nếu phần tử này là danh sách liên kết
                    Node<K,V> loHead = null, loTail = null; // Đầu và đuôi của danh sách liên kết thấp
                    Node<K,V> hiHead = null, hiTail = null; // Đầu và đuôi của danh sách liên kết cao
                    Node<K,V> next;
                    do { // Duyệt qua danh sách liên kết này
                        next = e.next;
                        if ((e.hash & oldCap) == 0) { // Nếu phần tử này thuộc danh sách liên kết thấp
                            if (loTail == null) // Nếu danh sách liên kết thấp chưa có phần tử
                                loHead = e; // Đặt phần tử này làm đầu danh sách liên kết thấp
                            else
                                loTail.next = e; // Nếu danh sách liên kết thấp đã có phần tử, thêm phần tử này vào cuối danh sách liên kết thấp
                            loTail = e; // Cập nhật đuôi của danh sách liên kết thấp
                        }
                        else { // Nếu phần tử này thuộc danh sách liên kết cao
                            if (hiTail == null) // Nếu danh sách liên kết cao chưa có phần tử
                                hiHead = e; // Đặt phần tử này làm đầu danh sách liên kết cao
                            else
                                hiTail.next = e; // Nếu danh sách liên kết cao đã có phần tử, thêm phần tử này vào cuối danh sách liên kết cao
                            hiTail = e; // Cập nhật đuôi của danh sách liên kết cao
                        }
                    } while ((e = next) != null); //
                    if (loTail != null) { // Nếu danh sách liên kết thấp không rỗng
                        loTail.next = null; // Gán đuôi của danh sách liên kết thấp thành null để thu gom rác
                        newTab[j] = loHead; // Đưa danh sách liên kết thấp vào vị trí tương ứng của mảng mới
                    }
                    if (hiTail != null) { // Nếu danh sách liên kết cao không rỗng
                        hiTail.next = null; // Gán đuôi của danh sách liên kết cao thành null để thu gom rác
                        newTab[j + oldCap] = hiHead; // Đưa danh sách liên kết cao vào vị trí tương ứng của mảng mới
                    }
                }
            }
        }
    }
    return newTab; // Trả về mảng mới
}

Lấy mảng cũ table, độ dài của mảng oldCap, và ngưỡng oldThr.
Nếu mảng cũ table không rỗng, tính toán độ dài mảng mới newCap và ngưỡng mới newThr dựa trên quy tắc mở rộng và sao chép các phần tử từ mảng cũ sang mảng mới.
Nếu mảng cũ table rỗng nhưng ngưỡng oldThr lớn hơn 0, độ dài mảng mới newCap sẽ là ngưỡng cũ oldThr.
Nếu cả mảng cũ table và ngưỡng oldThr đều bằng 0, điều này cho thấy HashMap được tạo bằng constructor không tham số, vì vậy tính toán mặc định cho độ dài mảng DEFAULT_INITIAL_CAPACITY (16) và ngưỡng mở rộng DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY.
Tính toán ngưỡng mở rộng threshold mới và gán cho biến thành viên threshold.
Tạo mảng mới newTab và gán cho biến thành viên table.
Nếu mảng cũ oldTab không rỗng, sao chép các phần tử từ mảng cũ sang mảng mới và xử lý va chạm bằng cách chia phần tử TreeNode hoặc danh sách liên kết.
Trả về mảng mới newTab.

Trong JDK 7, phương thức để xác định vị trí của phần tử trong HashMap được thực hiện như sau:

static int indexFor(int h, int length) {
    // assert Integer.bitCount(length) == 1 : "length must be a non-zero power of 2";
    return h & (length-1);
}

Phương thức này thực chất là thực hiện phép AND bit giữa giá trị hash của key h và độ dài của mảng length, tương đương với phép h % length (chia lấy dư). Phương thức này được sử dụng để tính toán vị trí của phần tử trong mảng dựa trên giá trị hash của key.

Giờ chúng ta đi phân tích trường hợp trước và sau khi mở rộng mảng, giả sử độ dài mảng table ban đầu là 2 và hệ số tải loadFactor là 1, tức là khi số lượng phần tử vượt quá độ dài của mảng thì thực hiện mở rộng.

Tình huống ban đầu:

Độ dài mảng table.length = 2, và các key có giá trị hash lần lượt là 3, 7, 5.

Sau thao tác modulo, một xung đột băm đã xảy ra trên các key và tất cả chúng đều vào table[1]. Vì vậy, đây là những gì nó trông giống như trước khi mở rộng.

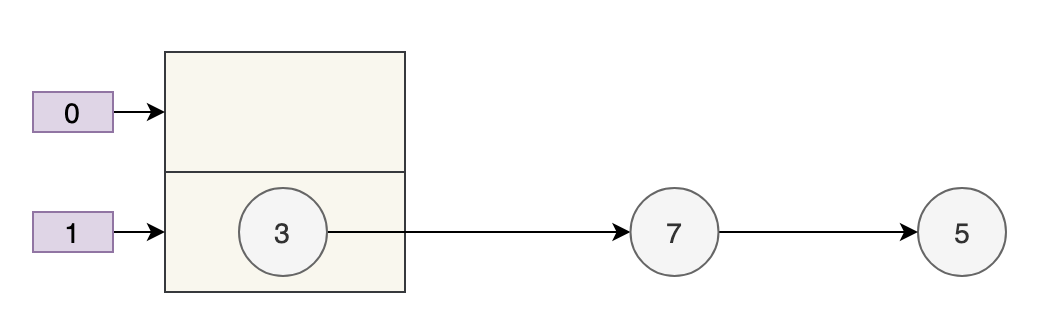
Dung lượng của mảng là 2 và các phần tử có khóa 3, 7 và 5 đều vào table[1] và xung đột băm cần được giải quyết thông qua phương pháp chaining.

Hệ số tải LoadFactor là 1, nghĩa là việc mở rộng được thực hiện khi số phần tử lớn hơn độ dài của bảng.

Sau khi mở rộng, độ dài mảng table tăng lên 4.

Key 3 sau khi tính toán 3 % 4 là 3, được đặt vào table[3].
Key 7 sau khi tính toán 7 % 4 là 3, được đặt vào đầu danh sách liên kết của table[3].
Key 5 sau khi tính toán 5 % 4 là 1, được đặt vào table[1].

Key 7 di chuyển trước 3 vì JDK 7 sử dụng phương pháp chèn đầu.

e.next = newTable[i];

Đồng thời, key 5 mở rộng di chuyển đến vị trí có chỉ số 1.

Trong tình huống tốt nhất, sau khi mở rộng, key 7 sẽ được đặt sau key 3, và key 5 sẽ được đặt sau key 7, giữ nguyên thứ tự ban đầu.

JDK 8 hoàn toàn đảo ngược tình trạng này, vì thuật toán băm của JDK 8 đã được tối ưu hóa và khi độ dài mảng là lũy thừa của 2, nó có thể giải quyết một cách khéo léo các vấn đề gặp phải trong JDK 7.

Mã mở rộng cho JDK 8 như sau:

Node<K,V>[] newTab = new Node[newCapacity];
for (int j = 0; j < oldTab.length; j++) {
    Node<K,V> e = oldTab[j];
    if (e != null) {
        int hash = e.hash;
        int newIndex = hash & (newCapacity - 1); // Tính vị trí mới trong mảng mới
        // Di chuyển nút vào vị trí tương ứng trong mảng mới
        newTab[newIndex] = e;
    }
}

Ở đây, cách tính vị trí mới là hash & (newCapacity - 1), tương tự như JDK 7 h & (length-1). Phần khác biệt chủ yếu nằm ở hàm băm trong JDK 8:

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

Đoạn mã này thực hiện việc lấy giá trị hash 32 bit của key key.hashCode() và thực hiện phép XOR với kết quả của phép dịch phải không dấu 16 bit của h. Điều này giúp phân tán các giá trị hash của các key khác nhau một cách hiệu quả hơn, giảm thiểu xung đột và cải thiện hiệu suất của HashMap.

JDK 7 giống thế này:

final int hash(Object k) {
    int h = hashSeed;
    if (0 != h && k instanceof String) {
        return sun.misc.Hashing.stringHash32((String) k);
    }

    h ^= k.hashCode();

    // This function ensures that hashCodes that differ only by
    // constant multiples at each bit position have a bounded
    // number of collisions (approximately 8 at default load factor).
    h ^= (h >>> 20) ^ (h >>> 12);
    return h ^ (h >>> 7) ^ (h >>> 4);
}

Nếu sử dụng thuật toán băm của JDK 8 để tính giá trị băm, chúng ta sẽ tìm thấy điều gì đó đặc biệt.

Giả sử trước khi mở rộng, độ dài mảng là 16 (n-1 là 0000 1111), và các key có hash như sau: key1 là 5 (0000 0101), key2 là 21 (0001 0101).

key1 & (n-1) cho kết quả là 0000 0101, tức là 5.
key2 & (n-1) cho kết quả là 0000 0101, tức là 5.
Tại thời điểm này, có xung đột băm và phương pháp chaining được sử dụng để giải quyết xung đột băm.

Khi mảng được mở rộng lên gấp đôi, tức là 32 (n-1 là 0001 1111):

key1 & (n-1) cho kết quả là 0000 0101, tức là 5.
key2 & (n-1) cho kết quả là 0001 0101, tức là 21 (5 + 16), tại vị trí gấp đôi của vị trí trong mảng cũ.

Thật tuyệt vời phải không?

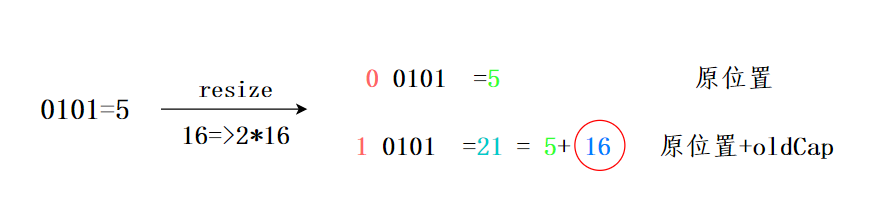
Nói cách khác, theo thuật toán băm mới của JDK 8, vị trí chỉ mục sau khi mảng được mở rộng là vị trí chỉ mục gốc hoặc "chỉ mục gốc + dung lượng gốc", tuân theo các quy tắc nhất định.

Tất nhiên, công lao này thuộc về cả thuật toán băm mới và tiền đề rằng n là lũy thừa nguyên của 2. Đây là kết quả của những nỗ lực chung của họ hash & (newCapacity - 1).

Tóm tắt

Khi thêm các phần tử vào HashMap, nếu số lượng phần tử vượt qua giới hạn được xác định bởi tích của hệ số tải (load factor) và độ dài của mảng, HashMap sẽ thực hiện thao tác mở rộng tự động để đảm bảo rằng không có quá nhiều phần tử trong bộ nhớ.

Quá trình mở rộng của HashMap

Điều kiện mở rộng: Khi số lượng phần tử vượt quá load factor nhân với độ dài mảng, HashMap sẽ mở rộng mảng lên gấp đôi.
Bước mở rộng:
- HashMap tạo một mảng mới có độ dài gấp đôi so với mảng hiện tại.
- Tất cả các phần tử từ mảng cũ được tái phân bố vào mảng mới dựa trên giá trị hash của key và độ dài mới của mảng.
Phân bố phần tử:
- Mỗi phần tử được xác định vị trí mới trong mảng mới bằng cách sử dụng phép toán hash & (newCapacity - 1), với newCapacity là độ dài mới của mảng.
- Phần lớn các phần tử vẫn giữ nguyên vị trí, nhưng một số phần tử sẽ di chuyển đến các vị trí mới được tính bằng "vị trí cũ + độ dài cũ của mảng".

03. Tại sao hệ số tải lại là 0,75?

Trong câu hỏi trước đó đã đề cập đến hệ số tải (hay còn gọi là hệ số tải), vậy câu hỏi này chúng ta sẽ thảo luận tại sao hệ số tải lại là 0.75 mà không phải là 0.6, 0.8.

Chúng ta biết rằng, HashMap được thực hiện bằng cách sử dụng mảng kết hợp với danh sách liên kết / cây đỏ đen, để thêm dữ liệu (phần tử/ cặp khóa giá trị) vào HashMap hoặc lấy dữ liệu từ đó, chúng ta cần xác định chỉ số (chỉ mục) của dữ liệu trong mảng.

Đầu tiên, chúng ta sẽ băm khóa dữ liệu một lần:

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

Tiếp theo, chúng ta sẽ thực hiện phép toán lấy dư để xác định chỉ số:

i = (n - 1) & hash

Quá trình này có thể dẫn đến hai vấn đề:

Kích thước của mảng quá nhỏ, sau khi tính toán băm, chỉ số dễ gây ra xung đột.
Kích thước của mảng quá lớn, dẫn đến không tận dụng tốt không gian.

Hệ số tải được sử dụng để biểu thị mức độ lấp đầy dữ liệu trong HashMap:

Hệ số tải = Số lượng dữ liệu đã điền vào bảng băm / Độ dài của bảng băm

Điều này có nghĩa là:

Hệ số tải càng nhỏ, số lượng dữ liệu điền vào càng ít, nguy cơ xung đột băm càng giảm, nhưng đồng thời lãng phí không gian và tăng khả năng kích hoạt quá trình mở rộng.
Hệ số tải càng lớn, số lượng dữ liệu điền vào càng nhiều, tận dụng không gian càng tốt, nhưng nguy cơ xung đột băm càng cao.

Thật khó khăn! ! ! !

Điều này đòi hỏi chúng ta phải cân bằng giữa "xung đột băm" và "tận dụng không gian", cố gắng duy trì sự cân bằng, không làm ảnh hưởng đến nhau.

Chúng ta biết rằng, HashMap giải quyết xung đột băm bằng phương pháp xích đu (chaining).

Để giảm thiểu khả năng xảy ra xung đột băm, khi độ dài mảng của HashMap đạt đến một "giá trị ngưỡng" nào đó, quá trình mở rộng sẽ được kích hoạt. Sau khi mở rộng, các phần tử từ mảng nhỏ trước đó sẽ được chuyển sang mảng lớn hơn, đây là một hoạt động tốn thời gian.

Giá trị ngưỡng này được xác định bởi điều gì?

Giá trị ngưỡng = Dung lượng ban đầu * Hệ số tải

Ban đầu, dung lượng của HashMap là 16:

static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // tương đương với 16

Hệ số tải là 0.75:

static final float DEFAULT_LOAD_FACTOR = 0.75f;

Điều này có nghĩa là, khi 16 * 0.75 = 12, quá trình mở rộng sẽ được kích hoạt.

Tại sao lại chọn hệ số tải là 0.75? Tại sao không phải là 0.8, 0.6?

Điều này liên quan đến một nguyên lý quan trọng trong thống kê - phân phối Poisson.

Đã đến lúc tham khảo Wikipedia:

Phân phối Poisson là một phân phối xác suất rời rạc phổ biến trong thống kê và xác suất học, được nhà toán học người Pháp Simeon-Denis Poisson đề xuất vào năm 1838. Nó mô hình hoá số lần xảy ra của một sự kiện ngẫu nhiên trong một khoảng thời gian, khoảng cách, diện tích, v.v.

Giáo sư Ruan Yi Phong từng chi tiết giới thiệu phân phối Poisson và phân phối mũ, mọi người có thể xem qua.

Liên kết: https://www.ruanyifeng.com/blog/2015/06/poisson-distribution.html

Cụ thể, nó được biểu diễn bằng một công thức như vậy.

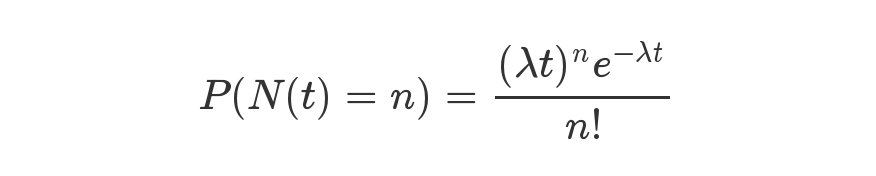
Trong tài liệu doc của HashMap có mô tả như sau:

Because TreeNodes are about twice the size of regular nodes, we
use them only when bins contain enough nodes to warrant use
(see TREEIFY_THRESHOLD). And when they become too small (due to
removal or resizing) they are converted back to plain bins.  In
usages with well-distributed user hashCodes, tree bins are
rarely used.  Ideally, under random hashCodes, the frequency of
nodes in bins follows a Poisson distribution
(http://en.wikipedia.org/wiki/Poisson_distribution) with a
parameter of about 0.5 on average for the default resizing
threshold of 0.75, although with a large variance because of
resizing granularity. Ignoring variance, the expected
occurrences of list size k are (exp(-0.5) * pow(0.5, k) /
factorial(k)). The first values are:
0:    0.60653066
1:    0.30326533
2:    0.07581633
3:    0.01263606
4:    0.00157952
5:    0.00015795
6:    0.00001316
7:    0.00000094
8:    0.00000006
more: less than 1 in ten million

Để mọi người dễ hiểu, chúng ta cùng xem lại phương pháp zip và cấu trúc cây đỏ đen của HashMap.

Trước Java 8, HashMap đã sử dụng danh sách liên kết để giải quyết xung đột, nghĩa là khi hai hoặc nhiều khóa được ánh xạ vào cùng một nhóm, chúng sẽ được đặt vào danh sách liên kết của cùng một nhóm. Khi có quá nhiều nút (Node) trong danh sách liên kết, danh sách liên kết sẽ trở nên rất dài và hiệu quả tìm kiếm (Hiệu quả tìm kiếm là O(n)) sẽ bị ảnh hưởng.

Trong Java 8, khi số lượng nút trong danh sách liên kết vượt quá ngưỡng (8), danh sách liên kết sẽ được chuyển đổi thành cây đỏ đen (nút là TreeNode) và cây đỏ đen (khi nói về TreeMap là một cấu trúc cây cân bằng hiệu quả có thể hoàn thành các thao tác chèn, xóa và tìm kiếm trong thời gian O(log n). Cấu trúc này có thể cải thiện hiệu suất và khả năng mở rộng của HashMap khi số lượng nút lớn.

Mặc dù mục đích ban đầu của đoạn này là để trình bày lý do tại sao việc chuyển đổi cây đỏ-đen được thực hiện khi chiều dài dây kéo vượt quá 8 trong jdk 8, hệ số tải 0,75 được đề cập nhưng lý do không được đề cập.

Để tìm hiểu lý do tại sao, tôi đã xem qua bài viết này:

Link tham khảo: https://segmentfault.com/a/1190000023308658

Một khái niệm được đề cập: Phân phối nhị thức.

Khi làm một việc gì đó, chỉ có hai khả năng xảy ra kết quả, giống như việc tung đồng xu, mặt ngửa hoặc mặt sấp.

Nếu chúng ta thực hiện N thí nghiệm thì mỗi thí nghiệm chỉ có hai kết quả có thể xảy ra và mỗi thí nghiệm là độc lập, các thí nghiệm khác nhau không ảnh hưởng lẫn nhau và xác suất thành công của mỗi thí nghiệm là như nhau.

Dựa trên lý thuyết này: chúng ta ném dữ liệu vào bảng băm và nếu xảy ra xung đột băm thì là thất bại, ngược lại là thành công.

Chúng ta có thể tưởng tượng rằng giá trị băm của thử nghiệm là ngẫu nhiên và các khóa đã được băm sẽ được ánh xạ tới không gian địa chỉ của bảng băm nên kết quả cũng là ngẫu nhiên. Vì vậy, mỗi lần chúng ta đặt, nó tương đương với việc ném một con xúc xắc 16 mặt (độ dài mặc định của mảng sau lần mở rộng đầu tiên của HashMap là 16). Khi va chạm xảy ra, các số lặp lại xuất hiện sau khi bị ném n lần.

Vậy mục đích của chúng ta là gì?

Có nghĩa là sau khi tung xúc xắc k lần, không có viên nào có xác suất bằng nhau. Nói chung, chúng ta phải lớn hơn 0,5 (con số này là một con số lý tưởng).

Do đó, xác suất va chạm là 0 trong số n sự kiện được tính từ công thức trên:

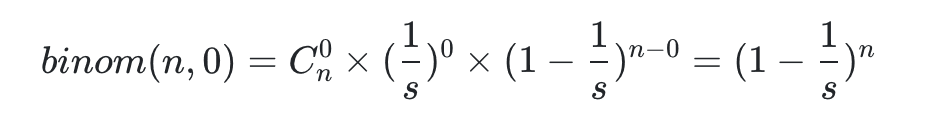
Giá trị xác suất này cần phải lớn hơn 0,5. Chúng tôi tin rằng sơ đồ băm như vậy có thể mang lại tỷ lệ xung đột rất thấp. Vì thế:

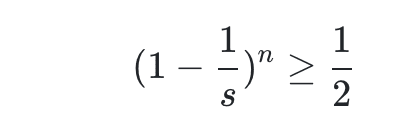
Lúc này, điều chúng ta mong muốn nhất đối với công thức này là khi độ dài n phải được mở rộng bao nhiêu lần? Hệ số tải là $N/S$ giá trị. Vì vậy, đạo hàm như sau:

Vì vậy bạn có thể nhận được

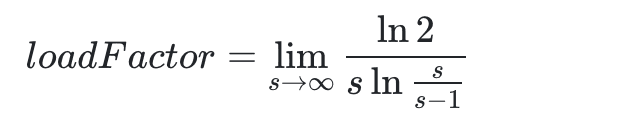
TRONG

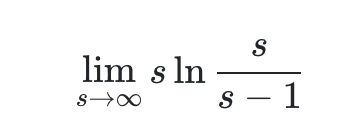
Đây là bài toán tìm giới hạn ∞⋅0 của hàm số hàm số $s = m+1（m \to \infty）$

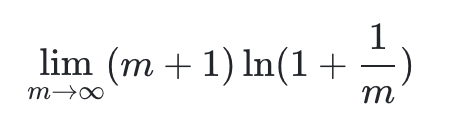
Chúng tôi đặt $x = \frac{1}{m} （x \to 0）$ sau đó có:

Vì thế:

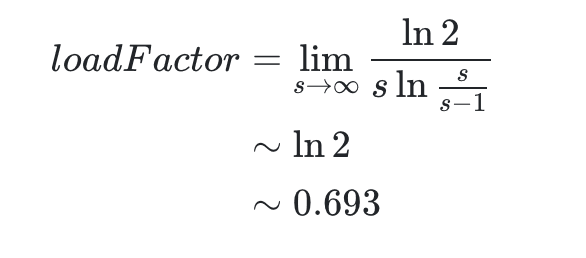
Có một yêu cầu khi xem xét dung lượng của HashMap: nó phải là lũy thừa n của 2. Khi hệ số tải được chọn là 0,75, có thể đảm bảo rằng tích của nó nhân với công suất là một số nguyên.

16*0.75=12
32*0.75=24

Ngoài 0,75, còn có 0,625 (5/8) và 0,875 (7/8) nằm trong khoảng từ 0,5 đến 1. Từ góc độ trung vị, 0,75 là hoàn hảo hơn. Ngoài ra, Wikipedia nói rằng hệ số tải của phương pháp chaining (một phương pháp giải quyết xung đột băm) tốt nhất nên được giới hạn ở mức dưới 0,7-0,8. Nếu vượt quá 0,8, bộ đệm CPU bị thiếu trong quá trình tra cứu bảng sẽ tăng theo đường cong hàm mũ.

Tóm lại, 0,75 là một lựa chọn hoàn hảo.

Tóm tắt

Hệ số tải (load factor) của HashMap là tỷ lệ giữa số lượng phần tử đã được thêm vào và số lượng bucket trong bảng băm. Khi số lượng phần tử đạt đến tích của hệ số tải và số lượng bucket, HashMap sẽ thực hiện thao tác mở rộng. Thông thường, giá trị hệ số tải được chọn là 0.75. Lựa chọn này dựa trên việc cân nhắc giữa chi phí thời gian và chi phí không gian, giúp đảm bảo hiệu suất của HashMap đạt được mức đáng kể.

Hệ số tải quá cao: Nếu hệ số tải quá cao, tức là số lượng phần tử thêm vào quá nhiều, các phần tử trong HashMap sẽ tập trung vào ít bucket hơn, dẫn đến tăng số lượng xung đột. Điều này làm giảm hiệu suất các thao tác tìm kiếm, thêm và xóa, đồng thời yêu cầu phải thực hiện thao tác mở rộng thường xuyên hơn, làm giảm hiệu năng.
Hệ số tải quá thấp: Ngược lại, nếu hệ số tải được đặt quá thấp, số lượng bucket sẽ tăng lên, mặc dù có thể giảm xung đột, nhưng cũng có thể làm lãng phí không gian. Do đó, việc chọn hệ số tải là 0.75 giúp đạt được sự cân bằng tốt giữa hiệu suất và sử dụng không gian.

Tóm lại, lựa chọn giá trị 0.75 cho hệ số tải giúp đạt được sự cân bằng tối ưu giữa thời gian và không gian cho HashMap, từ đó tối ưu hóa hiệu suất của nó.

04. Vấn đề an toàn đa luồng

Vấn đề này không cần nói quá nhiều, nhưng có thể một vài nhà phỏng vấn sẽ hỏi như đã đề cập ở đây, vì vậy đơn giản tôi sẽ giải thích một chút.

Có ba nguyên nhân chính:

Đa luồng khi mở rộng có thể dẫn đến vòng lặp vô hạn.
Đa luồng khi thêm phần tử có thể dẫn đến mất mát các phần tử.
Các hoạt động đồng thời của put và get có thể dẫn đến việc get được giá trị null.

1) Đa luồng khi mở rộng có thể dẫn đến vòng lặp vô hạn

Như chúng ta biết, HashMap sử dụng phương pháp chuỗi liên kết để giải quyết xung đột băm, nghĩa là khi có xung đột băm, các cặp khóa-giá trị với cùng giá trị băm sẽ được lưu trữ dưới dạng chuỗi liên kết.

Trong JDK 7, nó sử dụng phương pháp chèn vào đầu để lưu trữ chuỗi, nghĩa là các cặp khóa-giá trị xung đột sẽ được chèn vào trước cặp khóa-giá trị trước đó trong chuỗi (đã đề cập khi thảo luận về mở rộng). Việc mở rộng có thể dẫn đến hình thành chuỗi vòng, gây ra vòng lặp vô hạn.

Mã nguồn của phương thức resize:

// newCapacity là dung lượng mới
void resize(int newCapacity) {
    // oldTable là bảng cũ
    Entry[] oldTable = table;
    // oldCapacity là dung lượng cũ
    int oldCapacity = oldTable.length;
    // MAXIMUM_CAPACITY là dung lượng lớn nhất, 2 mũ 30 = 1<<30
    if (oldCapacity == MAXIMUM_CAPACITY) {
        // Điều chỉnh dung lượng thành giá trị tối đa của Integer 0x7fffffff (hệ 16) = 2^31-1
        threshold = Integer.MAX_VALUE;
        return;
    }

    // Khởi tạo một mảng mới (dung lượng lớn)
    Entry[] newTable = new Entry[newCapacity];
    // Chuyển dữ liệu từ mảng cũ sang mảng mới
    transfer(newTable, initHashSeedAsNeeded(newCapacity));
    // Tham chiếu đến mảng mới
    table = newTable;
    // Tính toán lại ngưỡng
    threshold = (int)Math.min(newCapacity * loadFactor, MAXIMUM_CAPACITY + 1);
}

Phương thức transfer để chuyển dữ liệu, sao chép các phần tử từ mảng cũ sang mảng mới.

void transfer(Entry[] newTable, boolean rehash) {
    // newCapacity là dung lượng mới
    int newCapacity = newTable.length;
    // Duyệt qua mảng cũ
    for (Entry<K,V> e : table) {
        while(null != e) {
            // Phương pháp chuỗi liên kết, giá trị khóa khác nhau trên cùng một key
            Entry<K,V> next = e.next;
            // Cần phải tính lại hash
            if (rehash) {
                e.hash = null == e.key ? 0 : hash(e.key);
            }
            // Tính toán chỉ số của mảng dựa trên dung lượng lớn và hash key của phần tử
            int i = indexFor(e.hash, newCapacity);

            // Phần tử mới được chèn vào đầu danh sách
            e.next = newTable[i];

            // Chèn vào mảng mới
            newTable[i] = e;

            // Phần tử tiếp theo trong danh sách
            e = next;
        }
    }
}

Chú ý đến các dòng e.next = newTable[i] và newTable[i] = e, hai dòng code này sẽ đặt phần tử mới vào đầu danh sách liên kết.

Nó trông như thế nào trước khi mở rộng như sau.

Sau đó, sau khi mở rộng bình thường, nó sẽ trông như thế này.

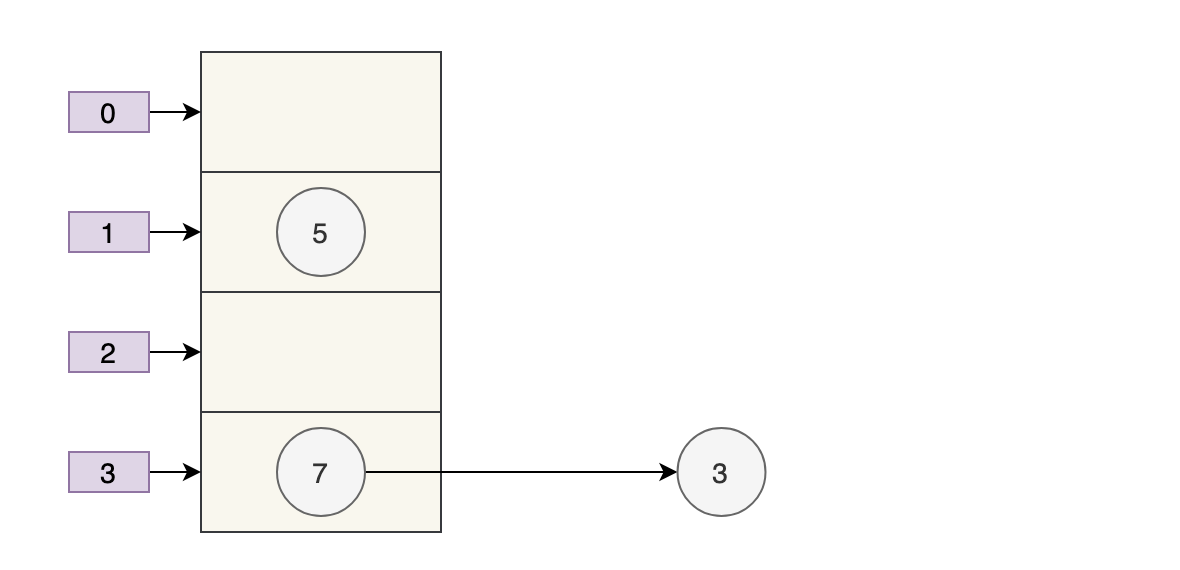
Giả sử rằng có hai luồng mở rộng cùng một lúc. Thread A newTable[i] = e;bị treo khi thực thi. Tại thời điểm này, Thread A: e=3, next=7, e.next=null.

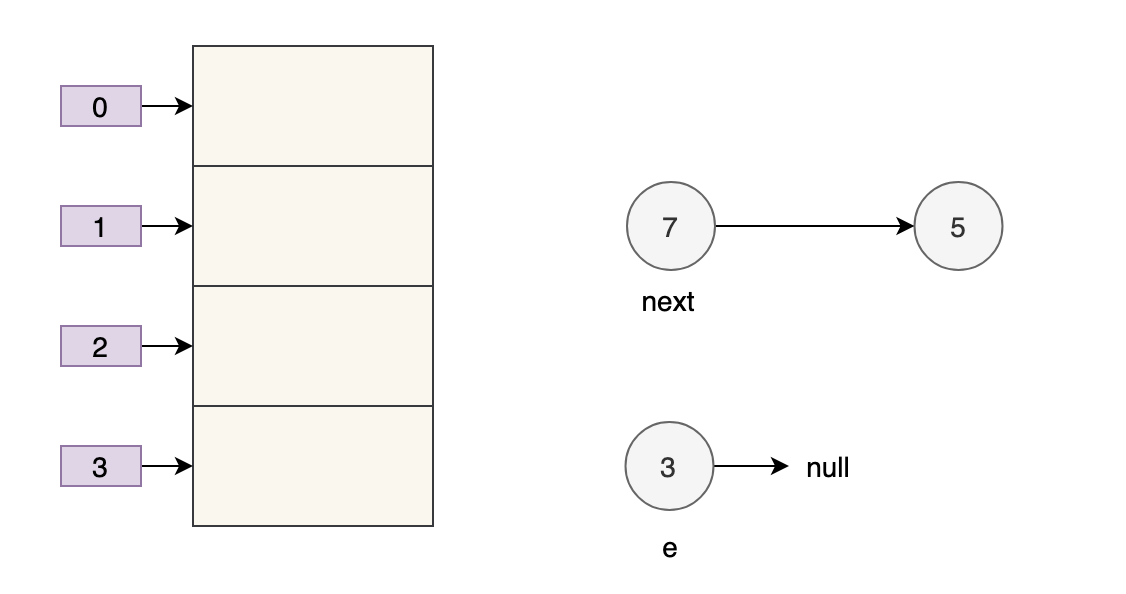
Thread B bắt đầu thực thi và hoàn thành việc truyền dữ liệu.

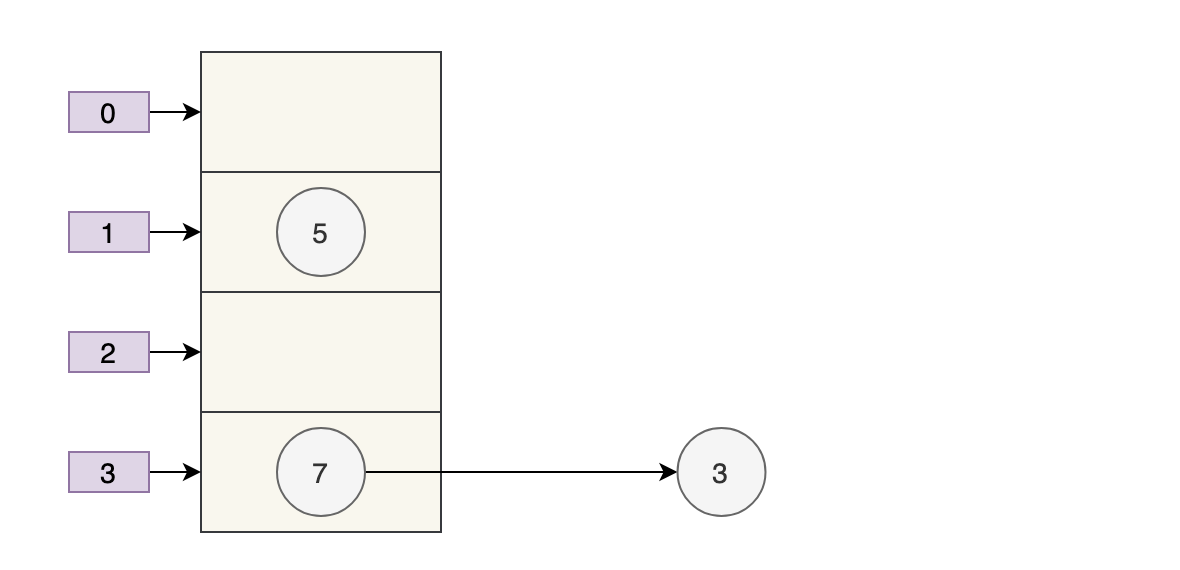
Tại thời điểm này, số tiếp theo của 7 là 3 và số tiếp theo của 3 là null.

Sau đó, luồng A lấy time slice CPU để tiếp tục thực thi newTable[i] = evà đặt 3 vào vị trí tương ứng của mảng mới. Sau khi thực hiện chu trình này, tình huống của luồng A như sau:

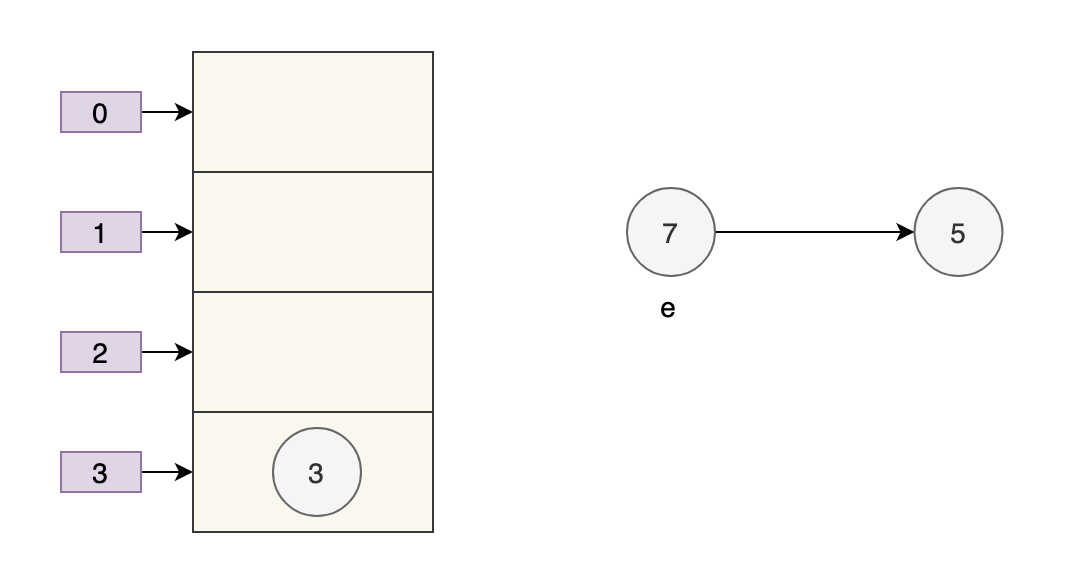
Thực hiện vòng lặp tiếp theo, tại thời điểm này e=7, ban đầu số tiếp theo trong số 7 trong luồng A là 5, nhưng vì bảng được chia sẻ bởi luồng A và luồng B và sau khi luồng B được thực thi thành công, số tiếp theo của 7 trở thành 3, sau đó trong luồng A, số tiếp theo của 7 cũng là 3.

Sử dụng phương pháp chèn đầu, nó sẽ như thế này:

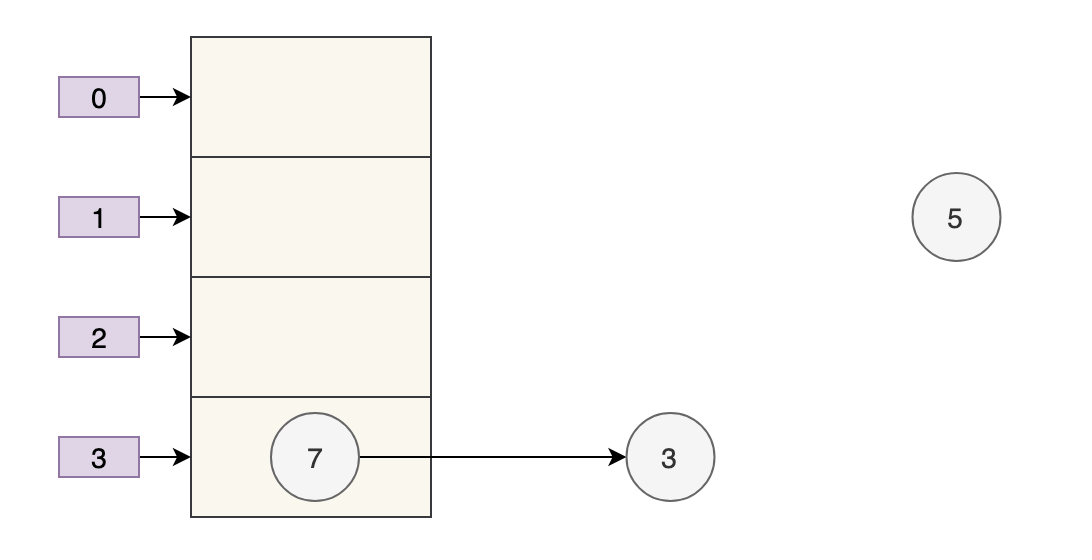
Có vẻ như không có vấn đề gì, lúc này next = 3, e = 3.

Vòng lặp tiếp theo được thực hiện, nhưng tại thời điểm này, vì luồng B thay đổi số 3 tiếp theo thành null, nên vòng lặp này phải là vòng cuối cùng.

Tiếp theo, khi quá trình thực thi hoàn tất e.next=newTable[i], tức là 3.next=7, 3 và 7 được liên kết với nhau. newTable[i]=eSau khi thực hiện, 3 được chèn lại vào danh sách liên kết bằng phép nội suy đầu. hình dưới đây:

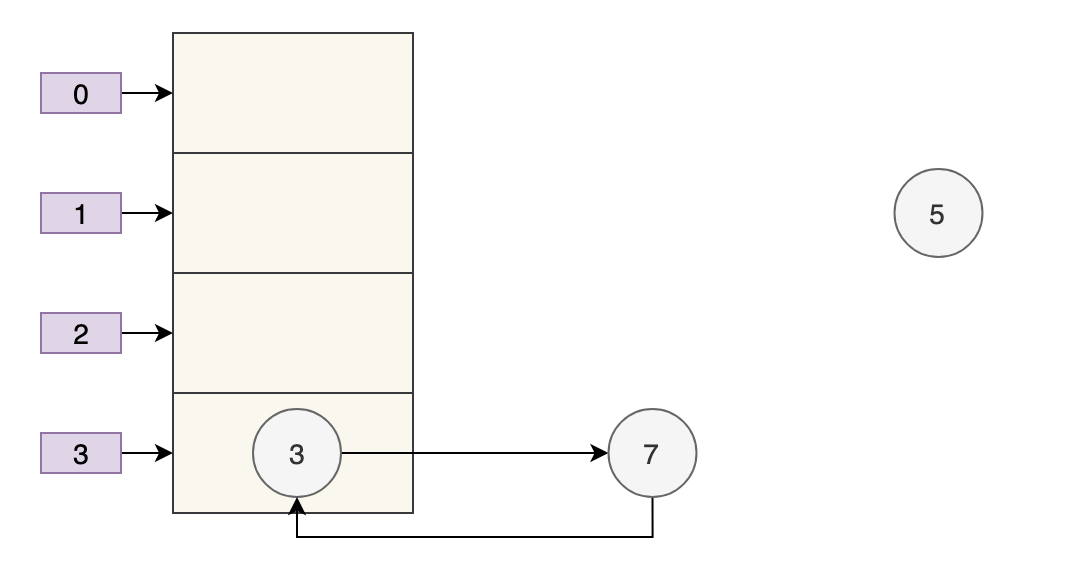
Bắt đầu từ búp bê matryoshka, Element 5 đã trở thành một đứa bé bị bỏ rơi, khốn khổ~~~

Tuy nhiên, vấn đề này đã được khắc phục trong JDK 8, và thứ tự ban đầu của danh sách liên kết sẽ được giữ nguyên trong quá trình mở rộng (à, giống như nói lâu vô ích vậy, haha, câu hỏi phỏng vấn này đúng là như thế này, rất là hay) chảy nước miếng, nhưng một số người phỏng vấn thực sự là lực lượng kiêu ngạo).

2) Khi put ở chế độ đa luồng sẽ khiến các phần tử bị mất

Thông thường, khi xảy ra xung đột băm, HashMap trông như thế này:

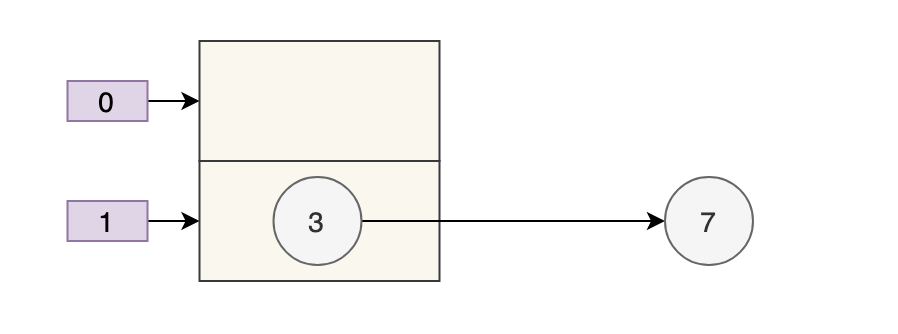
Tuy nhiên, khi có nhiều luồng đồng thời thực hiện thao tác put, nếu vị trí chỉ mục tính toán được là giống nhau, điều này sẽ dẫn đến khóa key trước bị ghi đè bởi key sau, dẫn đến mất mát phần tử.

Mã nguồn put:

final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
               boolean evict) {
    Node<K,V>[] tab; Node<K,V> p; int n, i;

    // Bước ①: Tạo bảng nếu chưa tồn tại
    if ((tab = table) == null || (n = tab.length) == 0)
        n = (tab = resize()).length;

    // Bước ②: Tính toán chỉ mục và xử lý khi giá trị là null
    if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null);
    else {
        Node<K,V> e; K k;

        // Bước ③: Key của nút đã tồn tại, chỉ cần ghi đè giá trị
        if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k))))
            e = p;

        // Bước ④: Kiểm tra nếu danh sách này là cây đỏ đen
        else if (p instanceof TreeNode)
            e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);

        // Bước ⑤: Danh sách này là danh sách liên kết
        else {
            for (int binCount = 0; ; ++binCount) {
                if ((e = p.next) == null) {
                    p.next = newNode(hash, key, value, null);

                    // Nếu chiều dài danh sách lớn hơn 8, chuyển thành cây đỏ đen để xử lý
                    if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                        treeifyBin(tab, hash);
                    break;
                }

                // Key đã tồn tại, chỉ cần ghi đè giá trị
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    break;
                p = e;
            }
        }

        // Bước ⑥: Ghi đè trực tiếp
        if (e != null) { // existing mapping for key
            V oldValue = e.value;
            if (!onlyIfAbsent || oldValue == null)
                e.value = value;
            afterNodeAccess(e);
            return oldValue;
        }
    }
    ++modCount;

    // Bước ⑦: Thay đổi kích thước bảng nếu vượt quá dung lượng tối đa
    if (++size > threshold)
        resize();
    afterNodeInsertion(evict);
    return null;
}

Vấn đề xảy ra tại Bước ②:

if ((p = tab[i = (n - 1) & hash]) == null)
    tab[i] = newNode(hash, key, value, null);

Hai luồng đều thực hiện câu lệnh if, giả sử luồng A thực hiện tab[i] = newNode(hash, key, value, null) trước, bảng table sẽ như sau:

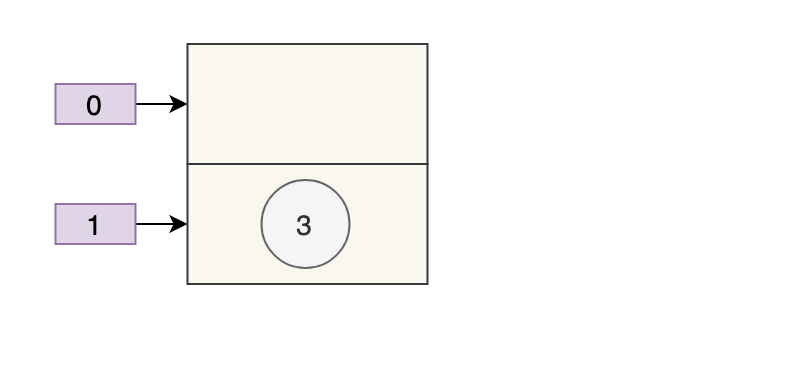
Tiếp theo, luồng B thực hiện tab[i] = newNode(hash, key, value, null), bảng table sẽ như sau:

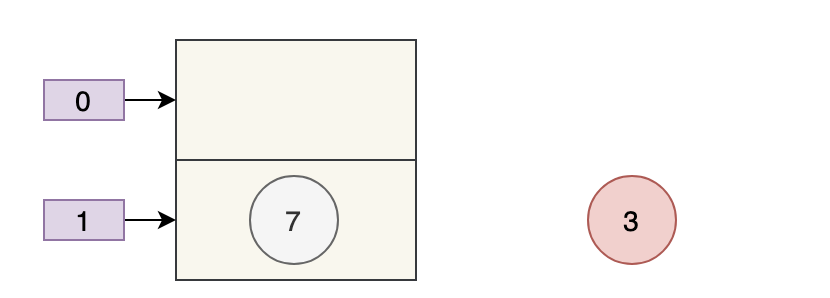
Điều này dẫn đến mất mát dữ liệu của phần tử 3.

3) Khi thực hiện đồng thời các thao tác put và get có thể dẫn đến việc get được giá trị null

Khi Thread 1 thực hiện thao tác put, và do số lượng phần tử vượt quá ngưỡng nên gây ra việc phải mở rộng bảng, lúc này Thread 2 đang thực hiện thao tác get, có thể gặp phải vấn đề này.

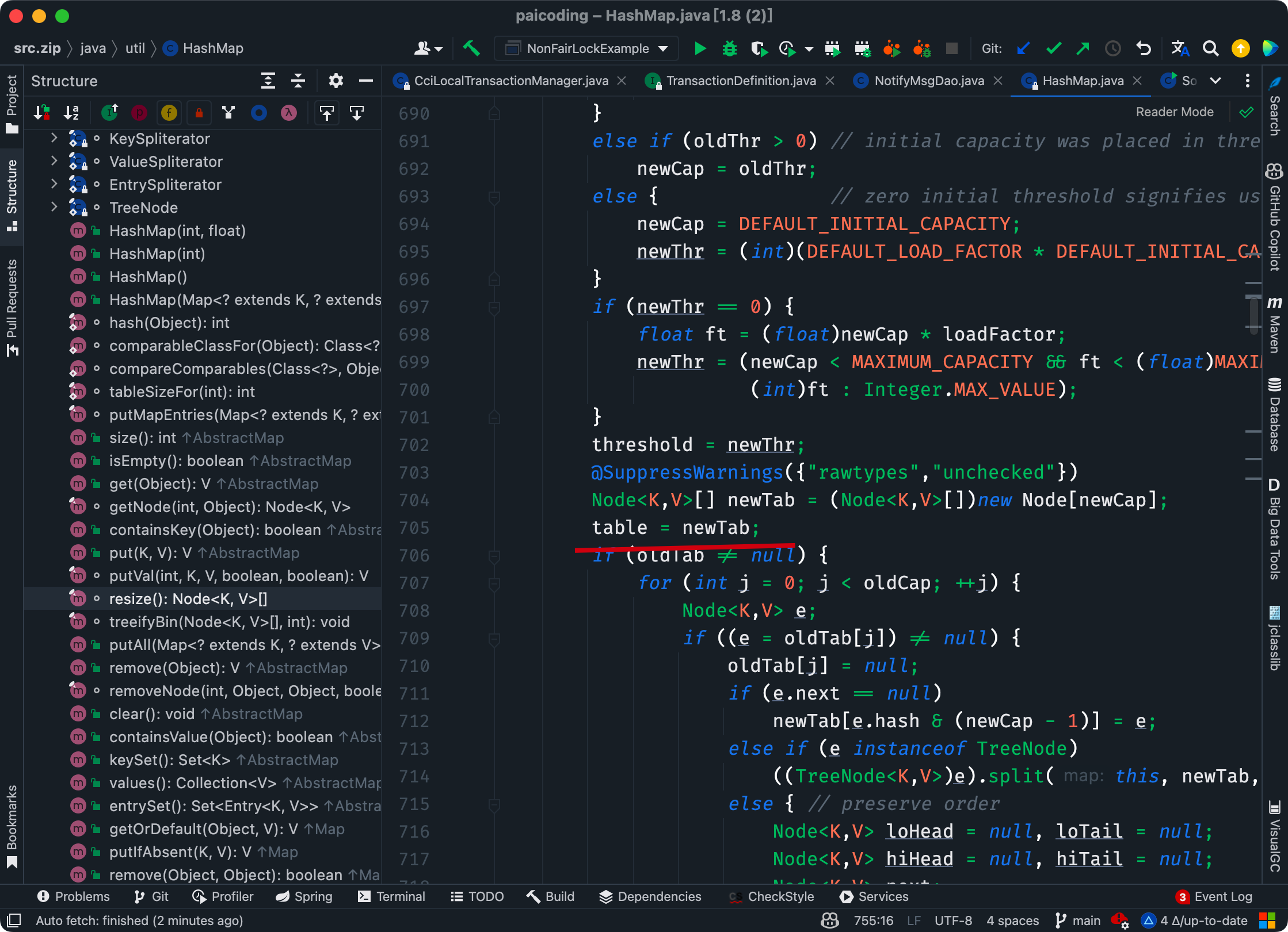
Khi thực hiện mở rộng bảng, sau khi Thread 1 thực hiện table = newTab, bảng table trong Thread 2 cũng được cập nhật, nhưng lúc này dữ liệu vẫn chưa hoàn toàn chuyển đổi. Vì vậy, nếu Thread 2 đang thực hiện thao tác get, có thể nó sẽ không tìm thấy phần tử trong bảng cũ và trả về giá trị null.

4) Tóm tắt

HashMap không an toàn đối với luồng chủ yếu là do trong quá trình thêm, xóa và mở rộng, có thể làm thay đổi cấu trúc của danh sách liên kết và từ đó làm hỏng tính bất biến của HashMap. Cụ thể, nếu một luồng đang duyệt qua danh sách liên kết của HashMap và một luồng khác tại thời điểm đó thay đổi danh sách này (ví dụ thêm một nút), sẽ dẫn đến thay đổi cấu trúc của danh sách và ảnh hưởng đến việc duyệt của luồng đang thực hiện, có thể dẫn đến việc duyệt không thành công hoặc vòng lặp vô hạn và các vấn đề khác.

Để giải quyết vấn đề này, Java cung cấp lớp ConcurrentHashMap làm cho HashMap trở thành an toàn cho các luồng. ConcurrentHashMap sử dụng khóa phân đoạn (Segment) nội bộ, chia toàn bộ Map thành nhiều HashMap nhỏ. Mỗi HashMap nhỏ có khóa riêng của nó, cho phép các luồng khác nhau truy cập các phần khác nhau của Map cùng một lúc mà không ảnh hưởng đến các phần khác. Khi thực hiện các thao tác thêm, xóa và mở rộng, chỉ cần khóa từng HashMap nhỏ, không cần khóa toàn bộ ConcurrentHashMap, từ đó cải thiện hiệu suất và độ bền trong môi trường đa luồng.

Tóm lại, để sử dụng bảng băm an toàn cho các luồng, nên sử dụng ConcurrentHashMap hoặc sử dụng đồng bộ hóa tường minh để đảm bảo an toàn cho các luồng.

05. Tóm tắt

HashMap là một trong những cấu trúc dữ liệu phổ biến nhất trong Java, nó là một cấu trúc lưu trữ các cặp khóa - giá trị và cho phép truy cập nhanh vào giá trị dựa trên khóa. Dưới đây là tổng kết về HashMap:

HashMap sử dụng cấu trúc lưu trữ mảng kết hợp với danh sách liên kết hoặc cây đỏ đen, cho phép thực hiện các thao tác thêm, xóa, tìm kiếm với độ phức tạp O(1).
HashMap không an toàn đối với các luồng (non-thread-safe), do đó trong môi trường đa luồng cần sử dụng ConcurrentHashMap để đảm bảo an toàn.
Cơ chế mở rộng của HashMap thực hiện bằng cách tăng kích thước mảng và tính lại giá trị hash, dẫn đến việc mở rộng có thể ảnh hưởng đến hiệu suất khi có nhiều phần tử.
Từ Java 8, HashMap sử dụng phương pháp nén danh sách và cây để tối ưu hóa việc lưu trữ một lượng lớn phần tử, cải thiện hiệu suất.
Key trong HashMap là duy nhất, nếu cố gắng lưu trữ key trùng lặp, giá trị sau sẽ ghi đè giá trị trước.
Bạn có thể thiết lập kích thước ban đầu và hệ số tải của HashMap, kích thước ban đầu chỉ ra kích thước ban đầu của mảng, hệ số tải chỉ ra tỷ lệ mà mảng sẽ được điền. Nói chung, kích thước ban đầu là 16, hệ số tải là 0.75.
Khi duyệt HashMap, nó không có thứ tự, vì vậy nếu bạn cần duyệt theo thứ tự, bạn nên sử dụng TreeMap.

Tóm lại, HashMap là một cấu trúc dữ liệu hiệu quả với khả năng tìm kiếm và chèn nhanh chóng, nhưng cần chú ý đến vấn đề an toàn đối với các luồng và hiệu suất.