Algorithm Complexity

Độ phức tạp của thuật toán

1. Giới thiệu về độ phức tạp của thuật toán

Độ phức tạp của thuật toán (Algorithm complexity): Là cách sử dụng thời gian và không gian của chương trình trong điều kiện đầu vào của vấn đề có kích thước là $n$ .

Mục đích của "phân tích thuật toán" là cải tiến thuật toán. Như đã đề cập ở trên: Mục tiêu của thuật toán là tối ưu hóa thời gian chạy (Độ phức tạp thời gian thấp hơn) và không gian sử dụng (không gian phức tạp thấp hơn). Vì vậy, việc thực hiện "phân tích thuật toán" là phân tích thuật toán từ hai khía cạnh sử dụng thời gian và sử dụng không gian.

So sánh sự ưu và nhược điểm của hai thuật toán thường có hai phương pháp:

Thống kê sau khi thực hiện: Viết hai chương trình thực thi cho hai thuật toán, ghi lại thời gian chạy và kích thước không gian sử dụng thực tế của mỗi thuật toán, sau đó chọn thuật toán tốt nhất.
Ước tính trước: Sau khi thiết kế thuật toán, dựa trên các bước trong thuật toán, ước tính thời gian chạy và không gian sử dụng của thuật toán. So sánh giá trị ước tính của hai thuật toán và chọn thuật toán tốt nhất.

Trong hầu hết các trường hợp, chúng ta sẽ chọn phương pháp thứ hai. Vì công việc của phương pháp thứ nhất quá lớn và không đáng kể. Ngoài ra, ngay cả khi cùng một thuật toán được thực hiện bằng các ngôn ngữ khác nhau, trên các máy tính khác nhau, thời gian chạy cũng không giống nhau. Vì vậy, chúng ta thường sử dụng phương pháp ước tính trước để đánh giá thuật toán.

Trong phương pháp ước tính trước, ngôn ngữ biên dịch và tốc độ chạy máy tính không phải là những yếu tố chúng ta quan tâm. Chúng ta chỉ quan tâm đến việc tăng kích thước của vấn đề $n$ , thời gian và không gian sử dụng tương ứng cũng tăng theo cách nào.

Ở đây, "kích thước vấn đề $n$ " có nghĩa là: số lượng dữ liệu đầu vào của vấn đề thuật toán. Định nghĩa cũng không giống nhau cho các thuật toán khác nhau.

Trong thuật toán sắp xếp: $n$ đại diện cho số lượng phần tử cần sắp xếp.
Trong thuật toán tìm kiếm: $n$ đại diện cho tổng số phần tử trong phạm vi tìm kiếm: ví dụ như kích thước mảng, kích thước ma trận 2D, độ dài chuỗi, số lượng nút trong cây nhị phân, số lượng nút và cạnh trong đồ thị, v.v.
Trong thuật toán liên quan đến tính toán nhị phân: $n$ đại diện cho chiều rộng của biểu diễn nhị phân.

Nói chung, kích thước của vấn đề càng gần nhau, chi phí tính toán tương ứng cũng càng gần nhau. Và khi kích thước của vấn đề mở rộng, chi phí tính toán cũng tăng theo xu hướng tăng. Tiếp theo, chúng ta sẽ giải thích cụ thể về "độ phức tạp thời gian" và "độ phức tạp không gian".

2. Độ phức tạp thời gian

2.1 Giới thiệu về độ phức tạp thời gian

Độ phức tạp thời gian (Time Complexity): Là thời gian mà thuật toán cần để chạy trong điều kiện đầu vào của vấn đề có kích thước là $n$ , có thể được ký hiệu là $T(n)$ .

Chúng ta sử dụng số lần thực hiện các thao tác cơ bản làm đơn vị đo lường cho độ phức tạp thời gian. Nói cách khác, độ phức tạp thời gian tương quan với số lần thực hiện các thao tác cơ bản trong thuật toán.

Thao tác cơ bản: Mỗi câu lệnh trong thuật toán. Mỗi thao tác cơ bản có thể hoàn thành trong thời gian hằng số.

Thao tác cơ bản là một thao tác mà thời gian thực hiện không phụ thuộc vào số lượng phần tử của dữ liệu đầu vào.

Ví dụ, thao tác cộng hai số nguyên là một thao tác cơ bản. Nếu kích thước của hai số không lớn, thời gian thực hiện không phụ thuộc vào số lượng chữ số của số nguyên, vì vậy thao tác cộng có thể coi là một thao tác cơ bản.

Ngược lại, nếu kích thước của hai số rất lớn, thao tác cộng phụ thuộc vào số lượng chữ số của hai số, do đó thao tác cộng hai số không phải là một thao tác cơ bản, mà mỗi thao tác cộng một chữ số mới là một thao tác cơ bản.

Dưới đây là một ví dụ cụ thể để giải thích cách tính độ phức tạp thời gian.

def algorithm(n):
    fact = 1
    for i in range(1, n + 1):
        fact *= i
    return fact

Tổng số lần thực hiện các câu lệnh trong thuật toán trên là $1 + n + n + 1 = 2n + 2$ , có thể sử dụng hàm $f(n)$ để biểu thị số lần thực hiện các câu lệnh: $f(n) = 2n + 2$ .

Do đó, hàm độ phức tạp thời gian có thể được biểu thị là: $T(n) = O(f(n))$ . Nó biểu thị xu hướng tăng của thời gian thực hiện thuật toán khi kích thước của vấn đề $n$ tăng lên. $O$ là một ký hiệu tiệm cận, $T(n)$ được gọi là độ phức tạp thời gian tiệm cận (Asymptotic Time Complexity), viết tắt là độ phức tạp thời gian.

Khái niệm "xu hướng tăng của thời gian thực hiện thuật toán" là một khái niệm mơ hồ, thường chúng ta sử dụng các ký hiệu như $O$ để biểu thị độ phức tạp thời gian.

2.2 Ký hiệu tiệm cận

Ký hiệu tiệm cận (Asymptotic Symbol): Được sử dụng để mô tả tốc độ tăng của một hàm. Đơn giản nói, ký hiệu tiệm cận chỉ giữ lại bậc cao nhất của hàm, bỏ qua các phần tăng trưởng chậm hơn của hàm, chẳng hạn như bậc thấp, hệ số, hằng số. Vì khi kích thước của vấn đề trở nên rất lớn, các phần này không ảnh hưởng đến xu hướng tăng, nên có thể bỏ qua.

Có ba ký hiệu tiệm cận thường được sử dụng: Ký hiệu tiệm cận chặt chẽ $\Theta$ , ký hiệu tiệm cận trên $O$ , ký hiệu tiệm cận dưới $\Omega$ 。Tiếp theo chúng ta sẽ giải thích từng ký hiệu.

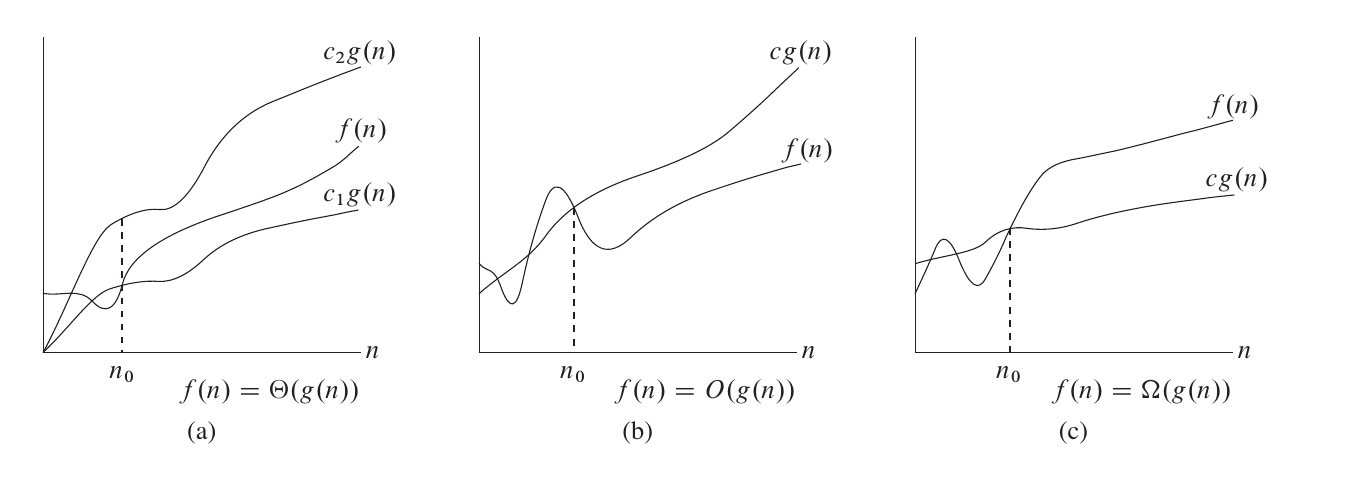
2.2.1 Ký hiệu tiệm cận chặt chẽ $\Theta$

Ký hiệu tiệm cận chặt chẽ $\Theta$ : Đối với hai hàm $f(n)$ và $g(n)$ , $f(n) = \Theta(g(n))$ . Tồn tại các hằng số dương $c_1$ , $c_2$ và $n_0$ sao cho đối với tất cả các $n \ge n_0$ ，có $0 \le c_1 \cdot g(n) \le f(n) \le c_2 \cdot g(n)$ 。

Nghĩa là, nếu hàm $f(n) = \Theta(g(n))$ ，chúng ta có thể tìm thấy hai số dương $c_1$ , $c_2$ sao cho $f(n)$ nằm giữa $c_1 \cdot g(n)$ và $c_2 \cdot g(n)$ .

Ví dụ: $T(n) = 3n^2 + 4n + 5 = \Theta(n^2)$ ，chúng ta có thể tìm thấy $c_1 = 1$ , $c_2 = 12$ , $n_0 = 1$ sao cho với tất cả $n \ge 1$ ，đều có $n^2 \le 3n^2 + 4n + 5 \le 12n^2$ 。

2.2.2 Ký hiệu tiệm cận trên $O$

Ký hiệu tiệm cận trên $O$ : Đối với hai hàm $f(n)$ và $g(n)$ , $f(n) = O(g(n))$ 。Tồn tại một hằng số dương $c$ và $n_0$ sao cho khi $n > n_0$ ，có $0 \le f(n) \le c \cdot g(n)$ 。

Ký hiệu $O$ chỉ cho ta biết một hàm là một giới hạn trên của hàm khác.

2.2.3 Ký hiệu tiệm cận dưới $\Omega$

Ký hiệu tiệm cận dưới $\Omega$ : Đối với hai hàm $f(n)$ và $g(n)$ , $f(n) = \Omega(g(n))$ 。Tồn tại một hằng số dương $c$ và $n_0$ sao cho khi $n > n_0$ ，có $0 \le c \cdot g(n) \le f(n)$ 。

Tương tự, nếu chúng ta chỉ biết giới hạn dưới của một hàm, chúng ta có thể sử dụng ký hiệu $\Omega$ .

2.3 Tính toán độ phức tạp thời gian

Các ký hiệu tiệm cận có thể được sử dụng để mô tả giới hạn trên và giới hạn dưới của một hàm, đồng thời cũng có thể được sử dụng để mô tả xu hướng tăng của thời gian thực hiện của thuật toán.

Khi tính toán độ phức tạp thời gian, chúng ta thường sử dụng ký hiệu tiệm cận trên $O$ . Bởi vì chúng ta thường quan tâm đến giới hạn trên của thời gian thực hiện thuật toán, không quan tâm đến giới hạn dưới của nó.

Vậy làm thế nào để tính toán độ phức tạp thời gian?

Quá trình tính toán độ phức tạp thời gian thường bao gồm các bước sau:

Xác định các thao tác cơ bản trong thuật toán: Các thao tác cơ bản là các câu lệnh trong thuật toán được thực hiện nhiều nhất, thường là phần thân của vòng lặp ở cấp độ lồng nhau sâu nhất.
Tính toán thứ tự của số lần thực hiện các thao tác cơ bản: Chỉ cần tính toán thứ tự của số lần thực hiện các thao tác cơ bản, đảm bảo rằng bậc cao nhất của hàm là chính xác. Các hệ số của bậc cao nhất và các bậc thấp hơn có thể bị bỏ qua.
Sử dụng ký hiệu Big O để biểu thị độ phức tạp thời gian: Đặt thứ tự tính toán từ bước trước vào ký hiệu O tiệm cận trên.

Đồng thời, khi tính toán độ phức tạp thời gian, cũng cần lưu ý một số nguyên tắc:

Nguyên tắc cộng: Độ phức tạp thời gian tổng cộng bằng độ phức tạp thời gian của thao tác cơ bản có thứ tự lớn nhất.

Nếu $T_1(n) = O(f_1(n))$ ， $T_2(n) = O(f_2(n))$ ， $T(n) = T_1(n) + T_2(n)$ ，thì $T(n) = O(f(n)) = \max(O(f_1(n)), O(f_2(n))) = O(\max(f_1(n), f_2(n)))$ .

Nguyên tắc nhân: Độ phức tạp thời gian của đoạn mã lặp lồng nhau bằng tích của độ phức tạp thời gian của các thao tác cơ bản lồng nhau.

Nếu $T_1 = O(f_1(n))$ ， $T_2 = O(f_2(n))$ ， $T(n) = T_1(n) \cdot T_2(n)$ ，thì $T(n) = O(f(n)) = O(f_1(n)) \cdot O(f_2(n)) = O(f_1(n) \cdot f_2(n))$ .

Dưới đây là một ví dụ cụ thể để giải thích cách tính toán độ phức tạp thời gian.

2.3.1 Hằng số $O(1)$

Trong hầu hết các trường hợp, nếu thuật toán không có vòng lặp, không có đệ quy, thì độ phức tạp thời gian của nó là $O(1)$ .

$O(1)$ chỉ là một cách biểu thị cho độ phức tạp thời gian của hằng số, không phải chỉ có một dòng mã được thực thi. Miễn là thời gian thực hiện mã không tăng lên theo kích thước của vấn đề $n$ tăng lên, thuật toán đó sẽ có độ phức tạp thời gian là $O(1)$ .

def algorithm(n):
    a = 1
    b = 2
    res = a * b + n
    return res

Mã trên mặc dù có $4$ dòng mã, nhưng độ phức tạp thời gian của nó vẫn là $O(1)$ , không phải là $O(3)$ .

2.3.2 Tuyến tính $O(n)$

Trong hầu hết các trường hợp, nếu có vòng lặp không lồng nhau và số lần thực hiện các câu lệnh trong vòng lặp là $n$ thì thuật toán có độ phức tạp thời gian tuyến tính. Loại thuật toán này có thời gian thực hiện tăng tuyến tính theo kích thước của vấn đề $n$ .

def algorithm(n):
    sum = 0
    for i in range(n):
        sum += 1
    return sum

Trong đoạn mã trên, số lần thực hiện câu lệnh sum += 1 là $n$ lần, vì vậy độ phức tạp thời gian của đoạn mã này là $O(n)$ .

2.3.3 Bậc hai $O(n^2)$

Các thuật toán có hai lớp lồng nhau và số lần thực hiện câu lệnh trong mỗi lớp vòng lặp là $n$ có thời gian chạy bậc hai. Loại thuật toán này tăng theo bậc hai khi kích thước của vấn đề $n$ tăng lên.

def algorithm(n):
    res = 0
    for i in range(n):
        for j in range(n):
            res += 1
    return res

Trong đoạn mã trên, câu lệnh res += 1 được thực hiện trong hai vòng lặp lồng nhau, theo nguyên tắc nhân của độ phức tạp thời gian, số lần thực hiện đoạn mã này là $n^2$ lần, vì vậy độ phức tạp thời gian của nó là $O(n^2)$ .

2.3.4 Giai thừa $O(n!)$

Độ phức tạp thời gian giai thừa thường xuất hiện trong các thuật toán liên quan đến "sắp xếp hoàn toàn" hoặc "giải quyết bài toán người du lịch theo cách tìm kiếm vét cạn". Loại thuật toán này tăng theo giai thừa khi kích thước của vấn đề $n$ tăng lên.

def permutations(arr, start, end):
    if start == end:
        print(arr)
        return

    for i in range(start, end):
        arr[i], arr[start] = arr[start], arr[i]
        permutations(arr, start + 1, end)
        arr[i], arr[start] = arr[start], arr[i]

Trong đoạn mã trên, thuật toán "sắp xếp đầy đủ" được thực hiện bằng phương pháp đệ quy. Giả sử độ dài của mảng $arr$ là $n$ , vòng lặp for ở tầng thứ nhất thực hiện $n$ lần, vòng lặp for ở tầng thứ hai thực hiện $n - 1$ lần. Tiếp tục như vậy, vòng lặp for ở tầng cuối cùng thực hiện 1 lần. Tổng số lần thực hiện của tất cả các vòng lặp là $n \times (n - 1) \times (n - 2) \times … \times 2 \times 1 = n!$ lần. Do đó, số lần thực hiện của câu lệnh cơ bản trong vòng lặp for là $n!$ lần, vì vậy độ phức tạp thời gian tương ứng là $O(n!)$ .

2.3.5 Logarithm $O(\log n)$

Thời gian chạy theo độ phức tạp logarithm thường xuất hiện trong các thuật toán "tìm kiếm nhị phân" hoặc "chia để trị" khi chia một vấn đề thành hai phần. Loại thuật toán này tăng theo độ phức tạp logarithm khi kích thước của vấn đề $n$ tăng lên.

def algorithm(n):
    cnt = 1
    while cnt < n:
        cnt *= 2
    return cnt

Trong đoạn mã trên, thời gian chạy của cnt = 1 là $O(1)$ và có thể bỏ qua. Trong vòng lặp while, biến cnt bắt đầu từ $1$ và nhân với $2$ sau mỗi vòng lặp. Khi cnt lớn hơn hoặc bằng $n$ , vòng lặp kết thúc. Giá trị của biến cnt tạo thành một dãy số học: $2^0, 2^1, 2^2, …, 2^x$ , dựa trên phương trình $2^x = n$ , ta có thể suy ra số lần thực hiện vòng lặp này là $\log_2n$ lần, do đó độ phức tạp thời gian của đoạn mã này là $O(\log_2n)$ .

Vì $\log n = k \times \log_2 n$ , với $k = 3.322$ , nên sự khác biệt giữa $\log n$ và $\log_2 n$ khá nhỏ. Để tiện viết, thường ta viết độ phức tạp thời gian theo dạng $O(\log n)$ .

2.3.6 Linearithmic $O(n \times \log n)$

Độ phức tạp thời gian linearithmic thường xuất hiện trong các thuật toán sắp xếp như "quick sort", "merge sort", "heap sort", v.v. Loại thuật toán này tăng theo độ phức tạp linearithmic khi kích thước của vấn đề $n$ tăng lên.

def algorithm(n):
    cnt = 1
    res = 0
    while cnt < n:
        cnt *= 2
        for i in range(n):
            res += 1
    return res

Trong đoạn mã trên, độ phức tạp thời gian của vòng lặp bên ngoài là $O(\log n)$ , độ phức tạp thời gian của vòng lặp bên trong là $O(n)$ , và hai vòng lặp này độc lập với nhau. Do đó, độ phức tạp thời gian tổng thể là $O(n \times \log n)$ .

2.3.7 Các mối quan hệ Độ phức tạp thời gian thường gặp

Sắp xếp theo thứ tự tăng dần, các Độ phức tạp thời gian thường gặp là: $O(1)$ < $O(\log n)$ < $O(n)$ < $O(n \times \log n)$ < $O(n^2)$ < $O(n^3)$ < $O(2^n)$ < $O(n!)$ < $O(n^n)$ .

2.4 Độ phức tạp thời gian tốt nhất, tệ nhất và trung bình

Độ phức tạp thời gian là một hàm phụ thuộc vào kích thước của vấn đề đầu vào $n$ . Tuy nhiên, do nội dung của vấn đề đầu vào có thể khác nhau, chúng ta thường chia "Độ phức tạp thời gian" thành ba trường hợp: "tốt nhất", "xấu nhất" và "trung bình". Ý nghĩa cụ thể của ba trường hợp này như sau:

Độ phức tạp thời gian tốt nhất: Độ phức tạp thời gian của đầu vào mà có thời gian thực thi ngắn nhất trong tất cả các kích thước đầu vào.
Độ phức tạp thời gian xấu nhất: Độ phức tạp thời gian của đầu vào mà có thời gian thực thi dài nhất trong tất cả các kích thước đầu vào.
Độ phức tạp thời gian trung bình: Độ phức tạp thời gian trung bình của tất cả các đầu vào có thể có (Độ phức tạp thời gian trung bình theo kỳ vọng trong trường hợp đầu vào ngẫu nhiên).

Chúng ta sẽ phân tích ví dụ sau để hiểu rõ hơn về Độ phức tạp thời gian tốt nhất, xấu nhất và trung bình.

def find(nums, val):
    pos = -1
    for i in range(n):
        if nums[i] == val:
            pos = i
            break
    return pos

Đoạn mã trên được sử dụng để tìm vị trí của biến có giá trị $val$ trong một mảng số nguyên $nums$ . Nếu không xét đến câu lệnh break, theo phân tích trong phần "2.3 Độ phức tạp thời gian", thì Độ phức tạp thời gian của thuật toán này là $O(n)$ , trong đó $n$ là độ dài của mảng.

Tuy nhiên, nếu xét đến câu lệnh break, chúng ta cần xem xét nội dung đầu vào. Nếu giá trị của phần tử đầu tiên trong mảng $nums$ chính là $val$ , thì không cần duyệt qua các phần tử còn lại, Độ phức tạp thời gian sẽ là $O(1)$ , tức là Độ phức tạp thời gian tốt nhất là $O(1)$ . Nếu mảng không chứa biến có giá trị $val$ , thì cần duyệt qua toàn bộ mảng, Độ phức tạp thời gian sẽ là $O(n)$ , tức là Độ phức tạp thời gian xấu nhất là $O(n)$ .

Như vậy, Độ phức tạp thời gian không còn là duy nhất. Làm thế nào để giải quyết?

Chúng ta đều biết rằng, độ phức tạp thời gian tốt nhất và độ phức tạp thời gian xấu nhất chỉ xảy ra trong các trường hợp cực đoan, và xác suất xảy ra thực sự rất nhỏ. Để có thể mô tả tốt hơn độ phức tạp thời gian trong điều kiện bình thường, chúng ta thường sử dụng độ phức tạp thời gian trung bình làm cách tính độ phức tạp thời gian.

Trong ví dụ trên, để tìm vị trí của biến có giá trị $val$ trong mảng $nums$ , có tổng cộng $n + 1$ trường hợp: "có trong mảng từ vị trí $0$ đến $n - 1$ " và "không có trong mảng". Chúng ta tính tổng số lần thực hiện câu lệnh trong tất cả các trường hợp, sau đó chia cho $n + 1$ , sẽ thu được số lần thực hiện trung bình, tức là $\frac{1 + 2 + 3 + … + n + n}{n + 1} = \frac{n(n + 3)}{2(n + 1)}$ . Sau khi rút gọn biểu thức, ta thu được độ phức tạp thời gian trung bình là $O(n)$ .

Thường thì chỉ khi cùng một thuật toán có sự khác biệt về độ phức tạp thời gian đáng kể giữa các trường hợp đầu vào khác nhau, chúng ta mới sử dụng ba cách tính độ phức tạp thời gian này để phân biệt. Trong hầu hết các trường hợp, chỉ cần sử dụng một trong ba cách tính độ phức tạp thời gian là đủ.

3. Độ phức tạp không gian

3.1 Giới thiệu về độ phức tạp không gian

Độ phức tạp không gian (Space Complexity): Là kích thước không gian mà thuật toán sử dụng dựa trên kích thước đầu vào $n$ của vấn đề. Độ phức tạp không gian thường được ký hiệu là $S(n)$ . Thông thường, không gian phụ trợ của thuật toán được sử dụng để đo lường độ phức tạp không gian.

Ngoài thời gian thực thi, số lượng không gian lưu trữ mà thuật toán sử dụng cũng là một yếu tố quan trọng để đánh giá hiệu suất. Các biểu thức đánh giá độ phức tạp không gian cũng áp dụng các biểu tượng tăng trưởng tương tự như độ phức tạp thời gian. Độ phức tạp không gian có thể được biểu diễn dưới dạng $S(n) = O(f(n))$ , trong đó độ phức tạp không gian tăng theo cùng một xu hướng với hàm $f(n)$ khi kích thước vấn đề $n$ tăng lên.

So với việc tính toán độ phức tạp thời gian của thuật toán, tính toán độ phức tạp không gian dễ hơn và chủ yếu bao gồm hai phần: "không gian lưu trữ mà biến cục bộ (biến được định nghĩa trong phạm vi thuật toán) chiếm" và "không gian ngăn xếp mà hệ thống sử dụng để thực hiện đệ quy (nếu thuật toán là đệ quy)".

Dưới đây là một ví dụ để minh họa cách tính toán độ phức tạp không gian.

3.1 Tính toán độ phức tạp không gian

3.1.1 Hằng số $O(1)$

def algorithm(n):
    a = 1
    b = 2
    res = a * b + n
    return res

Trong đoạn mã trên, chúng ta sử dụng $a$ , $b$ , và $res$ là ba biến cục bộ. Kích thước không gian mà chúng chiếm giữ là hằng số và không tăng theo kích thước vấn đề $n$ . Do đó, độ phức tạp không gian của thuật toán này là $O(1)$ .

3.1.2 Tuyến tính $O(n)$

def algorithm(n):
    if n <= 0:
        return 1
    return n * algorithm(n - 1)

Trong đoạn mã trên, chúng ta sử dụng đệ quy. Mỗi lần gọi đệ quy chiếm một khung ngăn xếp, và tổng cộng có $n$ lần gọi đệ quy. Do đó, độ phức tạp không gian của thuật toán này là $O(n)$ .

3.1.3 Mối quan hệ độ phức tạp không gian thông thường

Sắp xếp theo thứ tự tăng dần, các độ phức tạp không gian thông thường là: $O(1)$ < $O(\log n)$ < $O(n)$ < $O(n^2)$ < $O(2^n)$ và các giá trị tương tự.

Tổng kết về độ phức tạp của thuật toán

"Độ phức tạp của thuật toán" bao gồm "độ phức tạp thời gian" và "độ phức tạp không gian", được sử dụng để phân tích mối quan hệ giữa hiệu suất thực thi của thuật toán và kích thước đầu vào $n$ . Thông thường, chúng được biểu diễn bằng "biểu tượng tiệm cận".

Các độ phức tạp thời gian phổ biến bao gồm: $O(1)$ , $O(\log n)$ , $O(n)$ , $O(n \times \log n)$ , $O(n^2)$ , $O(n^3)$ , $O(2^n)$ , $O(n!)$ .

Các độ phức tạp không gian phổ biến bao gồm: $O(1)$ å, $O(\log n)$ , $O(n)$ , $O(n^2)$ .
π