Segment Tree
1. Giới thiệu cây phân đoạn
1.1 Định nghĩa cây phân đoạn
Cây phân đoạn (Segment Tree, Interval Tree): Là một loại cây nhị phân dựa trên ý tưởng chia để trị, được sử dụng để thống kê thông tin trên một đoạn. Mỗi nút trong cây đều tương ứng với một đoạn
[left, right], trong đóleftvàrightthường là các số nguyên. Mỗi nút lá đại diện cho một đoạn đơn vị (có độ dài bằng1), nút lá tương ứng với đoạn cóleft == right. Mỗi nút không phải lá[left, right], nút con trái của nó đại diện cho đoạn[left, (left + right) / 2], nút con phải đại diện cho đoạn[(left + right) / 2 + 1, right].
Cây phân đoạn là một cây nhị phân cân bằng, mỗi nút trên cây đều duy trì một đoạn. Nút gốc duy trì toàn bộ đoạn, mỗi nút duy trì một phần đoạn được chia đều từ đoạn của nút cha. Khi có n phần tử, các phép toán trên đoạn (cập nhật điểm đơn, cập nhật đoạn, truy vấn đoạn, v.v.) có thể được thực hiện trong thời gian phức tạp .
Dưới đây là một ví dụ về cây phân đoạn với đoạn [0, 7].
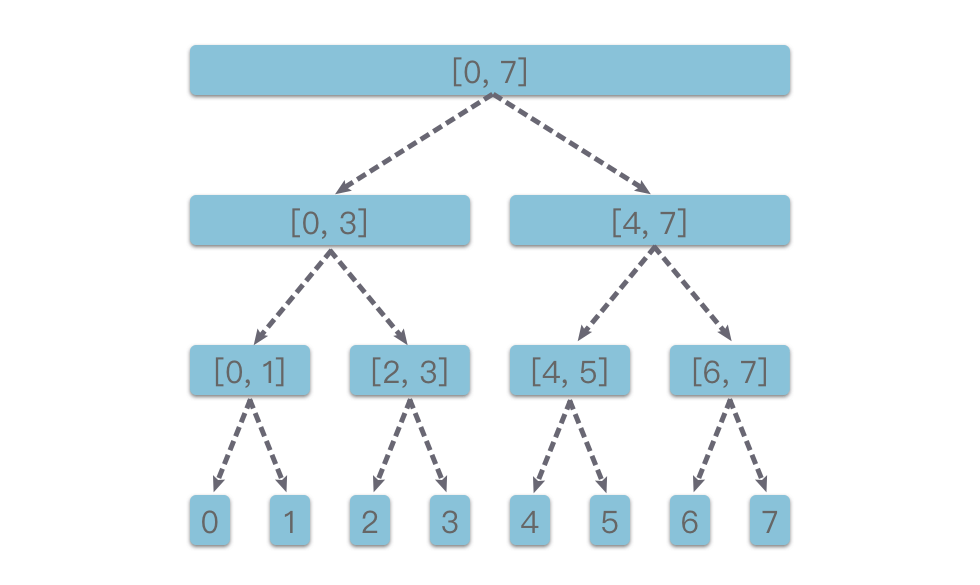
1.2 Đặc điểm của cây phân đoạn
Dựa trên mô tả trên, chúng ta có thể tóm tắt các đặc điểm của cây phân đoạn:
- Mỗi nút trong cây phân đoạn đại diện cho một đoạn.
- cây phân đoạn có một nút gốc duy nhất, đại diện cho toàn bộ đoạn thống kê, ví dụ
[1, n]. - Mỗi nút lá trong cây đại diện cho một đoạn đơn vị có độ dài
1, ví dụ[x, x]. - Đối với mỗi nút trong cây không phải lá
[left, right], nút con trái của nó đại diện cho đoạn[left, mid], nút con phải đại diện cho đoạn[mid + 1, right]. Trong đó,mid = (left + right) / 2(làm tròn xuống).
2. Xây dựng cây phân đoạn
2.1 Cấu trúc lưu trữ của cây phân đoạn
Trước đó, chúng ta đã học về hai cấu trúc lưu trữ của cây nhị phân, một là "cấu trúc lưu trữ dạng liên kết" và hai là "cấu trúc lưu trữ dạng tuần tự". cây phân đoạn cũng có thể được triển khai bằng cả hai cấu trúc lưu trữ này.
Vì cây phân đoạn gần như là một cây nhị phân đầy đủ, nên rất phù hợp để sử dụng "cấu trúc lưu trữ dạng tuần tự" để triển khai.
Chúng ta có thể sử dụng phương pháp đánh số tương tự với cây nhị phân đầy đủ để đánh số cây phân đoạn. Cách thức như sau:
- Nút gốc có số thứ tự là
0. - Nếu nút nhị phân (không phải nút lá) có chỉ số là
i, thì nút con trái của nó có chỉ số2 * i + 1, nút con phải có chỉ số2 * i + 2. - Nếu nút nhị phân (không phải nút gốc) có chỉ số là
i, thì nút cha của nó có chỉ số(i - 1) // 2,//là phép chia lấy phần nguyên.
Như vậy, chúng ta có thể sử dụng một mảng để lưu trữ cây phân đoạn. Kích thước của mảng này nên được đặt là bao nhiêu?
- Trong trường hợp lý tưởng, cây phân đoạn được tạo thành từ
nđơn vị đoạn sẽ là một cây nhị phân đầy đủ, số lượng nút là . Vì , nên trong trường hợp lý tưởng, chỉ cần sử dụng một mảng có kích thước là để lưu trữ cây phân đoạn là đủ. - Tuy nhiên, trong trường hợp chung, một số đoạn cần phải mở rộng thêm một lớp để lưu trữ các phần tử. Độ sâu của cây phân đoạn là , trong trường hợp xấu nhất, số lượng nút lá (bao gồm cả các nút không cần thiết) là , tổng số nút là , có thể xem như là , vì vậy chúng ta có thể sử dụng một mảng có kích thước là để lưu trữ cây phân đoạn.
2.2 Phương pháp xây dựng cây phân đoạn
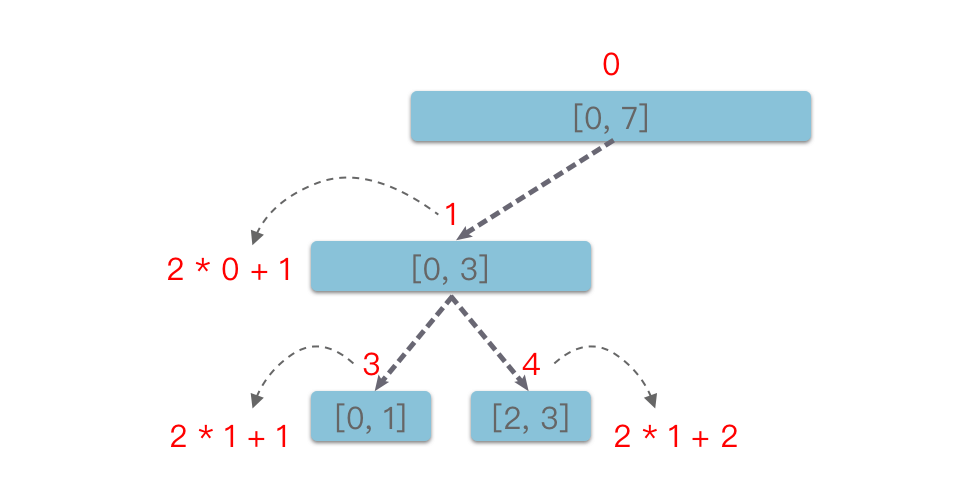
Dựa vào hình trên, ta có thể thấy: Nút con trái của nút có chỉ số i là 2 * i + 1, nút con phải là 2 * i + 2. Do đó, cây phân đoạn rất phù hợp để sử dụng phương pháp đệ quy để tạo ra. Các bước cụ thể như sau:
- Nếu đó là nút lá (
left == right), giá trị của nút là giá trị của phần tử tại vị trí tương ứng. - Nếu đó là nút không phải lá, tiếp tục đệ quy tạo cây con trái và cây con phải.
- Giá trị của nút là kết quả của phép gộp giữa giá trị của nút con trái và nút con phải.
Đoạn mã dưới đây triển khai việc xây dựng cây phân đoạn:
# Lớp nút của cây phân đoạn
class TreeNode:
def __init__(self, val=0):
self.left = -1 # Giới hạn trái của đoạn
self.right = -1 # Giới hạn phải của đoạn
self.val = val # Giá trị của nút (giá trị của đoạn)
self.lazy_tag = None # Nhãn trì hoãn cập nhật cho vấn đề tổng đoạn
# Lớp cây phân đoạn
class SegmentTree:
def __init__(self, nums, function):
self.size = len(nums)
self.tree = [TreeNode() for _ in range(4 * self.size)] # Mảng TreeNode để lưu trữ
self.nums = nums # Dữ liệu gốc
self.function = function # function là một hàm, phương pháp gộp hai đoạn trái và phải
if self.size > 0:
self.__build(0, 0, self.size - 1)
# Xây dựng cây phân đoạn, chỉ số lưu trữ của nút là index, đoạn của nút là [left, right]
def __build(self, index, left, right):
self.tree[index].left = left
self.tree[index].right = right
if left == right: # Nút lá, giá trị của nút là giá trị của phần tử tại vị trí tương ứng
self.tree[index].val = self.nums[left]
return
mid = left + (right - left) // 2 # Điểm chia đoạn trái và phải
left_index = index * 2 + 1 # Chỉ số lưu trữ của nút con trái
right_index = index * 2 + 2 # Chỉ số lưu trữ của nút con phải
self.__build(left_index, left, mid) # Đệ quy tạo cây con trái
self.__build(right_index, mid + 1, right) # Đệ quy tạo cây con phải
self.__pushup(index) # Cập nhật giá trị đoạn của nút lên trên
# Cập nhật giá trị đoạn của nút có chỉ số index lên trên, giá trị đoạn của nút là kết quả gộp giữa giá trị của nút con trái và nút con phải
def __pushup(self, index):
left_index = index * 2 + 1 # Chỉ số lưu trữ của nút con trái
right_index = index * 2 + 2 # Chỉ số lưu trữ của nút con phải
self.tree[index].val = self.function(self.tree[left_index].val, self.tree[right_index].val)Ở đây, function đề cập đến phương pháp gộp đoạn của cây phân đoạn. Nó có thể được thay đổi dựa trên yêu cầu của bài toán, các phép toán phổ biến bao gồm tổng, tìm giá trị lớn nhất, tìm giá trị nhỏ nhất, v.v.
3. Các thao tác cơ bản trên cây phân đoạn
Các thao tác cơ bản trên cây phân đoạn bao gồm cập nhật điểm đơn, truy vấn đoạn và cập nhật đoạn. Dưới đây chúng ta sẽ đi vào từng thao tác một.
3.1 Cập nhật điểm đơn trên cây phân đoạn
Cập nhật điểm đơn trên cây phân đoạn: Thay đổi giá trị của một phần tử, ví dụ như thay đổi
nums[i]thànhval.
Chúng ta có thể sử dụng phương pháp đệ quy để cập nhật điểm đơn, các bước cụ thể như sau:
- Nếu đó là nút lá, tức là
left == right, thì cập nhật giá trị của nút đó. - Nếu đó là nút không phải lá, thì xác định xem nên cập nhật trong cây con trái hay cây con phải.
- Cập nhật giá trị của nút trong cây con trái hoặc cây con phải tương ứng.
- Sau khi cập nhật cây con trái và cây con phải, cập nhật giá trị đoạn của nút lên trên (tổng đoạn, giá trị lớn nhất của đoạn, giá trị nhỏ nhất của đoạn, v.v.).
Dưới đây là mã code thực hiện cập nhật điểm đơn trên cây phân đoạn:
# Cập nhật điểm đơn, thay đổi nums[i] thành val
def update_point(self, i, val):
self.nums[i] = val
self.__update_point(i, val, 0, 0, self.size - 1)
# Cập nhật điểm đơn, thay đổi nums[i] thành val. Chỉ số lưu trữ của nút là index, đoạn của nút là [left, right]
def __update_point(self, i, val, index, left, right):
if self.tree[index].left == self.tree[index].right:
self.tree[index].val = val # Nút lá, cập nhật giá trị của nút thành val
return
mid = left + (right - left) // 2 # Điểm chia đoạn trái và phải
left_index = index * 2 + 1 # Chỉ số lưu trữ của nút con trái
right_index = index * 2 + 2 # Chỉ số lưu trữ của nút con phải
if i <= mid: # Cập nhật trong cây con trái
self.__update_point(i, val, left_index, left, mid)
else: # Cập nhật trong cây con phải
self.__update_point(i, val, right_index, mid + 1, right)
self.__pushup(index) # Cập nhật giá trị đoạn của nút lên trên3.2 Truy vấn đoạn trên cây phân đoạn
Truy vấn đoạn trên cây phân đoạn: Truy vấn giá trị của một đoạn
[q_left, q_right].
Chúng ta có thể sử dụng phương pháp đệ quy để thực hiện truy vấn đoạn, các bước cụ thể như sau:
- Nếu đoạn
[q_left, q_right]hoàn toàn bao phủ đoạn[left, right]của nút hiện tại, tức làleft >= q_leftvàright <= q_right, thì trả về giá trị đoạn của nút đó. - Nếu đoạn
[q_left, q_right]và đoạn[left, right]không liên quan gì nhau, tức làright < q_lefthoặcleft > q_right, thì trả về0. - Nếu đoạn
[q_left, q_right]và đoạn[left, right]có giao nhau, thực hiện các bước sau:- Nếu đoạn
[q_left, q_right]có giao với đoạn con trái[left, mid]của nút hiện tại, tức làq_left <= mid, thì thực hiện truy vấn trong cây con trái và lưu kết quả truy vấnres_left. - Nếu đoạn
[q_left, q_right]có giao với đoạn con phải[mid + 1, right]của nút hiện tại, tức làq_right > mid, thì thực hiện truy vấn trong cây con phải và lưu kết quả truy vấnres_right. - Cuối cùng, trả về kết quả của phép gộp giữa kết quả truy vấn cây con trái và cây con phải.
- Nếu đoạn
Dưới đây là mã code thực hiện truy vấn đoạn trên cây phân đoạn:
# Truy vấn đoạn, truy vấn giá trị của đoạn [q_left, q_right]
def query_interval(self, q_left, q_right):
return self.__query_interval(q_left, q_right, 0, 0, self.size - 1)
# Truy vấn đoạn, tìm kiếm giá trị của đoạn [q_left, q_right] trong đoạn [left, right] của cây phân đoạn
def __query_interval(self, q_left, q_right, index, left, right):
if left >= q_left and right <= q_right: # Đoạn của nút được bao phủ bởi [q_left, q_right]
return self.tree[index].val # Trả về giá trị của nút
if right < q_left or left > q_right: # Đoạn của nút không liên quan đến [q_left, q_right]
return 0
self.__pushdown(index)
mid = left + (right - left) // 2 # Điểm chia đoạn trái và phải
left_index = index * 2 + 1 # Chỉ số lưu trữ của nút con trái
right_index = index * 2 + 2 # Chỉ số lưu trữ của nút con phải
res_left = 0 # Kết quả truy vấn cây con trái
res_right = 0 # Kết quả truy vấn cây con phải
if q_left <= mid: # Truy vấn trong cây con trái
res_left = self.__query_interval(q_left, q_right, left_index, left, mid)
if q_right > mid: # Truy vấn trong cây con phải
res_right = self.__query_interval(q_left, q_right, right_index, mid + 1, right)
return self.function(res_left, res_right) # Trả về kết quả của phép gộp giữa kết quả truy vấn cây con trái và cây con phải3.3 Cập nhật đoạn trên cây phân đoạn
Cập nhật đoạn trên cây phân đoạn: Cập nhật giá trị của đoạn
[q_left, q_right]thànhval.
3.3.1 Nhãn trì hoãn
Khi thực hiện các thao tác cập nhật điểm đơn và truy vấn đoạn trên cây phân đoạn, đoạn [q_left, q_right] trên cây phân đoạn sẽ được chia thành đoạn nhỏ (nút), từ đó thực hiện các thao tác trong thời gian phức tạp .
Tuy nhiên, trong trường hợp của "cập nhật đoạn", nếu đoạn [q_left, q_right] hoàn toàn bao phủ đoạn [left, right] của nút hiện tại, tức là left >= q_left và right <= q_right thì tất cả các nút trong cây con của nút hiện tại đều phải thay đổi giá trị. Nếu thực hiện cập nhật từng nút một, thì thời gian thực hiện cập nhật đoạn sẽ tăng lên .
Với ý tưởng giảm số lần cập nhật và thời gian thực hiện, chúng ta có thể thêm một "nhãn trì hoãn" vào lớp nút của cây phân đoạn, đánh dấu rằng "đoạn này đã được cập nhật thành val, nhưng giá trị của các nút con chưa được cập nhật". Điều này có nghĩa là thay vì cập nhật từng nút con khi thực hiện cập nhật đoạn, chúng ta sẽ trì hoãn việc cập nhật cho các nút con cho đến khi chúng được truy cập trong các thao tác sau (khi đệ quy vào các nút con). Điều này giúp giảm thời gian thực hiện cập nhật đoạn và truy vấn đoạn xuống .
Các bước thực hiện cập nhật đoạn với nhãn trì hoãn như sau:
- Nếu đoạn
[q_left, q_right]hoàn toàn bao phủ đoạn[left, right]của nút hiện tại, tức làleft >= q_leftvàright <= q_right, thì cập nhật giá trị của đoạn nút hiện tại và đánh dấu nhãn trì hoãn của nút hiện tại là giá trị đoạn. - Nếu đoạn
[q_left, q_right]và đoạn[left, right]không liên quan gì nhau, tức làright < q_lefthoặcleft > q_right, thì trả về. - Nếu đoạn
[q_left, q_right]và đoạn[left, right]có giao nhau, thực hiện các bước sau:- Nếu nút hiện tại đã được đánh dấu nhãn trì hoãn, tức là nhãn trì hoãn không phải là
None, thì áp dụng thao tác cập nhật đoạn cho các nút con của nút hiện tại (tức là cập nhật xuống). - Nếu đoạn
[q_left, q_right]có giao với đoạn con trái[left, mid]của nút hiện tại, tức làq_left <= mid, thì thực hiện cập nhật đoạn trong cây con trái. - Nếu đoạn
[q_left, q_right]có giao với đoạn con phải[mid + 1, right]của nút hiện tại, tức làq_right > mid, thì thực hiện cập nhật đoạn trong cây con phải. - Sau khi cập nhật cây con trái và cây con phải, cập nhật giá trị đoạn của nút hiện tại (tổng đoạn, giá trị lớn nhất của đoạn, giá trị nhỏ nhất của đoạn, v.v.).
- Nếu nút hiện tại đã được đánh dấu nhãn trì hoãn, tức là nhãn trì hoãn không phải là
3.3.2 Cập nhật xuống
Như đã đề cập ở trên, nếu nút hiện tại đã được đánh dấu nhãn trì hoãn, tức là nhãn trì hoãn không phải là None, thì chúng ta sẽ cập nhật giá trị đoạn cho các nút con của nút hiện tại (tức là cập nhật xuống). Các bước cụ thể của cập nhật xuống như sau:
- Cập nhật giá trị và nhãn trì hoãn của nút con trái thành
val. - Cập nhật giá trị và nhãn trì hoãn của nút con phải thành
val. - Cập nhật nhãn trì hoãn của nút hiện tại thành
None.
Dưới đây là mã code thực hiện cập nhật xuống với nhãn trì hoãn:
# Cập nhật xuống, cập nhật giá trị và nhãn trì hoãn của nút con trái và nút con phải của nút hiện tại
def __pushdown(self, index):
lazy_tag = self.tree[index].lazy_tag
if not lazy_tag:
return
left_index = index * 2 + 1 # Chỉ số lưu trữ của nút con trái
right_index = index * 2 + 2 # Chỉ số lưu trữ của nút con phải
self.tree[left_index].lazy_tag = lazy_tag # Cập nhật nhãn trì hoãn của nút con trái
left_size = (self.tree[left_index].right - self.tree[left_index].left + 1)
self.tree[left_index].val = lazy_tag * left_size # Cập nhật giá trị của nút con trái
self.tree[right_index].lazy_tag = lazy_tag # Cập nhật nhãn trì hoãn của nút con phải
right_size = (self.tree[right_index].right - self.tree[right_index].left + 1)
self.tree[right_index].val = lazy_tag * right_size # Cập nhật giá trị của nút con phải
self.tree[index].lazy_tag = None # Cập nhật nhãn trì hoãn của nút hiện tạiLưu ý: Trong một số bài toán, thay vì cập nhật đoạn
[q_left, q_right]thànhval, chúng ta có thể thay đổi giá trị của mỗi phần tử trong đoạn[q_left, q_right]bằng cách tăng hoặc giảmvaltừ giá trị hiện tại. Đối với trường hợp này, chúng ta có thể thay đổi định nghĩa của "nhãn trì hoãn".
Dưới đây là mã code thực hiện việc cập nhật tăng/giảm trong khoảng sử dụng "đánh dấu trì hoãn":
# Cập nhật khoảng, thay đổi giá trị các phần tử trong khoảng [q_left, q_right] thành val
def update_interval(self, q_left, q_right, val):
self.__update_interval(q_left, q_right, val, 0, 0, self.size - 1)
# Cập nhật khoảng
def __update_interval(self, q_left, q_right, val, index, left, right):
if left >= q_left and right <= q_right: # Khoảng của nút nằm trong khoảng [q_left, q_right]
# interval_size = (right - left + 1) # Kích thước khoảng của nút hiện tại
# self.tree[index].val = interval_size * val # Thay đổi giá trị của mỗi phần tử trong khoảng của nút hiện tại thành val
# self.tree[index].lazy_tag = val # Đánh dấu trì hoãn của nút hiện tại là giá trị của khoảng
if self.tree[index].lazy_tag:
self.tree[index].lazy_tag += val # Tăng giá trị đánh dấu trì hoãn của nút hiện tại thêm val
else:
self.tree[index].lazy_tag = val # Đặt giá trị đánh dấu trì hoãn của nút hiện tại là val
interval_size = (right - left + 1) # Kích thước khoảng của nút hiện tại
self.tree[index].val += val * interval_size # Tăng giá trị của mỗi phần tử trong khoảng của nút hiện tại thêm val
return
if right < q_left or left > q_right: # Khoảng của nút không liên quan đến khoảng [q_left, q_right]
return 0
self.__pushdown(index)
mid = left + (right - left) // 2 # Điểm chia khoảng thành hai nút con
left_index = index * 2 + 1 # Chỉ số lưu trữ của nút con bên trái
right_index = index * 2 + 2 # Chỉ số lưu trữ của nút con bên phải
if q_left <= mid: # Cập nhật giá trị khoảng trong cây con bên trái
self.__update_interval(q_left, q_right, val, left_index, left, mid)
if q_right > mid: # Cập nhật giá trị khoảng trong cây con bên phải
self.__update_interval(q_left, q_right, val, right_index, mid + 1, right)
self.__pushup(index)
# Cập nhật giá trị và đánh dấu trì hoãn của các nút con nằm trong khoảng của nút có chỉ số index
def __pushdown(self, index):
lazy_tag = self.tree[index].lazy_tag
if not lazy_tag:
return
left_index = index * 2 + 1 # Chỉ số lưu trữ của nút con bên trái
right_index = index * 2 + 2 # Chỉ số lưu trữ của nút con bên phải
if self.tree[left_index].lazy_tag:
self.tree[left_index].lazy_tag += lazy_tag # Cập nhật đánh dấu trì hoãn của nút con bên trái
else:
self.tree[left_index].lazy_tag = lazy_tag
left_size = (self.tree[left_index].right - self.tree[left_index].left + 1)
self.tree[left_index].val += lazy_tag * left_size # Tăng giá trị của mỗi phần tử trong khoảng của nút con bên trái thêm lazy_tag
if self.tree[right_index].lazy_tag:
self.tree[right_index].lazy_tag += lazy_tag # Cập nhật đánh dấu trì hoãn của nút con bên phải
else:
self.tree[right_index].lazy_tag = lazy_tag
right_size = (self.tree[right_index].right - self.tree[right_index].left + 1)
self.tree[right_index].val += lazy_tag * right_size # Tăng giá trị của mỗi phần tử trong khoảng của nút con bên phải thêm lazy_tag
self.tree[index].lazy_tag = None # Cập nhật đánh dấu trì hoãn của nút hiện tại4. Các loại bài toán thường gặp với cây phân đoạn
4.1 Bài toán RMQ
Bài toán RMQ: RMQ là viết tắt của Range Maximum / Minimum Query, nghĩa là cho một dãy số
numscó độ dàin, trả lời một số câu hỏiRMQ(nums, q_left, q_right), yêu cầu trả về giá trị lớn nhất (nhỏ nhất) của dãy sốnumstrong khoảng[q_left, q_right]. Đây là bài toán tìm giá trị lớn nhất (nhỏ nhất) trong một khoảng.
Giả sử số lần truy vấn là q, thì thời gian giải quyết bài toán RMQ bằng thuật toán thô sẽ là . Tuy nhiên, sử dụng cây phân đoạn để giải quyết bài toán RMQ sẽ có thời gian giải quyết từ đến .
4.2 Bài toán cập nhật điểm đơn, truy vấn khoảng
Bài toán cập nhật điểm đơn, truy vấn khoảng:
- Thay đổi giá trị của một phần tử.
- Truy vấn giá trị của khoảng
[q_left, q_right].
Loại bài toán này có thể giải quyết trực tiếp bằng "3.1 Cập nhật điểm đơn của cây phân đoạn" và "3.2 Truy vấn khoảng của cây phân đoạn".
4.3 Bài toán cập nhật khoảng, truy vấn khoảng
Bài toán cập nhật khoảng, truy vấn khoảng:
- Thay đổi giá trị của một khoảng.
- Truy vấn giá trị của khoảng
[q_left, q_right].
Loại bài toán này có thể giải quyết trực tiếp bằng "3.3 Cập nhật khoảng của cây phân đoạn" và "3.2 Truy vấn khoảng của cây phân đoạn".
4.4 Bài toán gộp khoảng
Bài toán gộp khoảng, truy vấn khoảng:
- Thay đổi giá trị của một khoảng.
- Truy vấn khoảng liên tiếp dài nhất trong khoảng
[q_left, q_right]thỏa mãn điều kiện nào đó.
Loại bài toán này yêu cầu thêm các biến thay đổi khi thực hiện cập nhật lên trên, cần gộp khoảng của các nút con khi thực hiện cập nhật lên trên.
4.5 Bài toán quét dọc
Bài toán quét dọc: Bài toán quét dọc hoặc quét mặt ảo để giải quyết các bài toán trong không gian Euclid, thường được sử dụng để giải quyết các bài toán về diện tích, chu vi, v.v.
Ý tưởng chính là: tưởng tượng một đường (thường là một đường dọc) di chuyển trên mặt phẳng, tại một số điểm dừng lại. Các phép toán hình học chỉ áp dụng cho các đối tượng hình học, và bất kỳ khi nào đường thẳng cắt hoặc tiếp xúc với các đối tượng, hoặc nằm cạnh đối tượng, chúng được coi là giao với đường quét hoặc kề sát đường quét, và khi đường thẳng cắt qua tất cả các đối tượng, có thể nhận được kết quả hoàn chỉnh.
Loại bài toán này thường có phạm vi tọa độ lớn, cần tiền xử lý tọa độ của mỗi đường quét bằng cách rời rạc hóa, ánh xạ tọa độ y thành 0, 1, 2, …. Sau đó, sử dụng cây phân đoạn để lưu trữ thông tin của mỗi đường dọc (tọa độ x, là đường dọc bên trái hay bên phải, v.v.), sau đó thực hiện gộp khoảng và thống kê thông tin liên quan.
5. Mở rộng của cây phân đoạn
5.1 cây phân đoạn mở rộng động
Trong một số trường hợp, cây phân đoạn cần duy trì một khoảng rất lớn (ví dụ: ), nhưng thực tế chỉ sử dụng một số lượng nhỏ các nút.
Nếu sử dụng cách triển khai mảng trước đây để xây dựng cây phân đoạn, thì cần sử dụng không gian kích thước , điều này tốn không gian quá lớn.
Lúc này, chúng ta có thể sử dụng ý tưởng mở rộng động để xây dựng cây phân đoạn.
Ý tưởng của cây phân đoạn mở rộng động như sau:
- Ban đầu, chỉ xây dựng một nút gốc, đại diện cho toàn bộ khoảng.
- Khi cần truy cập vào một cây con của cây phân đoạn (một phần khoảng con nào đó), sau đó xây dựng một nút đại diện cho khoảng con đó.
Mã nguồn triển khai cây phân đoạn mở rộng động như sau:
# Lớp nút của cây phân đoạn
class TreeNode:
def __init__(self, left=-1, right=-1, val=0):
self.left = left # Giới hạn trái của khoảng
self.right = right # Giới hạn phải của khoảng
self.mid = left + (right - left) // 2
self.leftNode = None # Nút con bên trái của khoảng
self.rightNode = None # Nút con bên phải của khoảng
self.val = val # Giá trị của nút (giá trị của khoảng)
self.lazy_tag = None # Nhãn trì hoãn cập nhật của vấn đề khoảng
# Lớp cây phân đoạn
class SegmentTree:
def __init__(self, function):
self.tree = TreeNode(0, int(1e9))
self.function = function # function là một hàm, phương pháp tổ hợp của khoảng bên trái và bên phải
# Cập nhật điểm, thay đổi nums[i] thành val
def update_point(self, i, val):
self.__update_point(i, val, self.tree)
# Cập nhật điểm, thay đổi nums[i] thành val. Khoảng của nút là [node.left, node.right]
def __update_point(self, i, val, node):
if node.left == node.right:
node.val = val # Nút lá, giá trị của nút được thay đổi thành val
return
if i <= node.mid: # Cập nhật giá trị trong cây con bên trái
if not node.leftNode:
node.leftNode = TreeNode(node.left, node.mid)
self.__update_point(i, val, node.leftNode)
else: # Cập nhật giá trị trong cây con bên phải
if not node.rightNode:
node.rightNode = TreeNode(node.mid + 1, node.right)
self.__update_point(i, val, node.rightNode)
self.__pushup(node) # Cập nhật giá trị khoảng của nút lên trên
# Truy vấn khoảng, truy vấn khoảng [q_left, q_right]
def query_interval(self, q_left, q_right):
return self.__query_interval(q_left, q_right, self.tree)
# Truy vấn khoảng, tìm kiếm trong khoảng [left, right] của cây phân đoạn để tìm khoảng [q_left, q_right]
def __query_interval(self, q_left, q_right, node):
if node.left >= q_left and node.right <= q_right: # Khoảng của nút nằm trong khoảng [q_left, q_right]
return node.val # Trả về giá trị của nút
if node.right < q_left or node.left > q_right: # Khoảng của nút không liên quan đến [q_left, q_right]
return 0
self.__pushdown(node) # Cập nhật giá trị và nhãn trì hoãn của nút và các nút con
res_left = 0 # Kết quả truy vấn của cây con bên trái
res_right = 0 # Kết quả truy vấn của cây con bên phải
if q_left <= node.mid: # Tìm kiếm trong cây con bên trái
if not node.leftNode:
node.leftNode = TreeNode(node.left, node.mid)
res_left = self.__query_interval(q_left, q_right, node.leftNode)
if q_right > node.mid: # Tìm kiếm trong cây con bên phải
if not node.rightNode:
node.rightNode = TreeNode(node.mid + 1, node.right)
res_right = self.__query_interval(q_left, q_right, node.rightNode)
return self.function(res_left, res_right) # Trả về kết quả tổ hợp của giá trị các nút con
# Cập nhật khoảng, thay đổi giá trị của khoảng [q_left, q_right] thành val
def update_interval(self, q_left, q_right, val):
self.__update_interval(q_left, q_right, val, self.tree)
# Cập nhật khoảng
def __update_interval(self, q_left, q_right, val, node):
if node.left >= q_left and node.right <= q_right: # Khoảng của nút nằm trong khoảng [q_left, q_right]
if node.lazy_tag:
node.lazy_tag += val # Tăng nhãn trì hoãn của nút hiện tại lên val
else:
node.lazy_tag = val # Gán nhãn trì hoãn của nút hiện tại thành val
interval_size = (node.right - node.left + 1) # Kích thước của khoảng hiện tại
node.val += val * interval_size # Tăng giá trị của từng phần tử trong khoảng hiện tại lên val
return
if node.right < q_left or node.left > q_right: # Khoảng của nút không liên quan đến [q_left, q_right]
return 0
self.__pushdown(node) # Cập nhật giá trị và nhãn trì hoãn của nút và các nút con
if q_left <= node.mid: # Cập nhật giá trị trong cây con bên trái
if not node.leftNode:
node.leftNode = TreeNode(node.left, node.mid)
self.__update_interval(q_left, q_right, val, node.leftNode)
if q_right > node.mid: # Cập nhật giá trị trong cây con bên phải
if not node.rightNode:
node.rightNode = TreeNode(node.mid + 1, node.right)
self.__update_interval(q_left, q_right, val, node.rightNode)
self.__pushup(node)
# Cập nhật giá trị và nhãn trì hoãn của nút và các nút con
def __pushdown(self, node):
lazy_tag = node.lazy_tag
if not node.lazy_tag:
return
if not node.leftNode:
node.leftNode = TreeNode(node.left, node.mid)
if not node.rightNode:
node.rightNode = TreeNode(node.mid + 1, node.right)
if node.leftNode.lazy_tag:
node.leftNode.lazy_tag += lazy_tag # Cập nhật nhãn trì hoãn của nút con bên trái
else:
node.leftNode.lazy_tag = lazy_tag # Gán nhãn trì hoãn của nút con bên trái thành lazy_tag
left_size = (node.leftNode.right - node.leftNode.left + 1)
node.leftNode.val += lazy_tag * left_size # Tăng giá trị của từng phần tử trong khoảng con bên trái lên lazy_tag
if node.rightNode.lazy_tag:
node.rightNode.lazy_tag += lazy_tag # Cập nhật nhãn trì hoãn của nút con bên phải
else:
node.rightNode.lazy_tag = lazy_tag # Gán nhãn trì hoãn của nút con bên phải thành lazy_tag
right_size = (node.rightNode.right - node.rightNode.left + 1)
node.rightNode.val += lazy_tag * right_size # Tăng giá trị của từng phần tử trong khoảng con bên phải lên lazy_tag
node.lazy_tag = None # Cập nhật nhãn trì hoãn của nút hiện tại thành None