Disjoint Set Union

1. Giới thiệu về Disjoint Set Union

1.1 Định nghĩa của Disjoint Set Union

Disjoint Set Union (hoặc Union-Find): Viết tắt là DSU, là một cấu trúc dữ liệu dạng cây được sử dụng để xử lý các vấn đề liên quan đến việc hợp nhất và truy vấn các tập hợp không giao nhau. Tập hợp không giao nhau đề cập đến một tập hợp các phần tử không trùng lặp.

Disjoint Set Union hỗ trợ hai phép toán chính:

• Hợp nhất (Union): Hợp nhất hai tập hợp thành một tập hợp.
• Tìm kiếm (Find): Xác định một phần tử thuộc tập hợp nào. Thông thường, nó trả về một phần tử "đại diện" trong tập hợp.

Disjoint Set Union thường được gọi là Union-Find vì chính 2 hoạt động chính của nó. Tôi thích dùng cái tên Union-Find hơn nên trong bài viết tôi sẽ sử dụng tên này!

Đơn giản mà nói, Disjoint Set Union được sử dụng để xử lý việc hợp nhất các tập hợp và truy vấn các tập hợp.

• "Tập hợp" trong Disjoint Set Union đề cập đến khái niệm tập hợp mà chúng ta đã học, trong đó không có các phần tử trùng lặp, tức là một tập hợp các phần tử không trùng lặp.
• "Hợp nhất" trong Disjoint Set Union đề cập đến phép toán hợp của các tập hợp, khi hai tập hợp được Hợp nhất lại thành một tập hợp. Phép toán Hợp nhất được thể hiện như sau:

{1, 3, 5, 7} ∪ {2, 4, 6, 8} = {1, 2, 3, 4, 5, 6, 7, 8}

• "Tìm kiếm" trong Disjoint Set Union áp dụng cho các phần tử được lưu trữ trong tập hợp. Thông thường, chúng ta cần tìm kiếm xem hai phần tử có thuộc cùng một tập hợp hay không.

Nếu chúng ta chỉ muốn biết một phần tử có thuộc tập hợp hay không, có thể sử dụng tập hợp set trong Python hoặc các ngôn ngữ khác. Tuy nhiên, nếu chúng ta muốn biết hai phần tử có thuộc cùng một tập hợp hay không, chỉ sử dụng một tập hợp set sẽ khó thực hiện được. Điều này đòi hỏi chúng ta sử dụng cấu trúc dữ liệu "Disjoint Set Union" mà chúng ta sẽ giới thiệu tiếp theo.

Dựa trên mô tả ở trên, chúng ta có thể định nghĩa các giao diện hoạt động của cấu trúc "Disjoint Set Union":

• Hợp nhất union(x, y): Hợp nhất tập hợp x và tập hợp y thành một tập hợp.
• Tìm kiếm find(x): Tìm kiếm phần tử x thuộc tập hợp nào.
• Truy vấn is_connected(x, y): Truy vấn xem phần tử x và y có thuộc cùng một tập hợp hay không.

1.2 Hai phương pháp triển khai của Union-Find

Dưới đây chúng ta sẽ trình bày hai phương pháp triển khai của Union-Find: một là sử dụng phương pháp "truy vấn nhanh" và triển khai dựa trên cấu trúc mảng; hai là sử dụng phương pháp "hợp nhất nhanh" và triển khai dựa trên cấu trúc cây.

1.2.1 Truy vấn nhanh: Triển khai dựa trên mảng

Nếu chúng ta muốn tăng hiệu suất truy vấn của Union-Find, chúng ta có thể tập trung vào các hoạt động truy vấn.

Khi triển khai Union-Find bằng phương pháp "truy vấn nhanh", chúng ta có thể sử dụng một "cấu trúc mảng" để biểu diễn các phần tử trong tập hợp. Mỗi phần tử trong mảng được gán một số hiệu là id. Sau đó, chúng ta có thể thực hiện các hoạt động sau trên mảng để triển khai Union-Find:

• Khi khởi tạo: Gán mỗi phần tử trong tập hợp một số hiệu tương ứng với chỉ số mảng. Điều này đảm bảo rằng id của mỗi phần tử là duy nhất, đại diện cho việc mỗi phần tử độc lập thuộc một tập hợp.
• Khi thực hiện hoạt động hợp nhất: Chúng ta cần thay đổi id của tất cả các phần tử trong một tập hợp thành id của tập hợp khác, điều này đảm bảo rằng tất cả các phần tử trong tập hợp sau khi hợp nhất có cùng id.
• Khi thực hiện hoạt động truy vấn: Nếu hai phần tử có cùng id, điều đó có nghĩa là chúng thuộc cùng một tập hợp; nếu hai phần tử có id khác nhau, điều đó có nghĩa là chúng không thuộc cùng một tập hợp.

Dưới đây là một ví dụ để minh họa: Chúng ta sử dụng một mảng để biểu diễn các phần tử trong tập hợp {0}, {1}, {2}, {3}, {4}, {5}, {6}, {7}. Khi khởi tạo, mảng sẽ có dạng như hình dưới đây. Từ hình dưới đây, chúng ta có thể thấy rằng id của mỗi phần tử là duy nhất, đại diện cho việc mỗi phần tử độc lập thuộc một tập hợp.

20220505145234.png

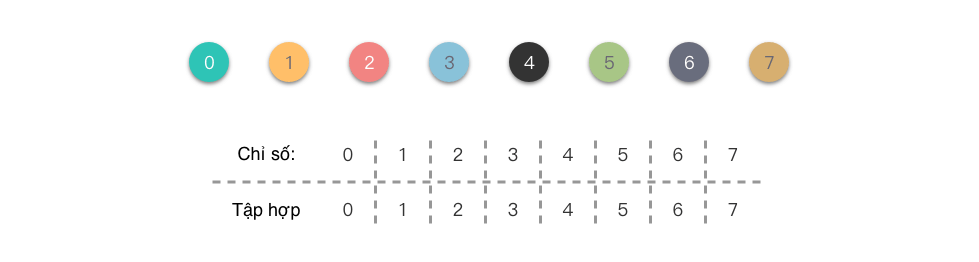
Sau khi thực hiện một loạt các hoạt động hợp nhất, ví dụ như hợp nhất thành {0}, {1, 2, 3}, {4}, {5, 6}, {7}, kết quả của hoạt động hợp nhất được thể hiện trong hình dưới đây. Từ hình dưới đây, chúng ta có thể thấy rằng id của các phần tử có chỉ số 1, 2, 3 là giống nhau, cho thấy ba phần tử này thuộc cùng một tập hợp. Tương tự, phần tử có chỉ số 5 và 6 cũng thuộc cùng một tập hợp.

20220505145302.png

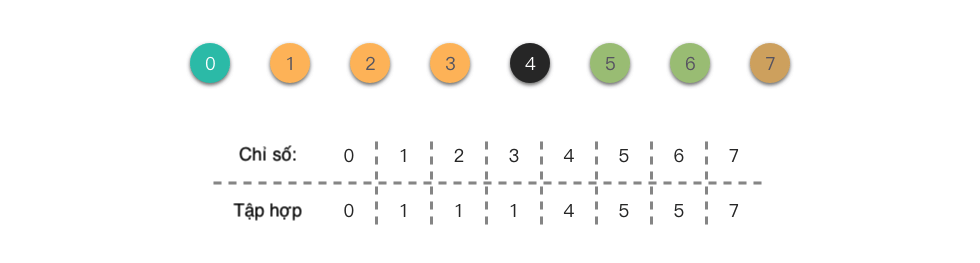
Trong phương pháp triển khai "truy vấn nhanh", độ phức tạp thời gian của mỗi hoạt động truy vấn là $O(1)$, trong khi độ phức tạp thời gian của mỗi hoạt động hợp nhất là $O(n)$ (mỗi hoạt động hợp nhất đều phải duyệt qua toàn bộ mảng). Hai độ phức tạp thời gian này khác biệt rất lớn, hoàn toàn hy sinh hiệu suất của hoạt động hợp nhất. Do đó, phương pháp triển khai Union-Find này không được sử dụng phổ biến.

• Dưới đây là mã nguồn triển khai Union-Find bằng phương pháp "truy vấn nhanh":

class UnionFind:
    def __init__(self, n):                          # Khởi tạo: Gán mỗi phần tử trong tập hợp một số hiệu tương ứng với chỉ số mảng
        self.ids = [i for i in range(n)]

    def find(self, x):                              # Truy vấn: Tìm kiếm số hiệu tập hợp của phần tử
        return self.ids[x]

    def union(self, x, y):                          # Hợp nhất: Thay đổi số hiệu tập hợp của tất cả các phần tử trong tập hợp
        x_id = self.find(x)
        y_id = self.find(y)
        
        if x_id == y_id:                            # x và y đã thuộc cùng một tập hợp
            return False
        
        for i in range(len(self.ids)):              # Thay đổi số hiệu tập hợp của hai tập hợp để trở thành giống nhau
            if self.ids[i] == y_id:
                self.ids[i] = x_id
        return True

    def is_connected(self, x, y):                   # Truy vấn: Kiểm tra xem x và y có thuộc cùng một tập hợp hay không
        return self.find(x) == self.find(y)

1.2.2 Hợp nhất nhanh: Triển khai dựa trên cây

Vì phương pháp triển khai "truy vấn nhanh" trong Union-Find có hiệu suất hợp nhất thấp, vì vậy hiện nay chúng ta tập trung vào việc cải thiện hiệu suất của hoạt động hợp nhất.

Khi triển khai Union-Find bằng phương pháp "hợp nhất nhanh", chúng ta có thể sử dụng "một cây (hoặc nhiều cây)" để lưu trữ tất cả các tập hợp. Mỗi cây đại diện cho một tập hợp, trong đó mỗi nút trên cây là một phần tử và nút gốc của cây là phần tử đại diện cho tập hợp đó.

Lưu ý: Khác với cấu trúc cây thông thường (nút cha trỏ đến nút con), trong Union-Find triển khai dựa trên cây, các nút con trỏ đến nút cha.

Lúc này, chúng ta vẫn có thể sử dụng một mảng fa để lưu trữ cây này. Chúng ta sử dụng fa[x] để lưu trữ số hiệu của nút cha của phần tử x, đại diện cho việc nút phần tử x trỏ đến nút cha fa[x].

Khi khởi tạo, giá trị fa[x] được gán bằng chỉ số mảng x. Khi thực hiện hoạt động hợp nhất, chúng ta chỉ cần kết nối nút gốc của một cây với nút gốc của cây khác (fa[root1] = root2). Khi thực hiện hoạt động truy vấn, chúng ta chỉ cần kiểm tra xem hai phần tử có cùng nút gốc hay không để xác định xem chúng có thuộc cùng một tập hợp hay không.

Tóm lại, chúng ta có thể thực hiện các hoạt động sau trên mảng fa để triển khai Union-Find:

• Khi khởi tạo: Gán mỗi phần tử trong tập hợp một số hiệu tương ứng với chỉ số mảng fa. Nút gốc của mỗi cây có số hiệu tập hợp khác nhau, đại diện cho việc mỗi phần tử độc lập thuộc một tập hợp.
• Khi thực hiện hoạt động hợp nhất: Chúng ta chỉ cần kết nối nút gốc của một cây với nút gốc của cây khác (fa[root1] = root2). Sau khi hợp nhất, tất cả các phần tử trong tập hợp sau hợp nhất đều có cùng nút gốc.
• Khi thực hiện hoạt động truy vấn: Chúng ta chỉ cần kiểm tra xem hai phần tử có cùng nút gốc hay không để xác định xem chúng có thuộc cùng một tập hợp hay không.

Dưới đây là một ví dụ để minh họa: Chúng ta sử dụng một mảng để biểu diễn các phần tử trong tập hợp {0}, {1}, {2}, {3}, {4}, {5}, {6}, {7}. Khi khởi tạo, mảng sẽ có dạng như hình dưới đây. Từ hình dưới đây, chúng ta có thể thấy rằng nút gốc của mỗi cây có số hiệu tập hợp khác nhau, đại diện cho việc mỗi phần tử độc lập thuộc một tập hợp.

20220507112934.png

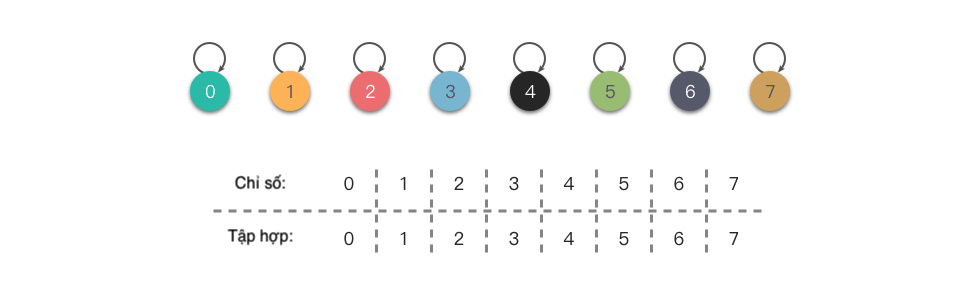
Sau khi thực hiện một loạt các hoạt động hợp nhất, ví dụ như union(4, 5)、union(6, 7)、union(4, 7) thì kết quả của hoạt động hợp nhất được thể hiện trong hình dưới đây. Từ hình dưới đây, chúng ta có thể thấy rằng fa[4] == fa[5] == fa[6] == fa[fa[7]] tức là nút gốc của các phần tử có chỉ số 4, 5, 6 là giống nhau, cho thấy ba phần tử này thuộc cùng một tập hợp. Tương tự, phần tử có chỉ số 7 cũng thuộc cùng một tập hợp.

20220507142647.png

Trong phương pháp triển khai "hợp nhất nhanh", độ phức tạp thời gian của mỗi hoạt động truy vấn là $O(h)$, trong đó $h$ là chiều cao của cây. Độ phức tạp thời gian của mỗi hoạt động hợp nhất là $O(1)$, vì chúng ta chỉ cần thay đổi nút gốc của một cây để kết nối hai cây. Vì vậy, phương pháp triển khai Union-Find này được sử dụng phổ biến hơn.

• Dưới đây là mã nguồn triển khai Union-Find bằng phương pháp "hợp nhất nhanh":

class UnionFind:
    def __init__(self, n):                          # Khởi tạo: Gán mỗi phần tử trong tập hợp một số hiệu tương ứng với chỉ số mảng fa
        self.fa = [i for i in range(n)]

    def find(self, x):                              # Truy vấn: Tìm kiếm số hiệu tập hợp của nút gốc của phần tử
        while self.fa[x] != x:                      # Duyệt ngược từ phần tử x đến nút gốc của cây
            x = self.fa[x]
        return x                                    # Trả về số hiệu tập hợp của nút gốc của phần tử

    def union(self, x, y):                          # Hợp nhất: Kết nối nút gốc của một cây với nút gốc của cây khác
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:                        # Nút gốc của x và y có cùng số hiệu tập hợp, tức là x và y đã thuộc cùng một tập hợp
            return False
        self.fa[root_x] = root_y                    # Kết nối nút gốc của x với nút gốc của y, trở thành con của nút gốc của y
        return True

    def is_connected(self, x, y):                   # Truy vấn: Kiểm tra xem x và y có thuộc cùng một tập hợp hay không
        return self.find(x) == self.find(y)

2. Nén đường dẫn

Khi tập hợp lớn hoặc cây không cân bằng, việc triển khai Union-Find bằng phương pháp "hợp nhất nhanh" trong mã nguồn trên có hiệu suất kém, trong trường hợp xấu nhất, cây có thể biến thành một chuỗi duy nhất và độ phức tạp thời gian truy vấn một lần là $O(n)$. Tình huống xấu nhất của Union-Find được minh họa trong hình dưới đây.

20220507172300.png

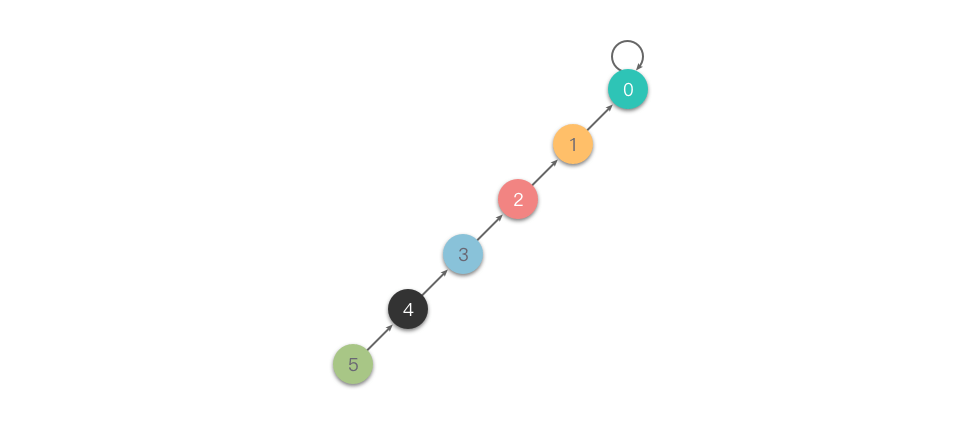
Để tránh tình huống xấu nhất này, một cách tối ưu phổ biến là "nén đường dẫn".

Nén đường dẫn (Path Compression): Trong quá trình tìm kiếm từ dưới lên đến nút gốc, nếu nút được truy cập không phải là nút gốc, chúng ta có thể di chuyển nút này lên một cấp độ để giảm xếp hạng của cây. Quá trình này được gọi là nén đường dẫn.

Nén đường dẫn có hai phương pháp: "nén đường dẫn qua đời" và "nén đường dẫn hoàn toàn".

2.1 Nén đường dẫn qua thế hệ

Nén đường dẫn qua thế hệ (Path Halving): Trong quá trình tìm kiếm, sau mỗi bước tìm kiếm, chúng ta di chuyển nút hiện tại trực tiếp đến ông nội của nó (nút cha của nút cha), từ đó giảm xếp hạng của cây.

Dưới đây là một ví dụ về "nén đường dẫn qua thế hệ".

20220509113955.png

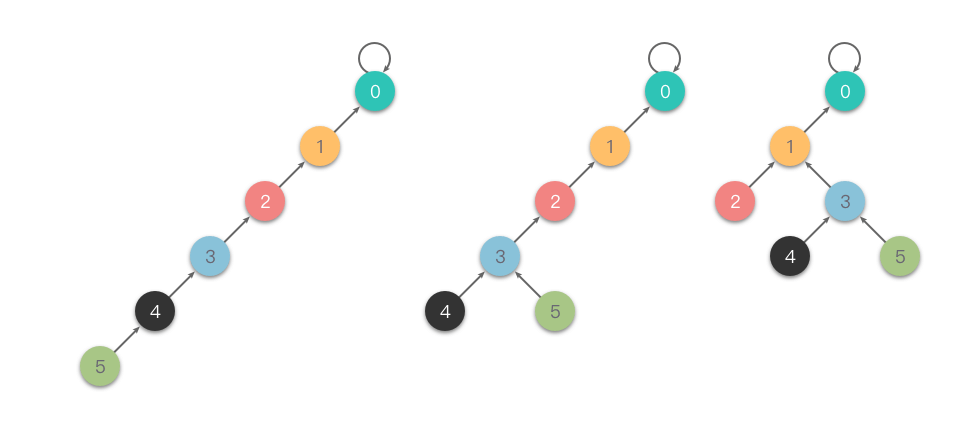
• Mã nguồn tìm kiếm với nén đường dẫn qua thế hệ như sau:

def find(self, x):                              # Tìm kiếm: Tìm kiếm số hiệu tập hợp của nút gốc của phần tử
    while self.fa[x] != x:                      # Duyệt ngược từ phần tử x đến nút gốc của cây
        self.fa[x] = self.fa[self.fa[x]]        # Nén đường dẫn qua đời
        x = self.fa[x]
    return x                                    # Trả về số hiệu tập hợp của nút gốc của phần tử

2.2 Nén đường dẫn hoàn toàn

Nén đường dẫn hoàn toàn (Full Path Compression): Trong quá trình tìm kiếm, chúng ta đặt tất cả các nút trên đường từ nút được tìm kiếm đến nút gốc trực tiếp trỏ đến nút gốc, từ đó giảm xếp hạng của cây. Nghĩa là, khi chúng ta tìm kiếm một nút, chúng ta cập nhật tất cả các nút trên đường dẫn đến nút gốc để trỏ trực tiếp đến nút gốc.

So với "nén đường dẫn qua thế hệ", "nén đường dẫn hoàn toàn" nén đường dẫn một cách toàn diện hơn. Dưới đây là một ví dụ về "nén đường dẫn hoàn toàn".

20220507174723.png

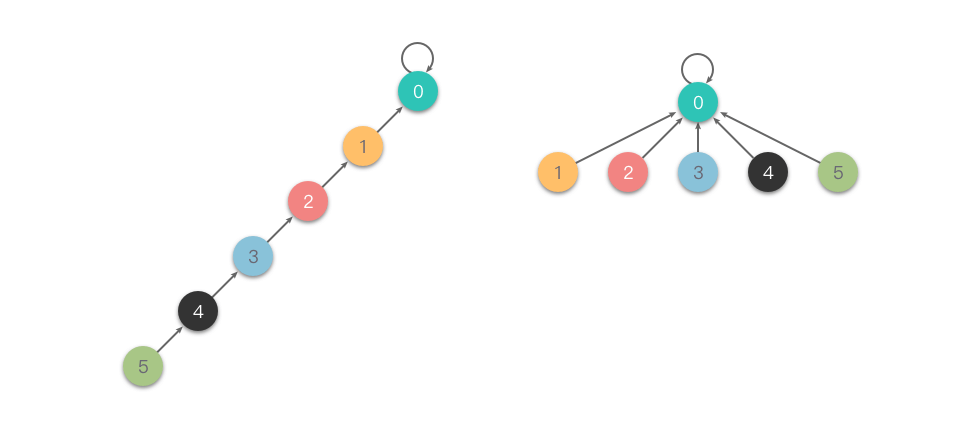
• Mã nguồn tìm kiếm với nén đường dẫn hoàn toàn như sau:

def find(self, x):                              # Tìm kiếm: Tìm kiếm số hiệu tập hợp của nút gốc của phần tử
    if self.fa[x] != x:                         # Duyệt ngược từ phần tử x đến nút gốc của cây
        self.fa[x] = self.find(self.fa[x])      # Tối ưu nén đường dẫn hoàn toàn
    return self.fa[x]

3. Hợp nhất theo xếp hạng

Vì việc nén đường dẫn chỉ được thực hiện trong quá trình truy vấn và chỉ nén một đường dẫn trên một cây, nên cấu trúc cuối cùng của hợp đồng cũng có thể phức tạp. Để tránh tình huống này, một cách tối ưu khác là "Hợp nhất theo xếp hạng".

Hợp nhất theo xếp hạng (Union By Rank): Trong mỗi lần thực hiện phép Hợp nhất, chúng ta luôn đảm bảo rằng nút gốc với "thứ bậc" nhỏ hơn sẽ trỏ đến nút gốc với "thứ bậc" lớn hơn.

Ở đây, "thứ bậc" có hai cách định nghĩa, một cách định nghĩa là xếp hạng của cây; cách định nghĩa khác là kích thước của cây (tức số lượng nút trong tập hợp). Bất kể cách định nghĩa nào được chọn, thứ bậc của tập hợp được ghi lại trên nút gốc của cây.

Hợp nhất theo xếp hạng cũng có hai cách thực hiện: một cách gọi là "Hợp nhất theo xếp hạng", cách thứ hai gọi là "Hợp nhất theo kích thước".

3.1 Hợp nhất theo xếp hạng

Hợp nhất theo xếp hạng (Union By Rank): Trong mỗi lần thực hiện Hợp nhất, chúng ta sẽ gán nút gốc có xếp hạng nhỏ hơn vào nút gốc có xếp hạng lớn hơn.

Chúng ta sử dụng một mảng rank để lưu xếp hạng của mỗi nút gốc (nếu không phải là nút gốc, giá trị rank tương đương với xếp hạng của cây con có nút đó là nút gốc).

Ban đầu, ta gán giá trị rank của tất cả các phần tử là 1. Trong quá trình Hợp nhất, so sánh hai nút gốc và gán nút gốc có giá trị rank nhỏ hơn vào nút gốc có giá trị rank lớn hơn để thực hiện Hợp nhất.

Dưới đây là một ví dụ về "Hợp nhất theo xếp hạng".

20220509094655.png

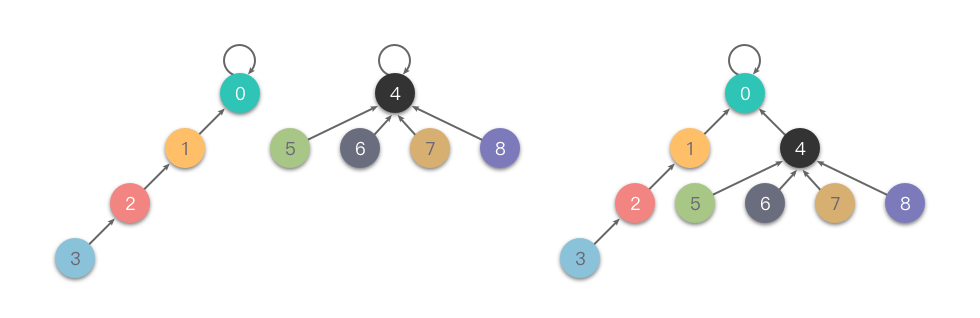
• Code thực hiện "Hợp nhất theo xếp hạng" như sau:

class UnionFind:
    def __init__(self, n):                          # Khởi tạo
        self.fa = [i for i in range(n)]             # Gán số hiệu tập hợp của mỗi phần tử là chỉ số của mảng fa
        self.rank = [1 for i in range(n)]           # Gán xếp hạng của mỗi phần tử là 1
    
    def find(self, x):                              # Phương thức tìm số hiệu tập hợp của nút gốc
        while self.fa[x] != x:                      # Tìm đệ quy nút cha của phần tử, cho đến khi tìm được nút gốc
            self.fa[x] = self.fa[self.fa[x]]        # Nén đường dẫn
            x = self.fa[x]
        return x                                    # Trả về số hiệu tập hợp của nút gốc

    def union(self, x, y):                          # Thực hiện Hợp nhất: gán nút gốc của một tập hợp vào nút gốc của tập hợp khác
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:                        # Hai nút có cùng số hiệu tập hợp, tức là đã thuộc cùng một tập hợp
            return False
        
        if self.rank[root_x] < self.rank[root_y]:   # xếp hạng của nút gốc của x nhỏ hơn xếp hạng của nút gốc của y
            self.fa[root_x] = root_y                # Gán nút gốc của x vào nút gốc của y, trở thành con của nút gốc của y
        elif self.rank[root_y] > self.rank[root_y]: # xếp hạng của nút gốc của x lớn hơn xếp hạng của nút gốc của y
            self.fa[root_y] = root_x                # Gán nút gốc của y vào nút gốc của x, trở thành con của nút gốc của x
        else:                                       # xếp hạng của nút gốc của x bằng xếp hạng của nút gốc của y
            self.fa[root_x] = root_y                # Hợp nhất vào bất kỳ bên nào cũng được
            rank[y] += 1                            # Vì xếp hạng bằng nhau, cây bị hợp nhất sẽ tăng thêm 1 xếp hạng
        return True

    def is_connected(self, x, y):                   # Phương thức kiểm tra: kiểm tra xem x và y có thuộc cùng một tập hợp không
        return self.find(x) == self.find(y)

3.2 Hợp nhất theo kích thước

Hợp nhất theo kích thước (Union By Size): Ở đây, kích thước được hiểu là số lượng nút trong tập hợp. Trong mỗi lần thực hiện hợp nhất, chúng ta sẽ gán nút gốc có kích thước nhỏ hơn vào nút gốc có kích thước lớn hơn.

Chúng ta sử dụng một mảng size để lưu kích thước của mỗi nút gốc (nếu không phải là nút gốc, giá trị size tương đương với số lượng nút trong cây con có nút đó là nút gốc).

Ban đầu, ta gán giá trị size của tất cả các phần tử là 1. Trong quá trình Hợp nhất, so sánh hai nút gốc và gán nút gốc có giá trị size nhỏ hơn vào nút gốc có giá trị size lớn hơn để thực hiện Hợp nhất.

Dưới đây là một ví dụ về "Hợp nhất theo kích thước".

20220509094635.png

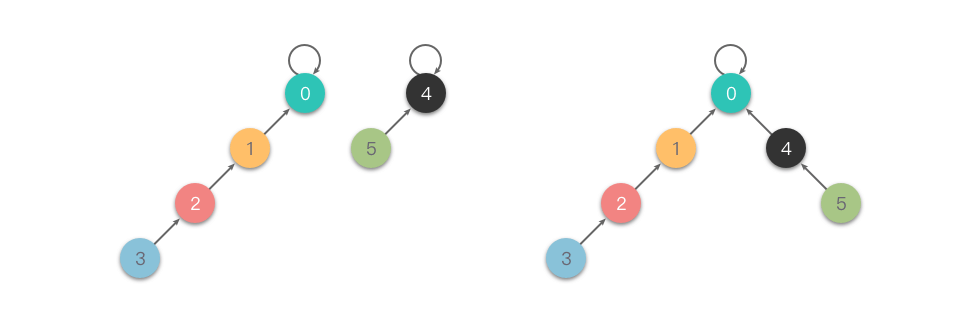
• Code thực hiện "Hợp nhất theo kích thước" như sau:

class UnionFind:
    def __init__(self, n):                          # Khởi tạo
        self.fa = [i for i in range(n)]             # Gán số hiệu tập hợp của mỗi phần tử là chỉ số của mảng fa
        self.size = [1 for i in range(n)]           # Gán kích thước của mỗi phần tử là 1
    
    def find(self, x):                              # Phương thức tìm số hiệu tập hợp của nút gốc
        while self.fa[x] != x:                      # Tìm đệ quy nút cha của phần tử, cho đến khi tìm được nút gốc
            self.fa[x] = self.fa[self.fa[x]]        # Nén đường dẫn
            x = self.fa[x]
        return x                                    # Trả về số hiệu tập hợp của nút gốc

    def union(self, x, y):                          # Thực hiện Hợp nhất: gán nút gốc của một tập hợp vào nút gốc của tập hợp khác
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:                        # Hai nút có cùng số hiệu tập hợp, tức là đã thuộc cùng một tập hợp
            return False
        
        if self.size[root_x] < self.size[root_y]:   # Kích thước của nút gốc của x nhỏ hơn kích thước của nút gốc của y
            self.fa[root_x] = root_y                # Gán nút gốc của x vào nút gốc của y, trở thành con của nút gốc của y
            self.size[root_y] += self.size[root_x]  # Kích thước của nút gốc của y tăng thêm kích thước của nút gốc của x
        elif self.size[root_x] > self.size[root_y]: # Kích thước của nút gốc của x lớn hơn kích thước của nút gốc của y
            self.fa[root_y] = root_x                # Gán nút gốc của y vào nút gốc của x, trở thành con của nút gốc của x
            self.size[root_x] += self.size[root_y]  # Kích thước của nút gốc của x tăng thêm kích thước của nút gốc của y
        else:                                       # Kích thước của nút gốc của x bằng kích thước của nút gốc của y
            self.fa[root_x] = root_y                # Hợp nhất vào bất kỳ bên nào cũng được
            self.size[root_y] += self.size[root_x]
            
        return True

    def is_connected(self, x, y):                   # Phương thức kiểm tra: kiểm tra xem x và y có thuộc cùng một tập hợp không
        return self.find(x) == self.find(y)

3.3 Lưu ý về Hợp nhất theo xếp hạng

Sau khi xem qua mã thực hiện "Hợp nhất theo xếp hạng" và "Hợp nhất theo kích thước", có thể có một câu hỏi: Tại sao trong quá trình nén đường dẫn, chúng ta không cập nhật giá trị rank hoặc size?

Thực tế, giá trị rank hoặc size trong mã không phản ánh chính xác xếp hạng thực tế hoặc số lượng phần tử trong tập hợp.

Điều này xảy ra vì khi chúng ta áp dụng nén đường dẫn vào mã, việc duy trì xếp hạng thực tế hoặc số lượng phần tử trong tập hợp trở nên khó khăn. Trong trường hợp này, giá trị rank hoặc size được sử dụng như một số chỉ số xếp hạng hiện tại của nút, chỉ được sử dụng trong quá trình so sánh hai cây để chọn cách Hợp nhất phù hợp.

Nói cách khác, chúng ta hoàn toàn có thể không biết xếp hạng cụ thể hoặc số lượng phần tử của mỗi nút, miễn là chúng ta đảm bảo rằng mối quan hệ xếp hạng hoặc số lượng phần tử giữa hai nút bất kỳ có thể được biểu diễn chính xác bằng giá trị rank hoặc size.

Và theo quá trình nén đường dẫn, giá trị rank hoặc size chỉ tăng lên và không thể giảm xuống dưới xếp hạng ban đầu của nút hoặc số lượng phần tử ít hơn của nút. Do đó, giá trị rank hoặc size là đủ để so sánh trọng số của hai nút và chọn cách Hợp nhất phù hợp.

4. Phân tích thuật toán Union Find

Đầu tiên, chúng ta hãy phân tích độ phức tạp về không gian của Union-Find. Trong code, chúng ta chủ yếu sử dụng mảng fa để lưu trữ các phần tử trong tập hợp. Nếu sử dụng tối ưu hóa "hợp nhất theo xếp hạng", chúng ta cũng sẽ sử dụng mảng rank hoặc mảng size để lưu trữ trọng số. Vì vậy, độ phức tạp về không gian phụ thuộc vào số lượng phần tử, và không khó để thấy rằng độ phức tạp về không gian là $O(n)$.

Trong trường hợp sử dụng cả "nén đường dẫn" và "hợp nhất theo xếp hạng", độ phức tạp thời gian của phép hợp nhất và phép tìm kiếm trong Union-Find có thể tiến gần đến $O(1)$. Độ phức tạp thời gian trong trường hợp xấu nhất là $O(m * \alpha(n))$. Ở đây, $m$ là số lần thực hiện phép hợp nhất và phép tìm kiếm, $\alpha(n)$ là một hàm ngược của hàm Ackerman, tăng rất chậm. Điều này có nghĩa rằng thời gian chạy trung bình của mỗi phép toán có thể coi là một hằng số rất nhỏ.

Tóm lại:

• Độ phức tạp về không gian của Union-Find: $O(n)$.
• Độ phức tạp thời gian của Union-Find: $O(m * \alpha(n))$.

5. Code hoàn chỉnh của Union-Find

Dựa trên kinh nghiệm học tập của bản thân và kinh nghiệm của các chuyên gia trên mạng, tôi sử dụng chiến lược của Union-Find như sau (chỉ để tham khảo): Sử dụng "nén đường dẫn" và thường không sử dụng "hợp nhất theo xếp hạng".

Lý do chọn cách này là để đảm bảo code đơn giản và dễ viết, đồng thời đạt được hiệu suất tốt. Nếu hiệu suất của cách viết này vẫn chưa đủ tốt, hãy xem xét việc sử dụng "hợp nhất theo xếp hạng".

Trong một số bài toán, chúng ta cũng có thể gặp trường hợp cần truy vấn số lượng tập hợp hoặc số lượng phần tử trong tập hợp, và có thể điều chỉnh code tương ứng theo yêu cầu cụ thể của bài toán.

• Code Union-Find sử dụng "nén đường dẫn" và không sử dụng "hợp nhất theo xếp hạng":

class UnionFind:
    def __init__(self, n):                          # Khởi tạo
        self.fa = [i for i in range(n)]             # Gán số hiệu tập hợp của mỗi phần tử bằng chỉ số mảng fa
    
    def find(self, x):                              # Phương thức tìm số hiệu tập hợp gốc của phần tử
        while self.fa[x] != x:                      # Tìm đệ quy phần tử cha cho đến khi tìm được tập hợp gốc
            self.fa[x] = self.fa[self.fa[x]]        # Nén đường dẫn
            x = self.fa[x]
        return x                                    # Trả về số hiệu tập hợp gốc của phần tử

    def union(self, x, y):                          # Phương thức hợp nhất: gán tập hợp gốc của một tập hợp vào tập hợp gốc của tập hợp khác
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:                        # Nếu số hiệu tập hợp gốc của x và y giống nhau, tức là x và y đã thuộc cùng một tập hợp
            return False
        
        self.fa[root_x] = root_y                    # Gán tập hợp gốc của x vào tập hợp gốc của y, làm cho x trở thành con của y
        return True

    def is_connected(self, x, y):                   # Phương thức truy vấn: kiểm tra x và y có thuộc cùng một tập hợp không
        return self.find(x) == self.find(y)

• Code Union-Find sử dụng "nén đường dẫn" và "hợp nhất theo xếp hạng":

class UnionFind:
    def __init__(self, n):                          # Khởi tạo
        self.fa = [i for i in range(n)]             # Gán số hiệu tập hợp của mỗi phần tử bằng chỉ số mảng fa
        self.rank = [1 for i in range(n)]           # Gán xếp hạng của mỗi phần tử bằng 1
    
    def find(self, x):                              # Phương thức tìm số hiệu tập hợp gốc của phần tử
        while self.fa[x] != x:                      # Tìm đệ quy phần tử cha cho đến khi tìm được tập hợp gốc
            self.fa[x] = self.fa[self.fa[x]]        # Nén đường dẫn
            x = self.fa[x]
        return x                                    # Trả về số hiệu tập hợp gốc của phần tử

    def union(self, x, y):                          # Phương thức hợp nhất: gán tập hợp gốc của một tập hợp vào tập hợp gốc của tập hợp khác
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:                        # Nếu số hiệu tập hợp gốc của x và y giống nhau, tức là x và y đã thuộc cùng một tập hợp
            return False
        
        if self.rank[root_x] < self.rank[root_y]:   # Nếu xếp hạng của tập hợp gốc của x nhỏ hơn xếp hạng của tập hợp gốc của y
            self.fa[root_x] = root_y                # Gán tập hợp gốc của x vào tập hợp gốc của y, làm cho x trở thành con của y
        elif self.rank[root_y] > self.rank[root_y]: # Nếu xếp hạng của tập hợp gốc của x lớn hơn xếp hạng của tập hợp gốc của y
            self.fa[root_y] = root_x                # Gán tập hợp gốc của y vào tập hợp gốc của x, làm cho y trở thành con của x
        else:                                       # Nếu xếp hạng của tập hợp gốc của x bằng xếp hạng của tập hợp gốc của y
            self.fa[root_x] = root_y                # Gán tập hợp gốc của x vào tập hợp gốc của y, làm cho x trở thành con của y
            self.rank[y] += 1                       # Vì xếp hạng bằng nhau, cây bị hợp nhất sẽ có xếp hạng tăng lên 1
        return True

    def is_connected(self, x, y):                   # Phương thức truy vấn: kiểm tra x và y có thuộc cùng một tập hợp không
        return self.find(x) == self.find(y)

6. Ứng dụng của Union-Find

Union-Find thường được sử dụng để giải quyết các vấn đề liên quan đến mối quan hệ giữa các phần tử khác nhau, chẳng hạn như xác định xem hai người có quan hệ họ hàng hay không, xem hai điểm có tồn tại ít nhất một đường đi kết nối hay không. Ngoài ra, nó cũng được sử dụng để đếm số lượng tập hợp, số lượng phần tử trong tập hợp, và nhiều ứng dụng khác.

6.1. Đáp ứng tính khả thi của phương trình

6.1.1. Liên kết đến bài toán

• 990. Satisfiability of Equality Equations

6.1.2. Tóm tắt đề bài

Mô tả: Cho một mảng các phương trình chuỗi, mỗi phương trình chuỗi equations[i] có độ dài 4 và có hai dạng sau: a==b hoặc a!=b. a và b là các chữ cái thường đại diện cho tên biến đơn chữ.

Yêu cầu: Xác định xem tất cả các phương trình chuỗi có thể đồng thời thỏa mãn hay không. Nếu có thể thỏa mãn, trả về True, ngược lại trả về False.

Giải thích:

• $1 \le equations.length \le 500$.
• $equations[i].length == 4$.
• $equations[i][0]$ và $equations[i][3]$ là các chữ cái thường.
• $equations[i][1]$ có thể là '=' hoặc '!'.
• $equations[i][2]$ là '='.

Ví dụ:

Input: ["a==b","b!=a"]
Output: False
Explanation: Nếu chúng ta gán a = 1 và b = 1, thì có thể thỏa mãn phương trình đầu tiên, nhưng không thể thỏa mãn phương trình thứ hai. Không có cách nào gán giá trị cho các biến sao cho cả hai phương trình đều thỏa mãn.

6.1.3. Ý tưởng giải quyết

Phương trình chuỗi chỉ có hai dạng == hoặc !=, ta có thể xem xét việc gom nhóm các biến bằng nhau vào cùng một tập hợp, sau đó kiểm tra xem hai biến trong mỗi phương trình không bằng nhau có thuộc cùng một thành phần liên thông hay không. Nếu có, tức là không thỏa mãn.

Điều này đòi hỏi sử dụng Union-Find, cụ thể như sau:

• Duyệt qua tất cả các phương trình ==, gom nhóm các đỉnh biến bên trái và bên phải của phương trình vào cùng một thành phần liên thông.
• Duyệt qua tất cả các phương trình !=, kiểm tra xem hai đỉnh biến của phương trình có thuộc cùng một thành phần liên thông hay không. Nếu có, trả về False, ngược lại tiếp tục duyệt. Nếu không có phương trình nào không thỏa mãn, trả về True.

6.1.4. Code

class UnionFind:
    def __init__(self, n):                          # Khởi tạo
        self.fa = [i for i in range(n)]             # Gán số hiệu tập hợp của mỗi phần tử bằng chỉ số mảng fa
    
    def find(self, x):                              # Phương thức tìm số hiệu tập hợp gốc của phần tử
        while self.fa[x] != x:                      # Tìm đệ quy phần tử cha cho đến khi tìm được tập hợp gốc
            self.fa[x] = self.fa[self.fa[x]]        # Nén đường dẫn
            x = self.fa[x]
        return x                                    # Trả về số hiệu tập hợp gốc của phần tử

    def union(self, x, y):                          # Phương thức hợp nhất: gán tập hợp gốc của một tập hợp vào tập hợp gốc của tập hợp khác
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:                        # Nếu số hiệu tập hợp gốc của x và y giống nhau, tức là x và y đã thuộc cùng một tập hợp
            return False
        
        self.fa[root_x] = root_y                    # Gán tập hợp gốc của x vào tập hợp gốc của y, làm cho x trở thành con của y
        return True

    def is_connected(self, x, y):                   # Phương thức truy vấn: kiểm tra x và y có thuộc cùng một tập hợp không
        return self.find(x) == self.find(y)

class Solution:
    def equationsPossible(self, equations: List[str]) -> bool:
        union_find = UnionFind(26)
        for equation in equations:
            if equation[1] == "=":
                index1 = ord(equation[0]) - 97
                index2 = ord(equation[3]) - 97
                union_find.union(index1, index2)

        for equation in equations:
            if equation[1] == "!":
                index1 = ord(equation[0]) - 97
                index2 = ord(equation[3]) - 97
                if union_find.is_connected(index1, index2):
                    return False
        return True

6.2 Số lượng tỉnh

6.2.1 Liên kết đến bài toán

• 547. Number of Provinces

6.2.2 Tóm tắt đề bài

Mô tả: Có n thành phố, một số thành phố có liên kết với nhau và một số không. Nếu thành phố a liên kết trực tiếp với thành phố b và thành phố b liên kết trực tiếp với thành phố c, thì thành phố a liên kết gián tiếp với thành phố c.

"Một tỉnh" được hình thành bởi một nhóm thành phố liên kết trực tiếp hoặc gián tiếp với nhau, không chứa bất kỳ thành phố nào không liên kết với nhóm.

Cho ma trận isConnected có kích thước n * n đại diện cho mối quan hệ liên kết giữa các thành phố. Trong đó, isConnected[i][j] = 1 nếu thành phố thứ i và thành phố thứ j liên kết trực tiếp, và isConnected[i][j] = 0 nếu không liên kết trực tiếp.

Yêu cầu: Dựa trên mối quan hệ thành phố đã cho, trả về số lượng "tỉnh".

Giải thích:

• $1 \le n \le 200$.
• $n == isConnected.length$.
• $n == isConnected[i].length$.
• $isConnected[i][j]$ là $1$ hoặc $0$.
• $isConnected[i][i] == 1$.
• $isConnected[i][j] == isConnected[j][i]$.

Ví dụ:

• Như hình dưới đây:

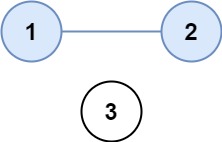
Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]]
Output: 2

6.2.3 Ý tưởng giải quyết

Cách tiếp cận cụ thể như sau:

• Duyệt qua ma trận isConnected. Nếu isConnected[i][j] = 1, kết nối nút i và nút j.
• Sau đó, xác định nút gốc của từng thành phố, rồi đếm số lượng nút gốc không trùng lặp, đó chính là số lượng "tỉnh".

6.2.4 Đoạn mã

class UnionFind:
    def __init__(self, n):                          # Khởi tạo
        self.fa = [i for i in range(n)]             # Gán số hiệu tập hợp của mỗi phần tử bằng chỉ số mảng fa
    
    def find(self, x):                              # Phương thức tìm số hiệu tập hợp gốc của phần tử
        while self.fa[x] != x:                      # Tìm đệ quy phần tử cha cho đến khi tìm được tập hợp gốc
            self.fa[x] = self.fa[self.fa[x]]        # Nén đường dẫn
            x = self.fa[x]
        return x                                    # Trả về số hiệu tập hợp gốc của phần tử

    def union(self, x, y):                          # Phương thức hợp nhất: gán tập hợp gốc của một tập hợp vào tập hợp gốc của tập hợp khác
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:                        # Nếu số hiệu tập hợp gốc của x và y giống nhau, tức là x và y đã thuộc cùng một tập hợp
            return False
        self.fa[root_x] = root_y                    # Gán tập hợp gốc của x vào tập hợp gốc của y, làm cho x trở thành con của y
        return True

    def is_connected(self, x, y):                   # Phương thức truy vấn: kiểm tra x và y có thuộc cùng một tập hợp không
        return self.find(x) == self.find(y)

class Solution:
    def findCircleNum(self, isConnected: List[List[int]]) -> int:
        size = len(isConnected)
        union_find = UnionFind(size)
        for i in range(size):
            for j in range(i + 1, size):
                if isConnected[i][j] == 1:
                    union_find.union(i, j)

        res = set()
        for i in range(size):
            res.add(union_find.find(i))
        return len(res)