Binary Search Tree
1. Giới thiệu về cây tìm kiếm nhị phân
Cây tìm kiếm nhị phân (Binary Search Tree) là một loại cây nhị phân đặc biệt, còn được gọi là cây tìm kiếm, cây sắp xếp nhị phân hoặc cây nhị phân tìm kiếm. Nó là một cây rỗng hoặc một cây nhị phân có các thuộc tính sau:
- Nếu cây con trái của một nút không rỗng, thì tất cả các giá trị trong cây con trái đó đều nhỏ hơn giá trị của nút đó.
- Nếu cây con phải của một nút không rỗng, thì tất cả các giá trị trong cây con phải đó đều lớn hơn giá trị của nút đó.
- Cả cây con trái và cây con phải của một nút đều là cây tìm kiếm nhị phân.
Như hình dưới đây, ba cây này đều là cây tìm kiếm nhị phân.
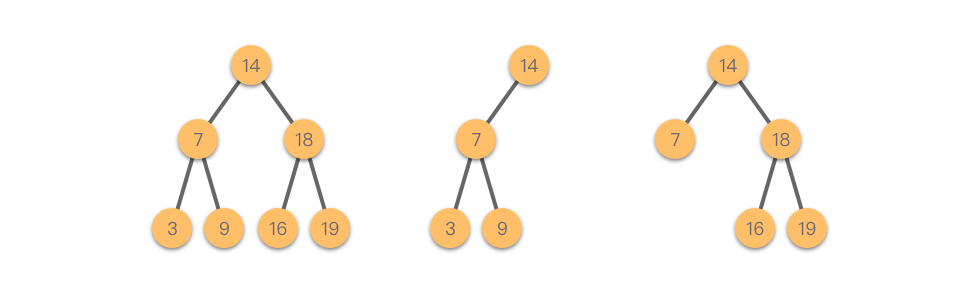
Cây nhị phân có một đặc điểm, đó là: giá trị của nút con bên trái < giá trị của nút gốc < giá trị của nút con bên phải.
Dựa trên đặc điểm này, khi thực hiện duyệt cây theo thứ tự trung tố (inorder), chúng ta sẽ thu được một dãy số tăng dần. Ví dụ, dãy số thu được từ việc duyệt cây tìm kiếm nhị phân dưới đây.
2. Tìm kiếm trong cây tìm kiếm nhị phân
Tìm kiếm trong cây tìm kiếm nhị phân: Tìm kiếm nút có giá trị
valtrong cây tìm kiếm nhị phân.
2.1 Các bước thực hiện thuật toán tìm kiếm trong cây tìm kiếm nhị phân
Theo định nghĩa của cây tìm kiếm nhị phân, khi tìm kiếm một phần tử, chúng ta chỉ cần xác định xem phải đi sang trái hay phải đi sang phải dựa trên giá trị của nút gốc. Điều này giúp thu hẹp phạm vi tìm kiếm ở mỗi bước, từ đó tăng hiệu suất tìm kiếm. Các bước tìm kiếm trong cây nhị phân như sau:
- Nếu cây tìm kiếm nhị phân rỗng, tìm kiếm thất bại, kết thúc tìm kiếm và trả về con trỏ rỗng
None. - Nếu cây tìm kiếm nhị phân không rỗng, so sánh giá trị cần tìm
valvới giá trị của nút gốcroot.val:- Nếu
val == root.val, tìm kiếm thành công, kết thúc tìm kiếm và trả về nút được tìm thấy. - Nếu
val < root.val, tiếp tục tìm kiếm trong cây con trái. - Nếu
val > root.val, tiếp tục tìm kiếm trong cây con phải.
- Nếu
2.2 Cài đặt tìm kiếm trong cây tìm kiếm nhị phân
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def searchBST(self, root: TreeNode, val: int) -> TreeNode:
if not root:
return None
if val == root.val:
return root
elif val < root.val:
return self.searchBST(root.left, val)
else:
return self.searchBST(root.right, val)2.3 Phân tích độ phức tạp của thuật toán tìm kiếm trong cây tìm kiếm nhị phân
- Độ phức tạp của thuật toán tìm kiếm trong cây tìm kiếm nhị phân phụ thuộc vào hình dạng của cây.
- Trong trường hợp tốt nhất, hình dạng của cây tìm kiếm nhị phân tương tự với cây quyết định nhị phân của tìm kiếm nhị phân. Mỗi lần tìm kiếm, phạm vi tìm kiếm được thu nhỏ đi một nửa. Đường dẫn tìm kiếm tối đa từ nút gốc đến nút lá, số lần so sánh tối đa là chiều cao của cây . Trong trường hợp tốt nhất, độ phức tạp tìm kiếm là .
- Trong trường hợp xấu nhất, hình dạng của cây tìm kiếm nhị phân là một cây con, có nghĩa là chỉ có cây con trái hoặc cây con phải. Mỗi lần tìm kiếm, phạm vi tìm kiếm được thu nhỏ xuống còn , trở thành tìm kiếm tuần tự. Trong trường hợp xấu nhất, độ phức tạp tìm kiếm là .
- Trong trường hợp trung bình, độ dài trung bình của tìm kiếm là . Vì vậy, độ phức tạp trung bình của tìm kiếm trong cây tìm kiếm nhị phân là .
3. Chèn vào cây tìm kiếm nhị phân
Chèn vào cây tìm kiếm nhị phân: Chèn một nút có giá trị
valvào cây tìm kiếm nhị phân (giả sử cây tìm kiếm nhị phân hiện tại không chứa nút có giá trịval).
3.1 Các bước thực hiện thuật toán chèn vào cây tìm kiếm nhị phân
Thủ tục chèn nút vào cây tìm kiếm nhị phân tương tự như thuật toán tìm kiếm. Các bước cụ thể như sau:
- Nếu cây tìm kiếm nhị phân rỗng, tạo một nút mới với giá trị
valvà đặt nút mới này làm nút gốc của cây. - Nếu cây tìm kiếm nhị phân không rỗng, so sánh giá trị cần chèn
valvới giá trị của nút gốcroot.val:- Nếu
val < root.val, tiếp tục chèn vào cây con trái. - Nếu
val > root.val, tiếp tục chèn vào cây con phải.
- Nếu
3.2 Cài đặt chèn vào cây tìm kiếm nhị phân
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
if root == None:
return TreeNode(val)
if val < root.val:
root.left = self.insertIntoBST(root.left, val)
if val > root.val:
root.right = self.insertIntoBST(root.right, val)
return root3.3 Phân tích độ phức tạp của thuật toán chèn vào cây tìm kiếm nhị phân
- Độ phức tạp của thuật toán chèn vào cây tìm kiếm nhị phân phụ thuộc vào hình dạng của cây.
- Trong trường hợp tốt nhất, hình dạng của cây tìm kiếm nhị phân tương tự với cây quyết định nhị phân của tìm kiếm nhị phân. Mỗi lần chèn, phạm vi chèn được thu nhỏ đi một nửa. Đường dẫn chèn tối đa từ nút gốc đến nút lá, số lần so sánh tối đa là chiều cao của cây . Trong trường hợp tốt nhất, độ phức tạp chèn là .
- Trong trường hợp xấu nhất, hình dạng của cây tìm kiếm nhị phân là một cây con, có nghĩa là chỉ có cây con trái hoặc cây con phải. Mỗi lần chèn, phạm vi chèn vẫn là , trở thành chèn tuần tự. Trong trường hợp xấu nhất, độ phức tạp chèn là .
- Trong trường hợp trung bình, độ dài trung bình của chèn là . Vì vậy, độ phức tạp trung bình của chèn vào cây tìm kiếm nhị phân là .
4. Tạo cây tìm kiếm nhị phân
Tạo cây tìm kiếm nhị phân: Tạo cây tìm kiếm nhị phân dựa trên giá trị của các phần tử trong một mảng.
4.1 Các bước thực hiện tạo cây tìm kiếm nhị phân
Thao tác tạo cây tìm kiếm nhị phân bắt đầu từ cây rỗng, sau đó thực hiện lần lượt các thao tác chèn để tạo cây tìm kiếm nhị phân từ mảng đã cho. Các bước thực hiện cụ thể như sau:
- Khởi tạo cây tìm kiếm nhị phân rỗng.
- Duyệt qua các phần tử trong mảng và chèn giá trị
nums[i]vào cây tìm kiếm nhị phân. - Sau khi chèn tất cả các phần tử trong mảng vào cây tìm kiếm nhị phân, trả về nút gốc của cây tìm kiếm nhị phân.
4.2 Cài đặt tạo cây tìm kiếm nhị phân
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
if root == None:
return TreeNode(val)
if val < root.val:
root.left = self.insertIntoBST(root.left, val)
if val > root.val:
root.right = self.insertIntoBST(root.right, val)
return root
def buildBST(self, nums) -> TreeNode:
root = TreeNode(val)
for num in nums:
self.insertIntoBST(root, num)
return root5. Xoá nút cây tìm kiếm nhị phân
Xoá nút cây tìm kiếm nhị phân: Xóa nút có giá trị
valtrong cây tìm kiếm nhị phân.
5.1 Các bước thực hiện Xoá nút cây tìm kiếm nhị phân
Để xóa một phần tử trong cây tìm kiếm nhị phân, trước tiên phải tìm ra nút cần xóa, sau đó thực hiện thao tác xóa. Tùy thuộc vào vị trí của nút cần xóa, có thể chia thành 3 trường hợp khác nhau:
- Cây con trái của nút cần xóa là rỗng. Khi đó, cây con phải sẽ thay thế vị trí của nút cần xóa.
- Cây con phải của nút cần xóa là rỗng. Khi đó, cây con trái sẽ thay thế vị trí của nút cần xóa.
- Cả cây con trái và cây con phải của nút cần xóa đều không rỗng. Trong trường hợp này, để duy trì tính chất của cây tìm kiếm nhị phân, ta có thể sử dụng nút trước đó (hoặc nút kế tiếp) của nút cần xóa để thay thế vị trí của nút cần xóa.
Các bước thực hiện Xoá nút cây tìm kiếm nhị phân như sau:
- Nếu nút hiện tại là rỗng, trả về nút hiện tại.
- Nếu giá trị của nút hiện tại lớn hơn
val, thực hiện đệ quy để tìm và xóa trong cây con trái, sau đó cập nhậtroot.left. - Nếu giá trị của nút hiện tại nhỏ hơn
val, thực hiện đệ quy để tìm và xóa trong cây con phải, sau đó cập nhậtroot.right. - Nếu giá trị của nút hiện tại bằng
val, nút hiện tại là nút cần xóa.- Nếu cây con trái của nút hiện tại là rỗng, trả về cây con phải để thay thế vị trí của nút cần xóa.
- Nếu cây con phải của nút hiện tại là rỗng, trả về cây con trái để thay thế vị trí của nút cần xóa.
- Nếu cả cây con trái và cây con phải của nút hiện tại đều không rỗng, tìm nút trái nhất trong cây con phải và chuyển cây con trái của nút hiện tại vào vị trí đó, sau đó trả về cây con phải để thay thế vị trí của nút cần xóa.
5.2 Cài đặt Xoá nút cây tìm kiếm nhị phân
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def deleteNode(self, root: TreeNode, val: int) -> TreeNode:
if not root:
return root
if root.val > val:
root.left = self.deleteNode(root.left, val)
return root
elif root.val < val:
root.right = self.deleteNode(root.right, val)
return root
else:
if not root.left:
return root.right
elif not root.right:
return root.left
else:
curr = root.right
while curr.left:
curr = curr.left
curr.left = root.left
return root.right