Skip to main content

Monotone Stack

Hung NguyenAbout 13 mindsadata-structuredsadata-structure

1. Giới thiệu về ngăn xếp đơn điệu

Ngăn xếp đơn điệu (Monotone Stack): Là một loại ngăn xếp đặc biệt. Dựa trên quy tắc "đẩy vào trước, lấy ra sau" của ngăn xếp, yêu cầu "từ đỉnh ngăn xếp đến đáy ngăn xếp các phần tử phải tăng dần (hoặc giảm dần)". Ngăn xếp có các phần tử từ đỉnh đến đáy tăng dần được gọi là "ngăn xếp tăng dần". Ngăn xếp có các phần tử từ đỉnh đến đáy giảm dần được gọi là "ngăn xếp giảm dần".

Lưu ý: Đây là định nghĩa theo thứ tự từ "đỉnh ngăn xếp" đến "đáy ngăn xếp". Một số bài viết có thể định nghĩa ngược lại. Trong bài viết này, chúng ta sẽ sử dụng thứ tự từ "đỉnh ngăn xếp" đến "đáy ngăn xếp" để mô tả ngăn xếp đơn điệu.

1.1 Ngăn xếp tăng dần

Ngăn xếp tăng dần: Chỉ có các phần tử nhỏ hơn phần tử đỉnh ngăn xếp mới có thể được đẩy vào ngăn xếp, nếu không, cần lấy ra các phần tử trong ngăn xếp nhỏ hơn hoặc bằng phần tử hiện tại trước khi đẩy phần tử hiện tại vào ngăn xếp.

Điều này đảm bảo rằng: trong ngăn xếp chỉ chứa các giá trị lớn hơn phần tử hiện tại và các phần tử từ đỉnh đến đáy ngăn xếp tăng dần.

Quá trình đẩy vào và lấy ra của ngăn xếp tăng dần như sau:

  • Giả sử phần tử hiện tại cần đẩy vào là x, nếu x nhỏ hơn phần tử đỉnh ngăn xếp, thì đẩy x vào ngăn xếp.
  • Ngược lại, bắt đầu từ đỉnh ngăn xếp, lấy ra các phần tử trong ngăn xếp lớn hơn x hoặc bằng x cho đến khi gặp phần tử nhỏ hơn x, sau đó đẩy x vào ngăn xếp.

Dưới đây, chúng ta sẽ lấy một ví dụ với mảng [2, 7, 5, 4, 6, 3, 4, 2] để mô phỏng quá trình đẩy vào và lấy ra của "ngăn xếp tăng dần". Quá trình cụ thể như sau:

  • Mảng: [2, 7, 5, 4, 6, 3, 4, 2], thứ tự duyệt từ trái sang phải.
Bước thứ iPhần tử cần đẩy vàoThao tácKết quả (từ trái sang phải)Ý nghĩa
12Đẩy 2 vào ngăn xếp[2]Không có phần tử lớn hơn 2 bên trái
27Lấy ra 2, đẩy 7 vào[7]Phần tử đầu tiên lớn hơn 7 bên trái là 7
35Đẩy 5 vào ngăn xếp[7, 5]Phần tử đầu tiên lớn hơn 5 bên trái là 7
44Đẩy 4 vào ngăn xếp[7, 5, 4]Phần tử đầu tiên lớn hơn 4 bên trái là 5
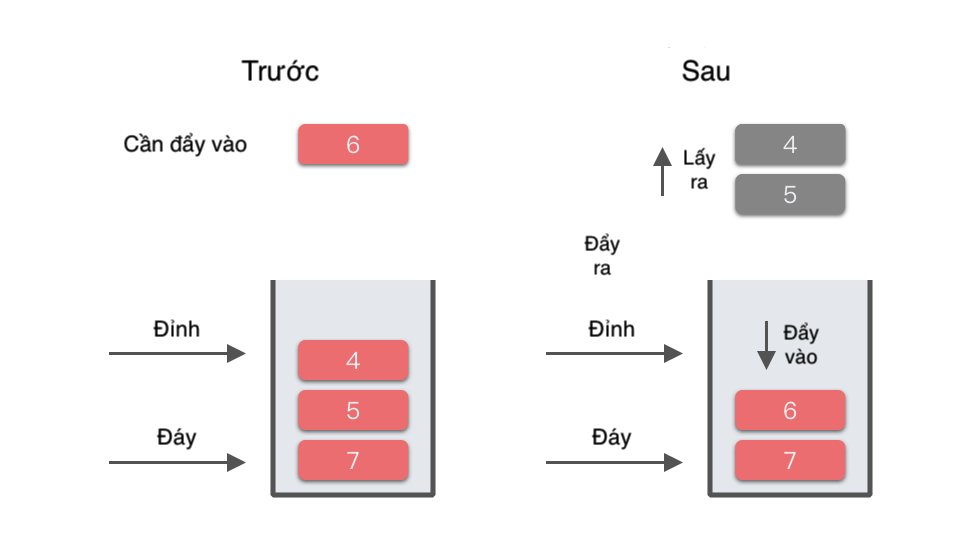
56Lấy ra 4, lấy ra 5, đẩy 6 vào[7, 6]Phần tử đầu tiên lớn hơn 6 bên trái là 7
63Đẩy 3 vào ngăn xếp[7, 6, 3]Phần tử đầu tiên lớn hơn 3 bên trái là 6
74Lấy ra 3, đẩy 4 vào[7, 6, 4]Phần tử đầu tiên lớn hơn 4 bên trái là 6
82Đẩy 2 vào ngăn xếp[7, 6, 4, 2]Phần tử đầu tiên lớn hơn 2 bên trái là 4

Cuối cùng, ngăn xếp chứa các phần tử [7, 6, 4, 2]. Vì từ đỉnh (bên phải) đến đáy (bên trái) của ngăn xếp có thứ tự 2, 4, 6, 7, thỏa mãn mối quan hệ tăng dần, nên đây là một ngăn xếp tăng dần.

Chúng ta lấy ví dụ với bước thứ 5 trong quá trình trên để minh họa:

1.2 Ngăn xếp giảm dần

Ngăn xếp giảm dần: Chỉ có các phần tử lớn hơn phần tử đỉnh của ngăn xếp mới có thể được đẩy vào ngăn xếp, nếu không, cần lấy ra các phần tử trong ngăn xếp lớn hơn hoặc bằng phần tử hiện tại trước khi đẩy phần tử hiện tại vào ngăn xếp.

Điều này đảm bảo rằng: trong ngăn xếp chỉ chứa các giá trị nhỏ hơn phần tử hiện tại và các phần tử từ đỉnh đến đáy ngăn xếp giảm dần.

Quá trình đẩy vào và lấy ra của ngăn xếp giảm dần như sau:

  • Giả sử phần tử hiện tại cần đẩy vào là x, nếu x lớn hơn phần tử đỉnh của ngăn xếp, thì đẩy x vào ngăn xếp.
  • Ngược lại, bắt đầu từ đỉnh ngăn xếp, lấy ra các phần tử trong ngăn xếp nhỏ hơn x hoặc bằng x cho đến khi gặp phần tử lớn hơn x, sau đó đẩy x vào ngăn xếp.

Dưới đây, chúng ta sẽ lấy một ví dụ với mảng [4, 3, 2, 5, 7, 4, 6, 8] để mô phỏng quá trình đẩy vào và lấy ra của "ngăn xếp giảm dần". Quá trình cụ thể như sau:

  • Mảng: [4, 3, 2, 5, 7, 4, 6, 8], thứ tự duyệt từ trái sang phải.
Bước thứ iPhần tử cần đẩy vàoThao tácKết quả (từ trái sang phải)Ý nghĩa
14Đẩy 4 vào ngăn xếp[4]Không có phần tử nhỏ hơn 4 bên trái
23Lấy ra 4, đẩy 3 vào[3]Phần tử đầu tiên nhỏ hơn 3 bên trái là 4
32Lấy ra 3, đẩy 2 vào[2]Phần tử đầu tiên nhỏ hơn 2 bên trái là 3
45Đẩy 5 vào ngăn xếp[2, 5]Phần tử đầu tiên lớn hơn 5 bên trái là 2
57Đẩy 7 vào ngăn xếp[2, 5, 7]Phần tử đầu tiên lớn hơn 7 bên trái là 5
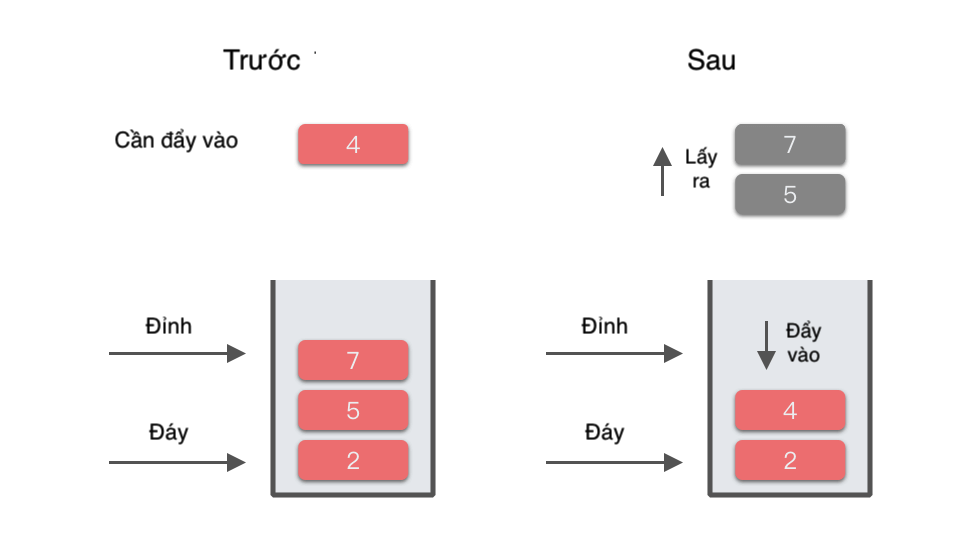
64Lấy ra 7, lấy ra 5, đẩy 4 vào[2, 4]Phần tử đầu tiên nhỏ hơn 4 bên trái là 5
76Đẩy 6 vào ngăn xếp[2, 4, 6]Phần tử đầu tiên lớn hơn 6 bên trái là 4
88Đẩy 8 vào ngăn xếp[2, 4, 6, 8]Phần tử đầu tiên lớn hơn 8 bên trái là 6

Cuối cùng, ngăn xếp chứa các phần tử [2, 4, 6, 8]. Vì từ đỉnh (bên phải) đến đáy (bên trái) của ngăn xếp có thứ tự 8, 6, 4, 2, thỏa mãn mối quan hệ giảm dần, nên đây là một ngăn xếp giảm dần.

Chúng ta lấy ví dụ với bước thứ 6 trong quá trình trên để minh họa:

20220107102446.png
20220107102446.png

2. Các trường hợp sử dụng của ngăn xếp đơn điệu

Ngăn xếp đơn điệu có thể giúp chúng ta tìm ra phần tử đầu tiên bên trái hoặc bên phải của một phần tử mà lớn hơn hoặc nhỏ hơn nó. Điều này giúp chúng ta giải quyết một số vấn đề như sau:

  • Tìm phần tử đầu tiên bên trái lớn hơn phần tử hiện tại.
  • Tìm phần tử đầu tiên bên trái nhỏ hơn phần tử hiện tại.
  • Tìm phần tử đầu tiên bên phải lớn hơn phần tử hiện tại.
  • Tìm phần tử đầu tiên bên phải nhỏ hơn phần tử hiện tại.

Dưới đây là cách giải quyết các vấn đề trên:

2.1 Tìm phần tử đầu tiên bên trái lớn hơn phần tử hiện tại

  • Duyệt các phần tử từ trái sang phải và xây dựng một ngăn xếp tăng dần (từ đỉnh đến đáy tăng dần):
    • Phần tử đầu tiên bên trái lớn hơn phần tử hiện tại chính là phần tử đầu tiên được "đẩy vào ngăn xếp tăng dần" khi duyệt qua nó.
    • Nếu ngăn xếp rỗng khi đẩy vào, có nghĩa là không có phần tử bên trái lớn hơn phần tử hiện tại.

2.2 Tìm phần tử đầu tiên bên trái nhỏ hơn phần tử hiện tại

  • Duyệt các phần tử từ trái sang phải và xây dựng một ngăn xếp giảm dần (từ đỉnh đến đáy giảm dần):
    • Phần tử đầu tiên bên trái nhỏ hơn phần tử hiện tại chính là phần tử đầu tiên được "đẩy vào ngăn xếp giảm dần" khi duyệt qua nó.
    • Nếu ngăn xếp rỗng khi đẩy vào, có nghĩa là không có phần tử bên trái nhỏ hơn phần tử hiện tại.

2.3 Tìm phần tử đầu tiên bên phải lớn hơn phần tử hiện tại

  • Duyệt các phần tử từ trái sang phải và xây dựng một ngăn xếp tăng dần (từ đỉnh đến đáy tăng dần):
    • Phần tử đầu tiên bên phải lớn hơn phần tử hiện tại chính là phần tử sẽ được "loại khỏi ngăn xếp tăng dần" khi đẩy phần tử hiện tại vào ngăn xếp.
    • Nếu phần tử không bị loại khỏi ngăn xếp, có nghĩa là không có phần tử bên phải lớn hơn phần tử hiện tại.
  • Duyệt các phần tử từ phải sang trái và xây dựng một ngăn xếp tăng dần (từ đỉnh đến đáy tăng dần):
    • Phần tử đầu tiên bên phải lớn hơn phần tử hiện tại chính là phần tử đầu tiên được "đẩy vào ngăn xếp tăng dần" khi duyệt qua nó.
    • Nếu ngăn xếp rỗng khi đẩy vào, có nghĩa là không có phần tử bên phải lớn hơn phần tử hiện tại.

2.4 Tìm phần tử đầu tiên bên phải nhỏ hơn phần tử hiện tại

  • Duyệt các phần tử từ trái sang phải và xây dựng một ngăn xếp giảm dần (từ đỉnh đến đáy giảm dần):
    • Phần tử đầu tiên bên phải nhỏ hơn phần tử hiện tại chính là phần tử sẽ được "loại khỏi ngăn xếp giảm dần" khi đẩy phần tử hiện tại vào ngăn xếp.
    • Nếu phần tử không bị loại khỏi ngăn xếp, có nghĩa là không có phần tử bên phải nhỏ hơn phần tử hiện tại.
  • Duyệt các phần tử từ phải sang trái và xây dựng một ngăn xếp giảm dần (từ đỉnh đến đáy giảm dần):
    • Phần tử đầu tiên bên phải nhỏ hơn phần tử hiện tại chính là phần tử đầu tiên được "đẩy vào ngăn xếp giảm dần" khi duyệt qua nó.
    • Nếu ngăn xếp rỗng khi đẩy vào, có nghĩa là không có phần tử bên phải nhỏ hơn phần tử hiện tại.

Trên đây là các quy tắc đơn giản để giải quyết các vấn đề sử dụng ngăn xếp đơn điệu.

Warning

Đến đây khi đọc xong có thể bạn sẽ hơi chóng mặt thì cứ từ từ khi vào các bài tập cụ thể bạn sẽ hiểu dần chúng.

3. Mẫu ngăn xếp đơn điệu

Dưới đây là mẫu để xây dựng ngăn xếp tăng dần và ngăn xếp giảm dần khi duyệt từ trái sang phải.

3.1 Mẫu ngăn xếp tăng dần

def monotoneIncreasingStack(nums):
    stack = []
    for num in nums:
        while stack and num >= stack[-1]:
            stack.pop()
        stack.append(num)

3.2 Mẫu ngăn xếp giảm dần

def monotoneDecreasingStack(nums):
    stack = []
    for num in nums:
        while stack and num <= stack[-1]:
            stack.pop()
        stack.append(num)

4. Ứng dụng của ngăn xếp đơn điệu

4.1 Phần tử lớn tiếp theo I

4.1.1 Liên kết đề bài

4.1.2 Ý nghĩa đề bài

Cho hai mảng nums1 và nums2 không có phần tử trùng lặp, trong đó nums1 là một phần con của nums2.

Yêu cầu: Với mỗi phần tử trong nums1, tìm phần tử lớn tiếp theo trong nums2.

  • Phần tử lớn hơn tiếp theo của số x trong nums1 là số lớn hơn đầu tiên đứng bên phải của x trong nums2. Nếu không có, đưa ra -1.

4.1.3 Ý tưởng giải quyết

Cách tiếp cận đầu tiên là tìm kiếm trực tiếp theo yêu cầu đề bài. Duyệt qua từng phần tử trong nums1. Đối với mỗi phần tử nums1[i], duyệt qua nums2 một lần nữa để tìm phần tử đứng bên phải đầu tiên của nums1[i] mà lớn hơn nó. Độ phức tạp thời gian của phương pháp này là O(n2)O(n^2).

Cách tiếp cận thứ hai là sử dụng ngăn xếp đơn điệu. Vì nums1 là một phần con của nums2, nên ta có thể duyệt qua nums2 một lần và xây dựng ngăn xếp đơn điệu để tìm phần tử lớn tiếp theo của mỗi phần tử trong nums2. Sau đó, lưu trữ kết quả vào một bảng băm. Sau đó, duyệt qua nums1 một lần nữa và lấy giá trị tương ứng từ bảng băm để lưu vào mảng kết quả. Phương pháp này có độ phức tạp thời gian là O(n)O(n). Cụ thể như sau:

  • Sử dụng mảng res để lưu kết quả. Sử dụng ngăn xếp stack để biểu diễn ngăn xếp đơn điệu. Sử dụng bảng băm num_map để lưu trữ phần tử lớn tiếp theo của mỗi phần tử trong nums2, với quan hệ ánh xạ là giá trị phần tử hiện tại: phần tử lớn tiếp theo của nó.
  • Duyệt qua mảng nums2, đối với phần tử hiện tại:
    • Nếu giá trị phần tử hiện tại nhỏ hơn, đẩy giá trị phần tử hiện tại vào ngăn xếp.
    • Nếu giá trị phần tử hiện tại lớn hơn, tiếp tục đẩy phần tử ra khỏi ngăn xếp cho đến khi giá trị phần tử hiện tại nhỏ hơn phần tử đầu ngăn xếp.
      • Khi đẩy phần tử ra khỏi ngăn xếp, phần tử đó là phần tử đầu tiên lớn hơn phần tử hiện tại. Lưu giá trị đó vào bảng băm num_map.
  • Sau khi duyệt qua mảng nums2 và xây dựng xong tất cả các phần tử lớn tiếp theo của mỗi phần tử, duyệt qua mảng nums1.
  • Lấy giá trị tương ứng từ bảng băm num_map và lưu vào mảng kết quả res.
  • Trả về mảng kết quả res.

4.1.4 Code

class Solution:
    def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
        res = []
        stack = []
        num_map = dict()
        for num in nums2:
            while stack and num > stack[-1]:
                num_map[stack[-1]] = num
                stack.pop()
            stack.append(num)

        for num in nums1:
            res.append(num_map.get(num, -1))
        return res

4.1.5 Ý tưởng: Phân tích độ phức tạp

  • Độ phức tạp thời gian: O(n×log2n)O(n \times log_2 n).
  • Độ phức tạp không gian: O(n)O(n).

4.2 Nhiệt độ hàng ngày

4.2.1 Liên kết đề bài

4.2.2 Ý nghĩa đề bài

Mô tả: Cho một danh sách temperatures, temperatures[i] biểu thị nhiệt độ của ngày thứ i.

Yêu cầu: Trả về một danh sách, mỗi vị trí trong danh sách đại diện cho "số ngày phải chờ ít nhất để có thể quan sát được nhiệt độ cao hơn". Nếu sau đó không còn tăng nữa, sử dụng 0 để thay thế.

Giải thích:

  • 1≤temperatures.length≤1051 \leq \text{temperatures.length} \leq 10^5.
  • 30≤temperatures[i]≤10030 \leq \text{temperatures[i]} \leq 100.

Ví dụ:

Input: temperatures = [73,74,75,71,69,72,76,73]
Output: [1,1,4,2,1,1,0,0]


Input: temperatures = [30,40,50,60]
Output: [1,1,1,0]

4.2.3 Ý tưởng giải quyết

Ý tưởng của bài toán thực chất là cho một mảng, mỗi vị trí có giá trị nguyên. Đối với mỗi vị trí, tìm vị trí đầu tiên bên phải của nó mà có giá trị lớn hơn. Tính khoảng cách giữa "phần tử hiện tại" và "phần tử lớn tiếp theo bên phải" và lưu tất cả các khoảng cách đó vào một mảng và trả về kết quả.

Cách tiếp cận đơn giản nhất là tìm kiếm tuần tự cho mỗi nhiệt độ, tìm vị trí đầu tiên bên phải mà có nhiệt độ cao hơn hiện tại.

Cách tiếp cận tốt hơn là sử dụng "ngăn xếp đơn điệu". Ngăn xếp sẽ lưu trữ các chỉ số của các phần tử.

Ý tưởng 1: Ngăn xếp đơn điệu
  1. Đầu tiên, gán tất cả các phần tử trong mảng kết quả ans bằng 0. Sau đó duyệt qua từng vị trí trong mảng.
  2. Nếu ngăn xếp rỗng, đưa chỉ số hiện tại vào ngăn xếp.
  3. Nếu ngăn xếp không rỗng và số hiện tại lớn hơn số tại đỉnh ngăn xếp, lấy phần tử đỉnh ngăn xếp ra khỏi ngăn xếp và tính khoảng cách giữa chỉ số hiện tại và chỉ số đỉnh ngăn xếp.
  4. Lúc này, số hiện tại là số đầu tiên lớn hơn số hiện tại. Lưu khoảng cách đó vào mảng kết quả ans.
  5. Lặp lại bước 3 và 4 cho đến khi số hiện tại nhỏ hơn hoặc bằng số đỉnh ngăn xếp.
  6. Cuối cùng, trả về mảng kết quả ans.
Ý tưởng 1: Đoạn mã
class Solution:
    def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
        n = len(temperatures)
        stack = []
        ans = [0] * n
        for i in range(n):
            while stack and temperatures[i] > temperatures[stack[-1]]:
                index = stack.pop()
                ans[index] = (i - index)
            stack.append(i)
        return ans
Ý tưởng 1: Phân tích độ phức tạp
  • Độ phức tạp thời gian: O(n)O(n).
  • Độ phức tạp không gian: O(n)O(n).
Made with ❤️ by Hung Nguyen
Copyright © 2016-2024 Hung Nguyen