Heap

1. Định nghĩa Heap

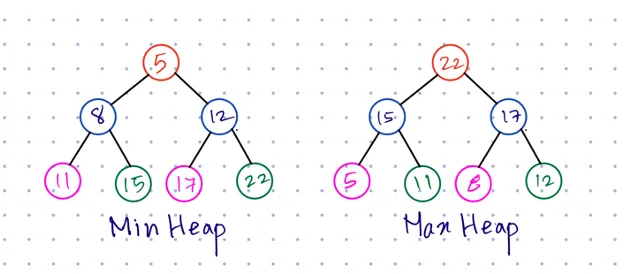
Heap: Một loại cây nhị phân hoàn chỉnh thỏa mãn một trong hai điều kiện sau:
Max Heap: Giá trị của mọi nút lớn hơn hoặc bằng giá trị của các nút con của nó.
Min Heap: Giá trị của mọi nút nhỏ hơn hoặc bằng giá trị của các nút con của nó.

Cấu trúc logic của Heap là một cây nhị phân hoàn chỉnh. Và chúng ta đã học trong phần [[Binary Tree Basic]] rằng, đối với cây nhị phân hoàn chỉnh (đặc biệt là cây nhị phân đầy đủ), việc sử dụng cấu trúc lưu trữ tuần tự (mảng) để biểu diễn cây nhị phân hoàn chỉnh có thể tận dụng tối đa không gian lưu trữ.

Khi sử dụng cấu trúc lưu trữ tuần tự (mảng) để biểu diễn Heap, quan hệ giữa chỉ mục của các phần tử trong Heap và chỉ mục của mảng như sau:

Nếu chỉ mục của một nút cây nhị phân (không phải lá) là $i$ , thì chỉ mục của nút con trái là $2 \times i + 1$ , chỉ mục của nút con phải là $2 \times i + 2$ .
Nếu chỉ mục của một nút cây nhị phân (không phải gốc) là $i$ , thì chỉ mục của nút gốc là $\lfloor \frac{i - 1}{2} \rfloor$ (làm tròn xuống).

class MaxHeap:
    def __init__(self):
        self.max_heap = []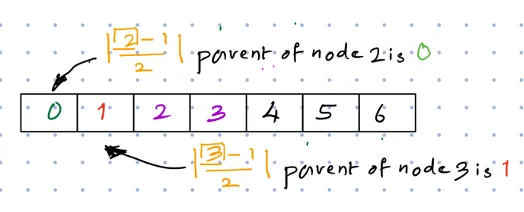

3. Truy cập phần tử đỉnh Heap

Truy cập phần tử đỉnh Heap: Đề cập đến việc lấy phần tử đầu tiên trong Heap.

Trong Heap, phần tử đỉnh nằm ở nút gốc, khi chúng ta sử dụng cấu trúc lưu trữ tuần tự (mảng) để biểu diễn Heap, phần tử đỉnh là phần tử đầu tiên của mảng.

class MaxHeap:
    ......
    def peek(self) -> int:
        # Max Heap trống
        if not self.max_heap:
            return None
        # Trả về phần tử đỉnh Heap
        return self.max_heap[0]

Việc truy cập phần tử đỉnh Heap không phụ thuộc vào số lượng phần tử trong mảng, do đó độ phức tạp thời gian là $O(1)$ .

4. Chèn phần tử vào Heap

Chèn phần tử vào Heap: Đề cập đến việc thêm một phần tử mới vào Heap, điều chỉnh cấu trúc Heap để giữ nguyên tính chất của Heap.

Các bước để chèn phần tử vào Heap như sau:

Thêm phần tử mới vào cuối Heap, giữ nguyên cấu trúc cây nhị phân hoàn chỉnh.
Bắt đầu từ nút chứa phần tử mới chèn, so sánh nút này với nút cha của nó.
1. Nếu giá trị của nút mới lớn hơn giá trị của nút cha của nó, hoán đổi chúng để giữ tính chất của Max Heap.
2. Nếu giá trị của nút mới nhỏ hơn hoặc bằng giá trị của nút cha của nó, điều này có nghĩa là Max Heap đã đáp ứng yêu cầu, kết thúc quá trình.
Lặp lại các bước so sánh và hoán đổi trên, cho đến khi nút mới không còn lớn hơn nút cha của nó hoặc đạt đến nút gốc của Heap.

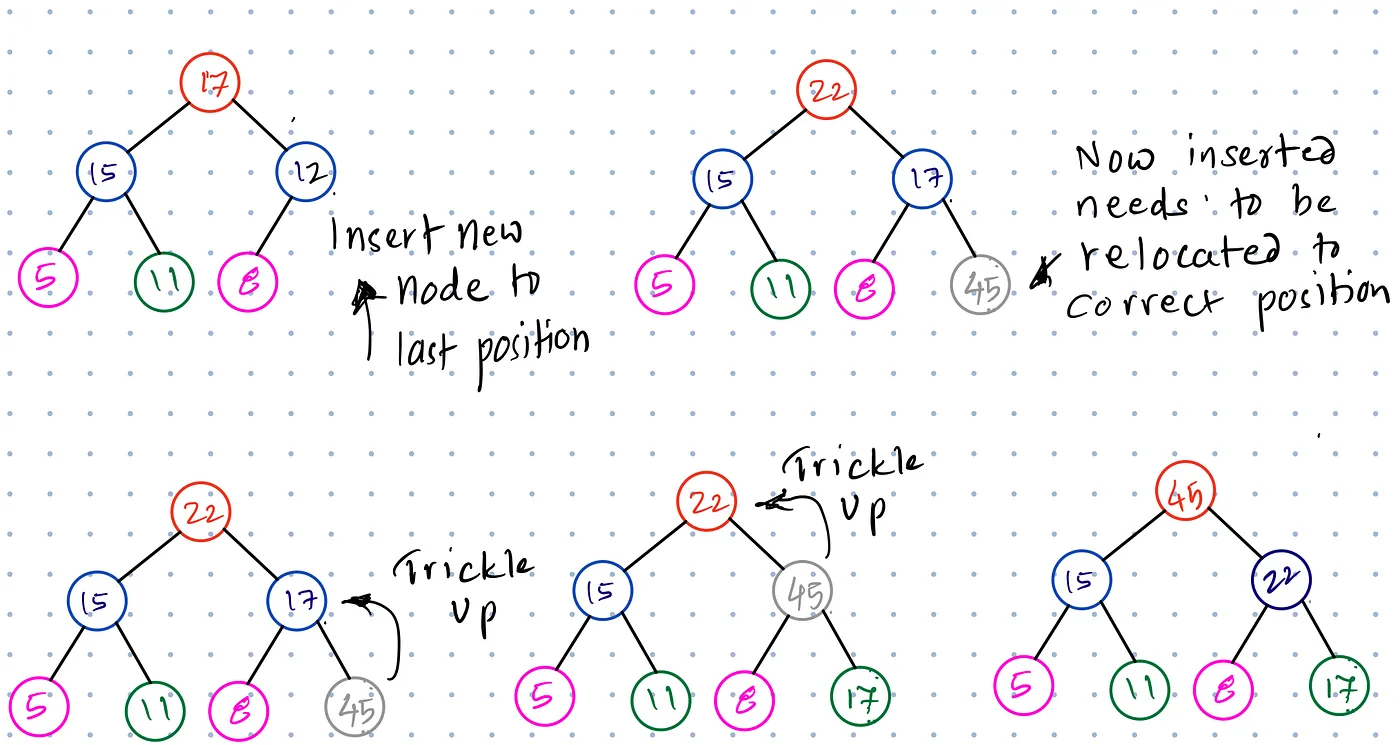
Quá trình này được gọi là "điều chỉnh lên" (Shift Up). Vì phần tử mới chèn sẽ di chuyển lên từng bước cho đến khi tìm được vị trí phù hợp, giữ tính chất được sắp xếp của Heap.

class MaxHeap:
    ......
    def push(self, val: int):
        # Thêm phần tử mới vào cuối Heap
        self.max_heap.append(val)
        
        size = len(self.max_heap)
        # Bắt đầu từ nút chứa phần tử mới chèn, thực hiện điều chỉnh lên
        self.__shift_up(size - 1)
        
    def __shift_up(self, i: int):
        while (i - 1) // 2 >= 0 and self.max_heap[i] > self.max_heap[(i - 1) // 2]:
            self.max_heap[i], self.max_heap[(i - 1) // 2] = self.max_heap[(i - 1) // 2], self.max_heap[i]
            i = (i - 1) // 2

Trong trường hợp xấu nhất, độ phức tạp thời gian của "chèn phần tử vào Heap" là $O(\log n)$ , trong đó $n$ là số lượng phần tử trong Heap, điều này bởi vì chiều cao của Heap là $\log n$ .

5. Xóa phần tử đỉnh Heap

Xóa phần tử đỉnh Heap: Đề cập đến việc loại bỏ phần tử đầu tiên trong Heap và điều chỉnh lại cấu trúc Heap để giữ nguyên tính chất của Heap.

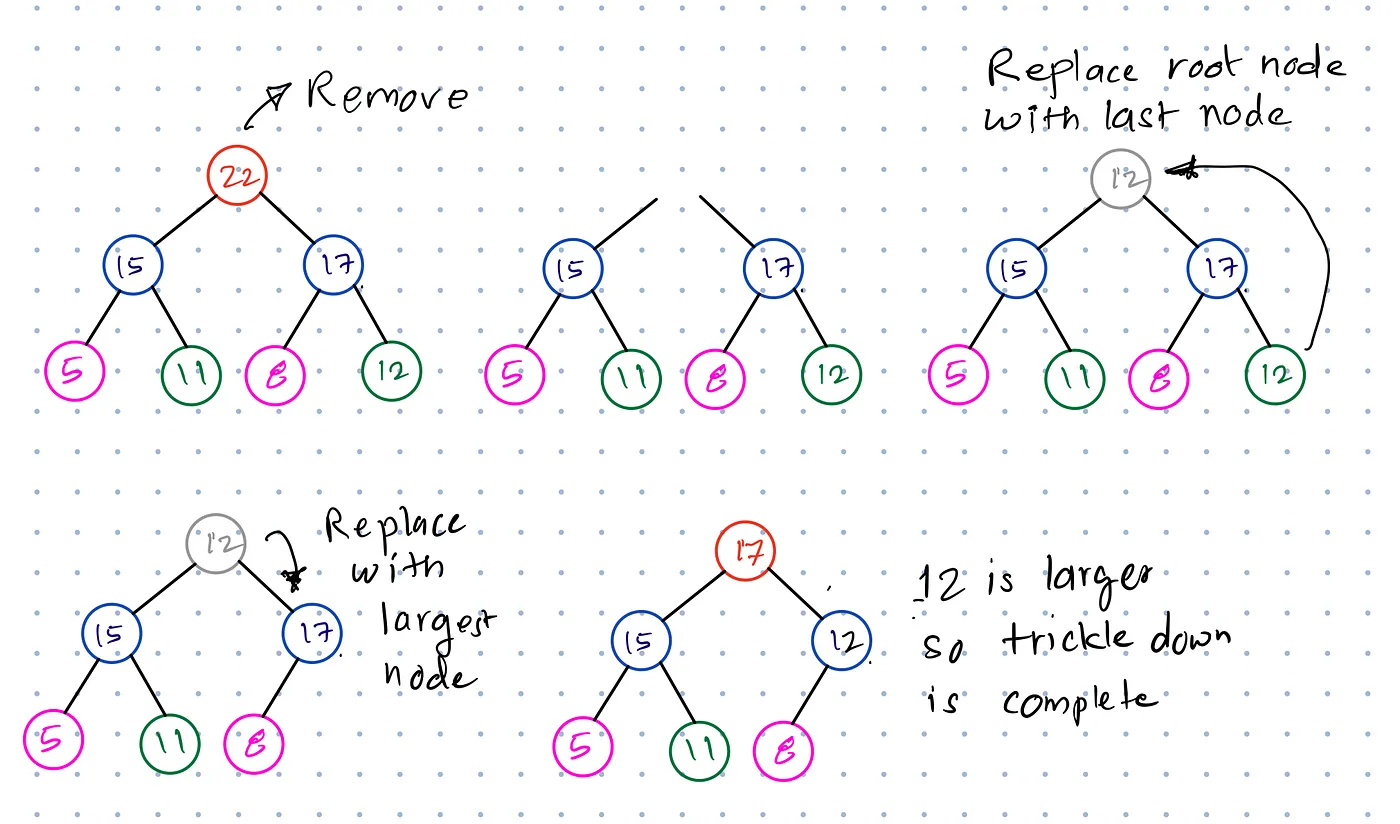
Các bước để xóa phần tử đỉnh Heap như sau:

Hoán đổi phần tử đỉnh (tức là nút gốc) với phần tử cuối cùng của Heap.
Loại bỏ phần tử cuối cùng của Heap (phần tử đỉnh cũ), tức là loại bỏ nó khỏi Heap.
Bắt đầu từ phần tử đỉnh mới, so sánh nó với nút con lớn hơn của nó.
1. Nếu giá trị của nút hiện tại nhỏ hơn giá trị của nút con lớn hơn, hoán đổi chúng. Bước này được thực hiện để "đẩy" phần tử đỉnh mới xuống vị trí thích hợp, giữ tính chất của Max Heap.
2. Nếu giá trị của nút hiện tại lớn hơn hoặc bằng giá trị của nút con lớn hơn, điều này có nghĩa là Max Heap đã đáp ứng yêu cầu, kết thúc quá trình.
Lặp lại các bước so sánh và hoán đổi trên, cho đến khi phần tử đỉnh mới không còn nhỏ hơn nút con của nó hoặc đạt đến đáy của Heap.

Quá trình này được gọi là "điều chỉnh xuống" (Shift Down). Vì phần tử đỉnh mới sẽ di chuyển xuống từng bước cho đến khi tìm được vị trí phù hợp, giữ tính chất được sắp xếp của Heap.

class MaxHeap:
    ......        
    def pop(self) -> int:
        # Heap rỗng
        if not self.max_heap:
            raise IndexError("Heap rỗng")
        
        size = len(self.max_heap)
        self.max_heap[0], self.max_heap[size - 1] = self.max_heap[size - 1], self.max_heap[0]
        # Xóa phần tử đỉnh Heap
        val = self.max_heap.pop()
        # Giảm số lượng nút đi 1
        size -= 1 
        
        # Điều chỉnh xuống
        self.__shift_down(0, size)
        
        # Trả về phần tử đỉnh Heap
        return val

    
    def __shift_down(self, i: int, n: int):
        while 2 * i + 1 < n:
            # Chỉ mục của nút con trái và nút con phải
            left, right = 2 * i + 1, 2 * i + 2
            
            # Tìm chỉ mục của nút con lớn hơn trong nút con trái và nút con phải
            if 2 * i + 2 >= n:
                # Chỉ mục của nút con phải vượt quá phạm vi (chỉ có nút con trái)
                larger = left
            else:
                # Cả nút con trái và nút con phải đều tồn tại
                if self.max_heap[left] >= self.max_heap[right]:
                    larger = left
                else:
                    larger = right
            
            # So sánh giá trị của nút hiện tại với nút con lớn hơn
            if self.max_heap[i] < self.max_heap[larger]:
                # Nếu giá trị của nút hiện tại nhỏ hơn giá trị của nút con lớn hơn, hoán đổi chúng
                self.max_heap[i], self.max_heap[larger] = self.max_heap[larger], self.max_heap[i]
                i = larger
            else:
                # Nếu giá trị của nút hiện tại lớn hơn hoặc bằng giá trị của nút con lớn hơn, kết thúc quá trình
                break

Thời gian phức tạp của "xóa phần tử đỉnh Heap" thường là $O(\log n)$ , trong đó $n$ là số lượng phần tử trong Heap, vì chiều cao của Heap là $\log n$ .

6. Ứng dụng phổ biến của Heap

Hàng đợi ưu tiên: Heap thường được sử dụng làm cấu trúc dữ liệu chính để triển khai hàng đợi ưu tiên, với thời gian thêm và xóa phần tử là $O(\log n)$ và thời gian xây dựng hàng đợi là $O(n)$ , các thao tác này đều rất hiệu quả.
[[Heap Sort]]: Cho một tập hợp dữ liệu, chúng ta có thể xây dựng một heap từ nó và sau đó liên tục thực hiện các thao tác xóa phần tử để thu được dữ liệu đã được sắp xếp. Tuy nhiên, thường chúng ta sẽ sử dụng một cách tiếp cận tinh vi hơn để triển khai thuật toán sắp xếp heap, chi tiết xem trong phần sắp xếp heap sau.
Bài toán Top-K: Đây là một bài toán thuật toán kinh điển, cũng là một ứng dụng điển hình, ví dụ như chọn 10 tin tức nổi bật nhất làm chủ đề hot trên mạng xã hội, chọn 10 sản phẩm bán chạy nhất, v.v.