Hash Table

1. Giới thiệu về bảng băm

Bảng băm (Hash Table): còn được gọi là bảng phân tán. Đây là một cấu trúc dữ liệu cho phép truy cập trực tiếp vào dữ liệu dựa trên giá trị khóa (Key Value).

Bảng băm sử dụng hàm băm (Hash function) để tính toán giá trị tương ứng với khóa (key), và lưu trữ giá trị tương ứng vào một vị trí trong bảng để tăng tốc độ tìm kiếm. Hàm băm này còn được gọi là "hàm băm (hàm phân tán)", và mảng lưu trữ các giá trị được gọi là "bảng băm (bảng phân tán)".

Ý tưởng chính của bảng băm là sử dụng hàm băm để ánh xạ khóa (key) vào một vùng nhớ trong bảng. Có thể chia thuật toán thành hai phần:

• Chèn một giá trị vào bảng băm: Hàm băm quyết định giá trị tương ứng với khóa nên được lưu trữ trong vùng nhớ nào trong bảng, sau đó giá trị đó được lưu trữ vào vùng nhớ đó.
• Tìm kiếm một giá trị trong bảng băm: Sử dụng cùng hàm băm để tìm vùng nhớ tương ứng trong bảng, sau đó tìm kiếm giá trị tương ứng với khóa trong vùng nhớ đó.

Hình minh họa nguyên lý của bảng băm như sau:

20220114120000.png

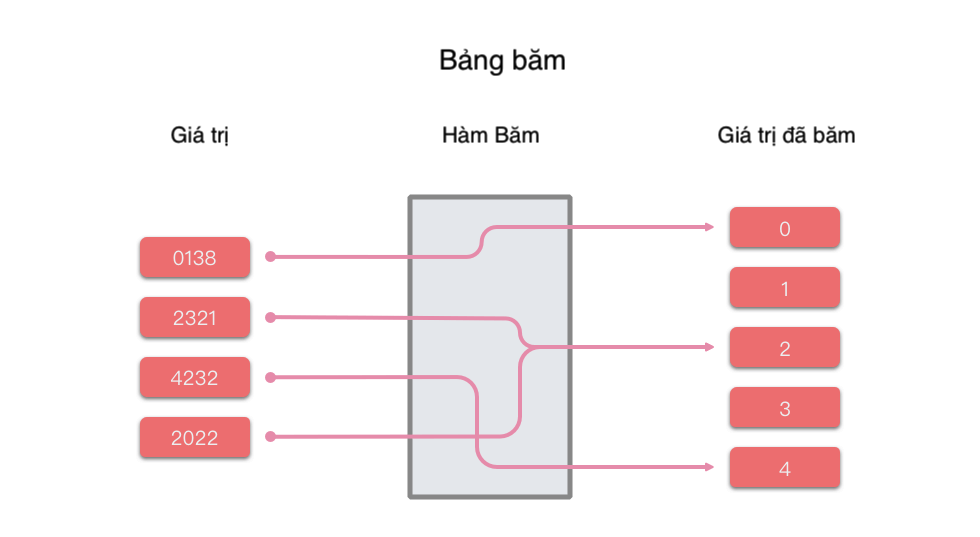
Trong ví dụ trên, chúng ta sử dụng hàm value = Hash(key) = key // 1000 làm hàm băm. Dưới đây là mô tả quá trình chèn và tìm kiếm trong bảng băm.

• Chèn một giá trị vào bảng băm: Sử dụng hàm băm để ánh xạ khóa và lưu trữ giá trị tương ứng vào vùng nhớ đó.
  • Ví dụ: Khóa 0138 thông qua hàm băm Hash(key) = 0138 // 100 = 0, ta biết rằng giá trị 0138 sẽ được lưu trữ trong vùng nhớ của khối 0.
• Tìm kiếm một giá trị trong bảng băm: Sử dụng hàm băm để ánh xạ khóa và tìm kiếm giá trị tương ứng trong vùng nhớ đó.
  • Ví dụ: Tìm kiếm 2321, thông qua hàm băm, ta biết rằng 2321 sẽ nằm trong vùng nhớ tương ứng với khối 2. Sau đó, chúng ta tiếp tục tìm kiếm trong vùng nhớ của khối 2 và thành công tìm thấy giá trị 2321.
  • Ví dụ: Tìm kiếm 3214, thông qua hàm băm, ta biết rằng 3214 sẽ nằm trong vùng nhớ tương ứng với khối 3. Sau đó, chúng ta tiếp tục tìm kiếm trong vùng nhớ của khối 3 nhưng không tìm thấy giá trị, điều này cho thấy 3214 không có trong bảng băm.

2. Hàm băm

Hàm băm (Hash Function): Là hàm ánh xạ giá trị khóa của các phần tử trong bảng băm thành vị trí lưu trữ của phần tử đó.

Hàm băm là một phần quan trọng nhất trong bảng băm. Thông thường, hàm băm phải đáp ứng các điều kiện sau:

• Hàm băm nên dễ tính toán và giá trị chỉ mục tính toán ra phân bố đều.
• Giá trị băm tính toán được là một giá trị đầu ra có độ dài cố định.
• Nếu Hash(key1) không bằng Hash(key2), thì key1 và key2 chắc chắn không bằng nhau.
• Nếu Hash(key1) bằng Hash(key2), thì key1 và key2 có thể bằng nhau hoặc không bằng nhau (xảy ra va chạm băm).

Trong ứng dụng thực tế của bảng băm, loại khóa không chỉ là số, mà còn có thể là chuỗi, số thực, số nguyên lớn, thậm chí là sự kết hợp của một số loại. Thông thường, chúng ta sẽ chuyển đổi các loại khóa thành loại số nguyên trước, sau đó sử dụng hàm băm để ánh xạ chúng vào bảng băm.

Đối với loại khóa là số nguyên, các phương pháp hàm băm thường được sử dụng bao gồm: phương pháp địa chỉ trực tiếp, phương pháp chia lấy dư, phương pháp bình phương lấy giữa, phương pháp chuyển đổi cơ số, phương pháp phân tích số, phương pháp gập, phương pháp số ngẫu nhiên, phương pháp nhân, phương pháp tích vô hướng, v.v. Dưới đây, chúng ta sẽ giới thiệu một số phương pháp hàm băm phổ biến.

2.1 Phương pháp địa chỉ trực tiếp

• Phương pháp địa chỉ trực tiếp: Lấy chính giá trị khóa hoặc một hàm tuyến tính của khóa làm địa chỉ băm. Tức là: Hash(key) = key hoặc Hash(key) = a * key + b, trong đó a và b là các hằng số.

Phương pháp này tính toán đơn giản nhất và không gây ra va chạm. Phù hợp cho trường hợp khóa phân bố liên tục cơ bản, nếu khóa không phân bố liên tục và có nhiều khoảng trống, sẽ dẫn đến lãng phí không gian lưu trữ.

Ví dụ, giả sử chúng ta có một bảng thống kê dân số từ 1 đến 100 tuổi. Trong đó, tuổi là khóa, hàm băm lấy chính giá trị khóa, như bảng dưới đây.

Tuổi	1	2	3	…	25	26	27	…	100
Dân số	3000	2000	5000	…	1050	…	…	…	…

Ví dụ, nếu chúng ta muốn tìm số người 25 tuổi, chỉ cần truy vấn mục 25 trong bảng.

2.2 Phương pháp chia lấy dư

• Phương pháp chia lấy dư: Giả sử chiều dài bảng băm là m, chọn một số nguyên tố p không lớn hơn m, sử dụng phép chia lấy dư để chuyển đổi khóa thành địa chỉ băm. Tức là: Hash(key) = key % p, trong đó p là số nguyên tố không lớn hơn m.

Đây cũng là một phương pháp đơn giản và phổ biến của hàm băm. Điểm quan trọng là chọn giá trị p. Theo kinh nghiệm, thông thường chọn p là số nguyên tố hoặc m, điều này giúp giảm thiểu va chạm.

Ví dụ, chúng ta cần lưu trữ 7 số [432, 5, 128, 193, 92, 111, 88] trong 11 khối (mảng có độ dài 11) bằng phương pháp chia lấy dư, các số này sẽ được phân bố như sau:

Chỉ mục	00	01	02	03	04	05	06	07	08	09	10
Dữ liệu	88	111		432	92	5	193		128

2.3 Phương pháp bình phương lấy giữa

• Phương pháp bình phương lấy giữa: Đầu tiên, tăng cường sự khác biệt giữa các số gần nhau bằng cách lấy bình phương của khóa, sau đó lấy giữa một số chữ số của giá trị bình phương khóa làm địa chỉ băm.
  • Ví dụ: Hash(key) = (key * key) // 100 % 1000, tính bình phương trước, loại bỏ 2 chữ số cuối cùng, sau đó lấy 3 chữ số giữa làm địa chỉ băm.

Phương pháp này vì giá trị giữa một số chữ số của giá trị bình phương và từng chữ số của khóa gốc có liên quan, nên địa chỉ băm được tạo ra cũng khá đều, giúp giảm thiểu va chạm.

2.4 Phương pháp chuyển đổi cơ số

• Phương pháp chuyển đổi cơ số: Xem khóa như là một số hệ cơ số khác, sau đó chuyển đổi nó thành số hệ cơ số ban đầu, sau đó chọn một số chữ số trong số đó làm địa chỉ băm.
  • Ví dụ, xem khóa như là số hệ 13, sau đó chuyển đổi nó thành số hệ 10, sau đó lấy số đó làm địa chỉ băm.

Ví dụ với số 343246, cách tính địa chỉ băm như sau:

$343246_{13} = 3 \times 13^5 + 4 \times 13^4 + 3 \times 13^3 + 2 \times 13^2 + 4 \times 13^1 + 6 \times 13^0 = 1235110_{10}$

3. Xung đột băm

Xung đột băm (Hash Collision): Khi các khóa khác nhau thông qua cùng một hàm băm có thể có cùng một địa chỉ băm, tức là key1 ≠ key2, nhưng Hash(key1) = Hash(key2), hiện tượng này được gọi là xung đột băm.

Trong trạng thái lý tưởng, hàm băm của chúng ta là một ánh xạ một một hoàn hảo, có nghĩa là một khóa (key) tương ứng với một giá trị (value), không cần xử lý xung đột. Tuy nhiên, trong hầu hết các trường hợp, các khóa khác nhau key có thể tương ứng với cùng một giá trị value, điều này gọi là xung đột băm.

Không có cách nào để tránh hoàn toàn xung đột băm, ngay cả khi thiết kế hàm băm tốt nhất. Do đó, chúng ta cần sử dụng các phương pháp nhất định để giải quyết vấn đề xung đột băm. Các phương pháp phổ biến để giải quyết xung đột bao gồm hai loại chính: phương pháp địa chỉ mở (Open Addressing) và phương pháp nối (Chaining).

3.1 Phương pháp địa chỉ mở

Phương pháp địa chỉ mở (Open Addressing): Đề cập đến việc mở địa chỉ trống trong bảng băm để xử lý xung đột. Khi bảng băm chưa đầy, khi xảy ra xung đột, chúng ta cần thử một đơn vị khác, cho đến khi tìm thấy một đơn vị trống.

Khi xảy ra xung đột, phương pháp địa chỉ mở sẽ tính toán địa chỉ băm kế tiếp theo theo công thức sau: H(i) = (Hash(key) + F(i)) % m, i = 1, 2, 3, …, n (n ≤ m - 1).

• H(i) là chuỗi địa chỉ được tạo ra trong quá trình xử lý xung đột. Nghĩa là trong lần xung đột thứ nhất (i = 1), chúng ta tính toán được một địa chỉ mới H(1) sau khi xử lý xung đột, nếu xảy ra xung đột tại H(1) (khi i = 2), chúng ta tính toán được một địa chỉ mới khác H(2) … và tiếp tục như vậy cho đến khi tìm được H(n) mà không xảy ra xung đột nữa.
• Hash(key) là hàm băm, m là độ dài của bảng băm, việc lấy phần dư của độ dài bảng băm nhằm đảm bảo rằng địa chỉ tiếp theo luôn nằm trong bảng băm.
• F(i) là phương pháp giải quyết xung đột, có thể chọn từ các phương pháp sau:
  • Phương pháp tìm kiếm tuyến tính: $F(i) = 1, 2, 3, …, m - 1$.
  • Phương pháp tìm kiếm bình phương: $F(i) = 1^2, -1^2, 2^2, -2^2, …, \pm n^2(n \le m / 2)$.
  • Chuỗi số giả ngẫu nhiên: $F(i) = \text{Chuỗi số giả ngẫu nhiên}$.

Hãy xem một ví dụ để hiểu cách sử dụng ba phương pháp giải quyết xung đột trên và tìm được địa chỉ mới H(i). Ví dụ, trong bảng băm có độ dài 11 đã được điền các bản ghi với các khóa tương ứng là 28, 49, 18 (hàm băm là Hash(key) = key % 11). Bây giờ chúng ta muốn chèn một bản ghi mới với khóa 38. Dựa trên hàm băm, địa chỉ băm tương ứng là 5, và xảy ra xung đột. Tiếp theo, chúng ta sẽ sử dụng ba phương pháp giải quyết xung đột này để xử lý xung đột.

• Sử dụng phương pháp tìm kiếm tuyến tính: Tìm được địa chỉ tiếp theo H(1) = (5 + 1) % 11 = 6, vẫn xảy ra xung đột; tiếp tục tìm được H(2) = (5 + 2) % 11 = 7, vẫn xảy ra xung đột; tiếp tục tìm được H(3) = (5 + 3) % 11 = 8, địa chỉ 8 trống, quá trình xử lý xung đột kết thúc, ghi chú được chèn vào vị trí 8 của bảng băm.
• Sử dụng phương pháp tìm kiếm bình phương: Tìm được địa chỉ tiếp theo H(1) = (5 + 1*1) % 11 = 6, vẫn xảy ra xung đột; tiếp tục tìm được H(2) = (5 - 1*1) % 11 = 4, địa chỉ 4 trống, quá trình xử lý xung đột kết thúc, ghi chú được chèn vào vị trí 4 của bảng băm.
• Sử dụng chuỗi số giả ngẫu nhiên: Giả sử số giả ngẫu nhiên là 9, sau đó tìm được địa chỉ tiếp theo H(1) = (9 + 5) % 11 = 3, địa chỉ 3 trống, quá trình xử lý xung đột kết thúc, ghi chú được chèn vào vị trí 3 của bảng băm.

Kết quả của việc sử dụng ba phương pháp giải quyết xung đột này được thể hiện trong hình sau:

20220115162728.png

3.2 Phương pháp nối

Phương pháp nối (Chaining): Lưu trữ các phần tử (hoặc bản ghi) có cùng địa chỉ băm trong cùng một danh sách liên kết.

Phương pháp nối là một phương pháp giải quyết xung đột thông dụng hơn. So với phương pháp địa chỉ mở, phương pháp nối đơn giản hơn.

Chúng ta giả sử địa chỉ băm được tạo bởi hàm băm là [0, m - 1], độ dài của bảng băm là m. Ta có thể định nghĩa bảng băm là một mảng con trỏ danh sách liên kết T với m phần tử.

• Khi chèn khóa, chúng ta chỉ cần tính toán địa chỉ băm tương ứng bằng hàm băm Hash(key), sau đó chèn nó dưới dạng một nút liên kết vào danh sách liên kết với đầu danh sách là T[i]. Vị trí chèn có thể ở đầu danh sách hoặc cuối danh sách, hoặc ở giữa. Nếu chèn ở đầu danh sách, thời gian chèn là $O(1)$.
• Khi tìm kiếm khóa, chúng ta chỉ cần tính toán địa chỉ băm tương ứng bằng hàm băm Hash(key), sau đó quét toàn bộ danh sách liên kết tại vị trí tương ứng T[i], so sánh giá trị khóa của từng nút liên kết với khóa tìm kiếm. Thời gian tìm kiếm là $O(k)$, với k là độ dài của danh sách liên kết. Đối với hàm băm có phân bố đồng đều của địa chỉ băm, lý thuyết là k = n // m, trong đó n là số lượng khóa và m là độ dài của bảng băm.

Hãy xem một ví dụ để hiểu cách sử dụng phương pháp nối để giải quyết xung đột. Giả sử chúng ta có một tập hợp các khóa cần lưu trữ keys = [88, 60, 65, 69, 90, 39, 07, 06, 14, 44, 52, 70, 21, 45, 19, 32]. Giả sử hàm băm là Hash(key) = key % 13, độ dài của bảng băm m = 13, và phạm vi địa chỉ băm là [0, m - 1]. Sử dụng phương pháp nối, chúng ta xử lý xung đột và chèn các khóa theo thứ tự vào bảng băm (được biểu diễn dưới dạng chèn vào cuối danh sách liên kết), kết quả cuối cùng là bảng băm như hình dưới đây.

20220115182535.png

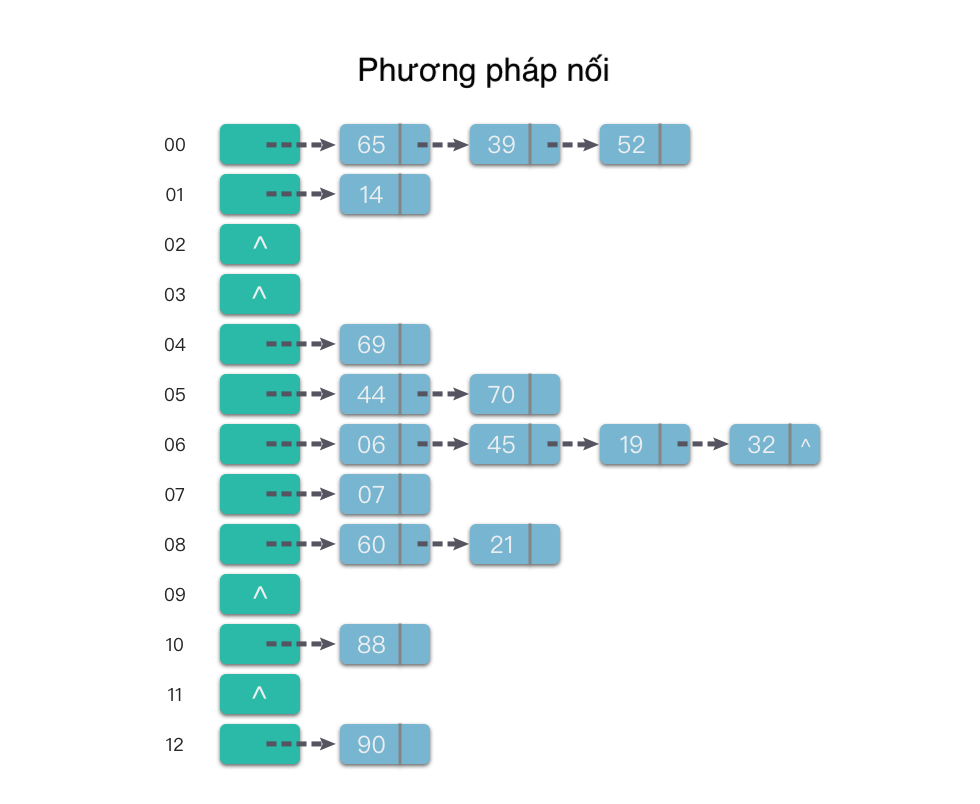
So với phương pháp địa chỉ mở, phương pháp nối tiêu thụ một số không gian lưu trữ hơn (chủ yếu là không gian lưu trữ cho các nút liên kết). Tuy nhiên, nó có thể giảm thiểu độ dài trung bình của quá trình tìm kiếm khi thực hiện việc chèn và tìm kiếm các khóa có cùng địa chỉ băm. Điều này bởi vì trong phương pháp nối, các khóa cần so sánh trong quá trình tìm kiếm là các phần tử có cùng địa chỉ băm, trong khi trong phương pháp địa chỉ mở, các khóa cần so sánh không chỉ bao gồm các phần tử có cùng địa chỉ băm mà còn bao gồm các phần tử có địa chỉ băm khác nhau.

4. Tổng kết bảng băm

Bài viết này đã giải thích một số kiến thức cơ bản và lý thuyết về bảng băm. Bao gồm định nghĩa của bảng băm, hàm băm, xung đột băm và các phương pháp giải quyết xung đột băm.

• Bảng băm (Hash Table): Sử dụng khóa key và một hàm ánh xạ Hash(key) để tính toán giá trị value tương ứng, giúp tăng tốc độ tìm kiếm trong quá trình truy cập dữ liệu.
• Hàm băm (Hash Function): Là hàm ánh xạ giá trị khóa của các phần tử trong bảng băm thành vị trí lưu trữ của phần tử đó.
• Xung đột băm (Hash Collision): Khi các khóa khác nhau thông qua cùng một hàm băm có thể có cùng một địa chỉ băm.

Hai vấn đề cốt lõi của bảng băm là: "xây dựng hàm băm" và "giải quyết xung đột băm".

• Các phương pháp phổ biến để xây dựng hàm băm bao gồm: phương pháp địa chỉ trực tiếp, phương pháp chia lấy dư, phương pháp bình phương lấy giữa, phương pháp chuyển đổi cơ số, phương pháp phân tích số, phương pháp gập, phương pháp số ngẫu nhiên, phương pháp nhân, phương pháp tích vô hướng, v.v.
• Các phương pháp giải quyết xung đột phổ biến bao gồm hai loại: phương pháp địa chỉ mở và phương pháp nối.