Sliding Window

1. Giới thiệu thuật toán cửa sổ trượt

Trong mạng máy tính, giao thức cửa sổ trượt (Sliding Window Protocol) là một biện pháp điều khiển luồng trong tầng transport, bên nhận thông báo cho bên gửi về kích thước cửa sổ của mình để kiểm soát tốc độ gửi của bên gửi, nhằm tránh bị ngập lụt bởi tốc độ gửi quá nhanh của bên gửi. Thuật toán cửa sổ trượt mà chúng ta sẽ trình bày cũng sử dụng các tính chất tương tự.

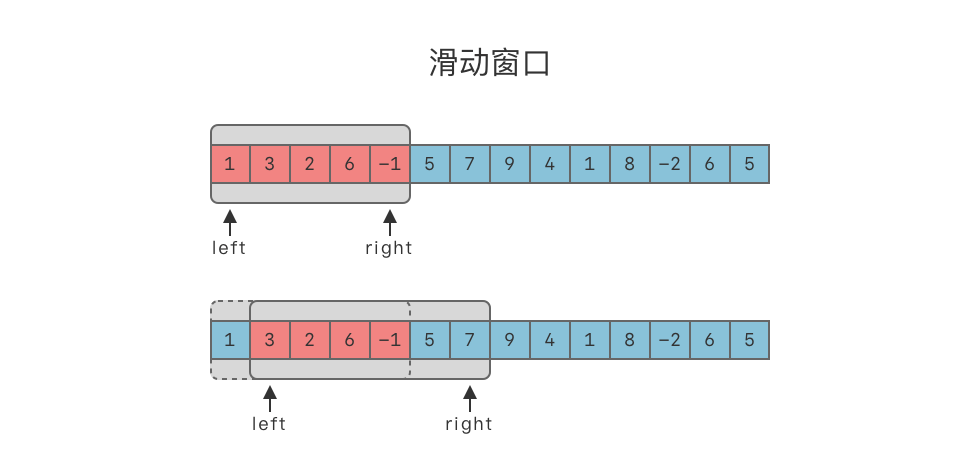
Thuật toán cửa sổ trượt (Sliding Window): Duy trì một cửa sổ có độ dài cố định hoặc không cố định trên một mảng / chuỗi đã cho. Có thể thực hiện các hoạt động trượt cửa sổ, co giãn cửa sổ và duy trì giải pháp tối ưu.

Hoạt động trượt: Cửa sổ có thể di chuyển theo một hướng nhất định. Thường thì di chuyển sang phải là phổ biến nhất.
Hoạt động co giãn: Đối với cửa sổ không cố định, có thể thu nhỏ độ dài cửa sổ từ phía trái hoặc tăng độ dài cửa sổ từ phía phải.

Thuật toán cửa sổ trượt tận dụng kỹ thuật con trỏ nhanh / chậm, chúng ta có thể coi cửa sổ trượt là một phần của khoảng giữa hai con trỏ nhanh / chậm, hoặc có thể coi cửa sổ trượt là một dạng đặc biệt của con trỏ nhanh / chậm.

2. Phạm vi áp dụng của cửa sổ trượt

Thuật toán cửa sổ trượt thường được sử dụng để giải quyết các vấn đề liên quan đến tìm kiếm các đoạn liên tiếp thỏa mãn một số điều kiện (độ dài, v.v.) cụ thể. Thuật toán này có thể chuyển đổi một phần của vòng lặp lồng nhau trong một vòng lặp đơn, do đó nó giúp giảm độ phức tạp thời gian.

Dựa trên độ dài cửa sổ cố định, chúng ta có thể chia các bài toán cửa sổ trượt thành hai loại sau:

Cửa sổ độ dài cố định: Kích thước cửa sổ là cố định.
Cửa sổ độ dài không cố định: Kích thước cửa sổ không cố định.
- Tìm cửa sổ lớn nhất thỏa mãn điều kiện.
- Tìm cửa sổ nhỏ nhất thỏa mãn điều kiện.

Dưới đây sẽ trình bày cụ thể về hai loại bài toán này.

3. Cửa sổ trượt độ dài cố định

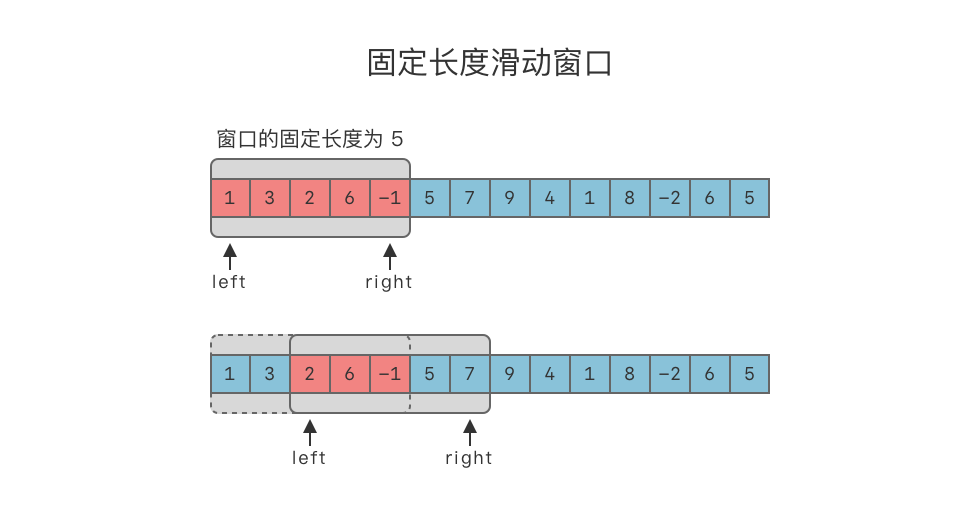
Thuật toán cửa sổ trượt độ dài cố định (Fixed Length Sliding Window): Duy trì một cửa sổ có độ dài cố định trên một mảng / chuỗi đã cho. Có thể thực hiện các hoạt động trượt, co giãn và duy trì giải pháp tối ưu trên cửa sổ.

3.1 Các bước thuật toán cửa sổ trượt độ dài cố định

Giả sử kích thước cửa sổ cố định là $window\underline{}size$ .

Sử dụng hai con trỏ $left$ và $right$ . Ban đầu, $left$ và $right$ đều trỏ đến phần tử đầu tiên của mảng, tức là $left = 0$ và $right = 0$ . Khoảng $[left, right]$ được gọi là "cửa sổ".
Khi cửa sổ chưa đạt đến kích thước $window\underline{}size$ , tiếp tục di chuyển $right$ , đưa $window\underline{}size$ phần tử đầu tiên của mảng vào cửa sổ, tức là window.append(nums[right]).
Khi cửa sổ đạt đến kích thước $window\underline{}size$ $w in d o w s i ze$ , tức là thỏa mãn điều kiện right - left + 1 >= window_size, kiểm tra xem các phần tử liên tiếp trong cửa sổ có thỏa mãn điều kiện giới hạn của bài toán không.
1. Nếu thỏa mãn, cập nhật giải pháp tối ưu theo yêu cầu.
2. Sau đó, di chuyển $left$ sang phải để thu nhỏ kích thước cửa sổ, tức là left += 1, đảm bảo kích thước cửa sổ luôn là $window\underline{}size$ .
Di chuyển $right$ sang phải, đưa phần tử vào cửa sổ, tức là window.append(nums[right]).
Lặp lại các bước 2-4 cho đến khi $right$ đến cuối mảng.

3.2 Mẫu mã code cửa sổ trượt độ dài cố định

left = 0
right = 0

while right < len(nums):
    window.append(nums[right])
    
    # Khi vượt quá kích thước cửa sổ, thu nhỏ cửa sổ, duy trì kích thước cửa sổ luôn là window_size
    if right - left + 1 >= window_size:
        # ... Duy trì giải pháp
        window.popleft()
        left += 1
    
    # Di chuyển sang phải để tăng kích thước cửa sổ
    right += 1

Dưới đây chúng ta sẽ trình bày cách sử dụng cửa sổ trượt độ dài cố định để giải quyết vấn đề cụ thể.

3.3 Số lượng mảng con có độ dài K và trung bình lớn hơn hoặc bằng ngưỡng

3.3.1 Liên kết đề bài

1343. Số lượng mảng con có độ dài K và trung bình lớn hơn hoặc bằng ngưỡng - LeetCode

3.3.2 Tóm tắt đề bài

Mô tả: Cho một mảng số nguyên $arr$ và hai số nguyên $k$ và $threshold$ .

Yêu cầu: Trả về số lượng mảng con có độ dài $k$ và trung bình lớn hơn hoặc bằng $threshold$ .

Giải thích:

$1 \le arr.length \le 10^5$ .
$1 \le arr[i] \le 10^4$ .
$1 \le k \le arr.length$ .
$0 \le threshold \le 10^4$ .

Ví dụ:

Ví dụ 1:

Input: arr = [2,2,2,2,5,5,5,8], k = 3, threshold = 4
Output: 3
Giải thích: Có 3 mảng con [2,5,5], [5,5,5] và [5,5,8] có trung bình lớn hơn hoặc bằng 4. Các mảng con khác có độ dài 3 có trung bình nhỏ hơn 4.

Ví dụ 2:

Input: arr = [11,13,17,23,29,31,7,5,2,3], k = 3, threshold = 5
Output: 6
Giải thích: 6 mảng con đầu tiên có độ dài 3 có trung bình lớn hơn 5. Lưu ý rằng trung bình không phải là số nguyên.

3.3.3 Ý tưởng giải quyết

Ý tưởng 1: Cửa sổ trượt (độ dài cố định)

Đây là một bài toán cửa sổ trượt với độ dài cố định. Kích thước cửa sổ là $k$ . Cách làm cụ thể như sau:

Sử dụng biến $ans$ để duy trì số lượng mảng con thỏa mãn yêu cầu.
Sử dụng biến $window\underline{}sum$ để duy trì tổng các phần tử trong cửa sổ.
Khởi tạo $left$ và $right$ đều trỏ đến phần tử đầu tiên của mảng, tức là $left = 0$ và $right = 0$ .
Di chuyển $right$ sang phải, đưa $k$ phần tử đầu tiên của mảng vào cửa sổ, tức là window_sum += arr[right].
Khi số lượng phần tử trong cửa sổ là $k$ $k$ , tức là thỏa mãn điều kiện right - left + 1 >= k, kiểm tra xem tổng và trung bình của các phần tử liên tiếp trong cửa sổ có lớn hơn hoặc bằng ngưỡng $threshold$ $t h res h o l d$ không.
1. Nếu thỏa mãn, tăng giá trị của $ans$ lên $1$ .
2. Sau đó, di chuyển $left$ sang phải để thu nhỏ kích thước cửa sổ, tức là left += 1, đảm bảo kích thước cửa sổ luôn là $k$ .
Lặp lại các bước 4-5 cho đến khi $right$ đến cuối mảng.
Trả về giá trị của $ans$ .

Ý tưởng 1: Code

class Solution:
    def numOfSubarrays(self, arr: List[int], k: int, threshold: int) -> int:
        left = 0
        right = 0
        window_sum = 0
        ans = 0

        while right < len(arr):
            window_sum += arr[right]
            
            if right - left + 1 >= k:
                if window_sum >= k * threshold:
                    ans += 1
                window_sum -= arr[left]
                left += 1

            right += 1

        return ans

Ý tưởng 1: Phân tích độ phức tạp

Độ phức tạp thời gian: $O(n)$ .
Độ phức tạp không gian: $O(n)$ .

4. Cửa sổ trượt độ dài không cố định

4.1 Bước thuật toán cửa sổ trượt độ dài không cố định

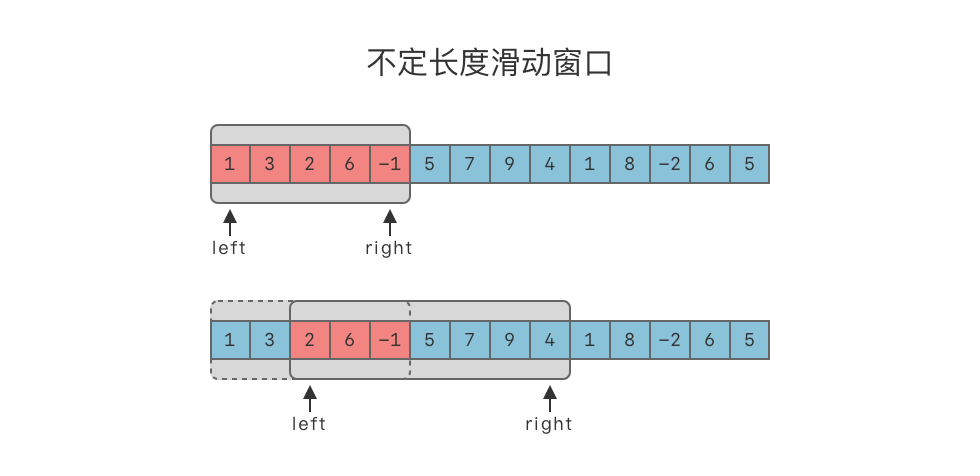
Sử dụng hai con trỏ $left$ và $right$ . Ban đầu, $left$ và $right$ đều trỏ đến phần tử đầu tiên của mảng. Tức là $left = 0$ và $right = 0$ . Khoảng $[left, right]$ được gọi là "cửa sổ".
Thêm phần tử ở vị trí $right$ vào cửa sổ, tức là window.append(s[right]).
Tiếp tục di chuyển $right$ sang phải để tăng kích thước cửa sổ, tức là right += 1. Cho đến khi các phần tử liên tiếp trong cửa sổ thỏa mãn yêu cầu.
Khi đạt được điều kiện, dừng việc tăng kích thước cửa sổ. Tiếp tục di chuyển $left$ sang phải để thu nhỏ cửa sổ, tức là window.popleft(s[left]).
Tiếp tục di chuyển $left$ sang phải để thu nhỏ cửa sổ, tức là left += 1. Cho đến khi các phần tử liên tiếp trong cửa sổ không còn thỏa mãn yêu cầu.
Lặp lại các bước 2-5 cho đến khi $right$ đến cuối mảng.

4.2 Mẫu mã code cửa sổ trượt độ dài không cố định

left = 0
right = 0

while right < len(nums):
    window.append(nums[right])
    
    while cửa sổ cần thu nhỏ:
        # ... Cập nhật giải pháp
        window.popleft()
        left += 1
    
    # Di chuyển sang phải để tăng kích thước cửa sổ
    right += 1

4.3 Dãy con không chứa ký tự lặp

4.3.1 Liên kết đề bài

3. Dãy con không chứa ký tự lặp - LeetCode

4.3.2 Tóm tắt đề bài

Mô tả: Cho một chuỗi $s$ .

Yêu cầu: Tìm độ dài của dãy con dài nhất trong $s$ mà không chứa ký tự lặp.

Giải thích:

$0 \le s.length \le 5 * 10^4$ .
$s$ chỉ gồm các ký tự chữ cái, số, dấu cách và ký tự đặc biệt.

Ví dụ:

Ví dụ 1:

Input: s = "abcabcbb"
Output: 3 
Giải thích: Dãy con dài nhất không chứa ký tự lặp là "abc" với độ dài là 3.

Ví dụ 2:

Input: s = "bbbbb"
Output: 1
Giải thích: Dãy con dài nhất không chứa ký tự lặp là "b" với độ dài là 1.

4.3.3 Ý tưởng giải quyết

Ý tưởng 1: Cửa sổ trượt (độ dài không cố định)

Sử dụng cửa sổ trượt $window$ để ghi nhận số lượng ký tự không lặp lại, $window$ là một từ điển.

Khởi tạo hai con trỏ $left$ và $right$ , ban đầu $left$ và $right$ đều trỏ đến vị trí đầu tiên của chuỗi, tức là $left = 0$ và $right = 0$ .
Di chuyển $right$ sang phải, thêm ký tự $s[right]$ vào cửa sổ hiện tại $window$ và ghi nhận số lượng ký tự không lặp lại.
Nếu số lượng ký tự không lặp lại trong cửa sổ $window$ vượt quá $1$ , tức là $window[s[right]] > 1$ , tiếp tục di chuyển $left$ sang phải để thu nhỏ cửa sổ và cập nhật lại số lượng ký tự không lặp lại.
Cập nhật độ dài dãy con không chứa ký tự lặp dài nhất. Tiếp tục di chuyển $right$ sang phải cho đến khi $right \ge len(s)$ .
Trả về độ dài của dãy con không chứa ký tự lặp dài nhất.

Ý tưởng 1: Code

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        left = 0
        right = 0
        window = dict()
        ans = 0

        while right < len(s):
            if s[right] not in window:
                window[s[right]] = 1
            else:
                window[s[right]] += 1

            while window[s[right]] > 1:
                window[s[left]] -= 1
                left += 1

            ans = max(ans, right - left + 1)
            right += 1

        return ans

Sử dụng thư viện defaultdict để từ dict có giá trị mặc định và rút gọn code:

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        left, right, ans = 0, 0, 0
        window = defaultdict(int)
        
        while right < len(s):
            window[s[right]] += 1

            while window[s[right]] > 1:
                window[s[left]] -= 1
                left += 1
            
            ans = max(ans, right - left + 1)
            right += 1

        return ans

Ý tưởng 1: Phân tích độ phức tạp

Độ phức tạp thời gian: $O(n)$ .
Độ phức tạp không gian: $O(| \sum |)$ . Ở đây, $\sum$ đại diện cho tập ký tự và $| \sum |$ đại diện cho kích thước của tập ký tự.

4.4 Độ dài mảng con nhỏ nhất

4.4.1 Liên kết đề bài

209. Độ dài mảng con nhỏ nhất - LeetCode

4.4.2 Tóm tắt đề bài

Mô tả: Cho một mảng $nums$ chỉ chứa các số nguyên dương và một số nguyên dương $target$ .

Yêu cầu: Tìm mảng con liên tiếp có tổng lớn hơn hoặc bằng $target$ và có độ dài nhỏ nhất trong mảng $nums$ . Trả về độ dài của mảng con đó. Nếu không có mảng con thỏa mãn, trả về $0$ .

Giải thích:

$1 \le target \le 10^9$ .
$1 \le nums.length \le 10^5$ .
$1 \le nums[i] \le 10^5$ .

Ví dụ:

Ví dụ 1:

Input: target = 7, nums = [2,3,1,2,4,3]
Output: 2
Giải thích: Mảng con [4,3] có tổng là 7 và có độ dài nhỏ nhất thỏa mãn yêu cầu.

Ví dụ 2:

Input: target = 4, nums = [1,4,4]
Output: 1

4.4.3 Ý tưởng giải quyết

Ý tưởng 1: Cửa sổ trượt (độ dài không cố định)

Cách tiếp cận trực tiếp nhất là sử dụng phương pháp thử tất cả các trường hợp, có độ phức tạp $O(n^2)$ . Tuy nhiên, chúng ta có thể sử dụng phương pháp cửa sổ trượt để giải quyết vấn đề trong phạm vi $O(n)$ .

Sử dụng cửa sổ trượt để ghi nhận tổng của mảng con liên tiếp, đặt hai con trỏ $left$ và $right$ để chỉ định biên trái và biên phải của cửa sổ, đảm bảo tổng trong cửa sổ lớn hơn hoặc bằng $target$ .

Ban đầu, $left$ và $right$ đều trỏ đến vị trí đầu tiên của mảng, tức là $left = 0$ và $right = 0$ .
Di chuyển $right$ sang phải, thêm phần tử ở vị trí $right$ vào tổng hiện tại của cửa sổ $window\underline{}sum$ .
Nếu $window\underline{}sum \ge target$ , tiếp tục di chuyển $left$ sang phải để thu nhỏ cửa sổ và cập nhật lại tổng hiện tại của cửa sổ, cho đến khi $window\underline{}sum < target$ .
Tiếp tục di chuyển $right$ sang phải cho đến khi $right \ge len(nums)$ .
Trả về độ dài của mảng con có tổng lớn nhất là kết quả.

Ý tưởng 1: Code

class Solution:
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        ans = len(nums) + 1
        left = 0
        right = 0
        window_sum = 0

        while right < len(nums):
            window_sum += nums[right]

            while window_sum >= target:
                ans = min(ans, right - left + 1)
                window_sum -= nums[left]
                left += 1

            right += 1

        return ans if ans != len(nums) + 1 else 0

Ý tưởng 1: Phân tích độ phức tạp

Độ phức tạp thời gian: $O(n)$ .
Độ phức tạp không gian: $O(1)$ .

4.5 Số lượng mảng con có tích nhỏ hơn K

4.5.1 Liên kết đề bài

713. Số lượng mảng con có tích nhỏ hơn K - LeetCode

4.5.2 Tóm tắt đề bài

Mô tả: Cho một mảng số nguyên dương $nums$ và một số nguyên dương $k$ .

Yêu cầu: Tìm số lượng mảng con liên tiếp trong mảng $nums$ có tích nhỏ hơn $k$ .

Giải thích:

$1 \le nums.length \le 3 * 10^4$ .
$1 \le nums[i] \le 1000$ .
$0 \le k \le 10^6$ .

Ví dụ:

Ví dụ 1:

Input: nums = [10,5,2,6], k = 100
Output: 8
Giải thích: Có 8 mảng con có tích nhỏ hơn 100: [10]、[5]、[2],、[6]、[10,5]、[5,2]、[2,6]、[5,2,6]。Cần lưu ý rằng [10,5,2] không phải là mảng con có tích nhỏ hơn 100.

Ví dụ 2:

Input: nums = [1,2,3], k = 0
Output: 0

4.5.3 Ý tưởng giải quyết

Ý tưởng 1: Cửa sổ trượt (độ dài không cố định)

Đặt hai con trỏ $left$ và $right$ để chỉ định biên trái và biên phải của cửa sổ trượt, đảm bảo tích của tất cả các số trong cửa sổ $window\underline{}product$ nhỏ hơn $k$ . Sử dụng $window\underline{}product$ để ghi nhận tích hiện tại của cửa sổ, sử dụng $count$ để ghi nhận số lượng mảng con thỏa mãn yêu cầu.
Ban đầu, $left$ và $right$ đều trỏ đến vị trí đầu tiên của mảng, tức là $left = 0$ và $right = 0$ .
Di chuyển $right$ sang phải, thêm phần tử ở vị trí $right$ vào tích hiện tại của cửa sổ $window\underline{}product$ .
Nếu $window\underline{}product \ge k$ ，tiếp tục di chuyển $left$ sang phải để thu nhỏ cửa sổ và cập nhật lại tích hiện tại của cửa sổ, cho đến khi $window\underline{}product < k$ 。
Ghi nhận số lượng mảng con thỏa mãn yêu cầu bằng cách cộng dồn $(right - left + 1)$ ，tiếp tục di chuyển $right$ sang phải cho đến khi $right \ge len(nums)$ 。
Trả về số lượng mảng con thỏa mãn yêu cầu.

Ý tưởng 1: Mã giả

class Solution:
    def numSubarrayProductLessThanK(self, nums: List[int], k: int) -> int:
        if k <= 1:
            return 0

        size = len(nums)
        left = 0
        right = 0
        window_product = 1
        
        count = 0
        
        while right < size:
            window_product *= nums[right]

            while window_product >= k:
                window_product /= nums[left]
                left += 1

            count += (right - left + 1)
            right += 1
            
        return count

Ý tưởng 1: Phân tích độ phức tạp

Độ phức tạp thời gian: $O(n)$ .
Độ phức tạp không gian: $O(1)$ .