String Basic

1. Giới thiệu về chuỗi

Chuỗi (String): Được viết tắt là "str", là một chuỗi hữu hạn gồm một hoặc nhiều ký tự. Thường được ký hiệu là .

Dưới đây là một số khái niệm quan trọng liên quan đến chuỗi.

Tên chuỗi: Trong định nghĩa chuỗi, "s" là tên của chuỗi.
Giá trị của chuỗi: Chuỗi được tạo thành từ chuỗi các ký tự và thường được đặt trong dấu ngoặc kép.
Biến ký tự: Mỗi vị trí trong chuỗi là một biến ký tự. Ký tự có thể là chữ cái, số hoặc ký tự khác. là vị trí của ký tự đó trong chuỗi.
Độ dài của chuỗi: Số lượng ký tự trong chuỗi được gọi là độ dài của chuỗi.
Chuỗi rỗng: Chuỗi không chứa ký tự nào được gọi là "chuỗi rỗng". Độ dài của chuỗi rỗng là 0 và được biểu diễn bằng "".
Chuỗi con: Một chuỗi con là một dãy liên tiếp các ký tự trong chuỗi ban đầu. Chuỗi con có thể là chuỗi con gồm một ký tự, hai ký tự hoặc nhiều ký tự. Có hai loại chuỗi con đặc biệt: chuỗi con bắt đầu từ vị trí 0 và có độ dài k được gọi là "tiền tố". Chuỗi con kết thúc tại vị trí n - 1 và có độ dài k được gọi là "hậu tố".
Chuỗi chính: Chuỗi chứa chuỗi con được gọi là "chuỗi chính".

Dưới đây là một ví dụ để minh họa:

str = "Hello World"

Trong đoạn mã ví dụ trên, str là tên biến chuỗi, "Hello World" là giá trị của chuỗi đó, và độ dài của chuỗi là 11. Chuỗi được biểu diễn như hình dưới đây: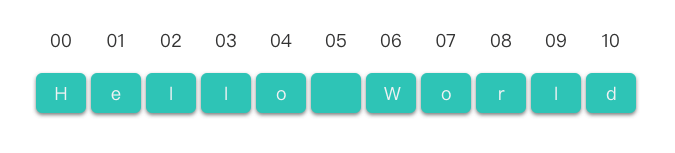

Có thể thấy, chuỗi và mảng có nhiều điểm tương đồng. Ví dụ, cùng sử dụng cú pháp tên[thứ tự] để truy cập vào một ký tự.

Lý do chúng ta đặc biệt nói về chuỗi là vì:

Các phần tử dữ liệu trong chuỗi đều là ký tự, có cấu trúc đơn giản, nhưng có thể có quy mô lớn.
Thường xuyên cần xem xét chuỗi như một thực thể duy nhất để sử dụng và xử lý. Đối tượng hoạt động thường không phải là một phần tử dữ liệu cụ thể, mà là một tập hợp dữ liệu (toàn bộ chuỗi hoặc chuỗi con).
Thường xuyên cần xem xét các hoạt động giữa nhiều chuỗi. Ví dụ: nối chuỗi, so sánh chuỗi.

Dựa trên đặc điểm của chuỗi, chúng ta có thể chia các vấn đề liên quan đến chuỗi thành các loại sau:

Vấn đề khớp chuỗi.
Vấn đề liên quan đến chuỗi con.
Vấn đề tiền tố / hậu tố.
Vấn đề chuỗi đối xứng.
Vấn đề hoán vị tiếp theo.

2. So sánh chuỗi

2.1 Các phép so sánh chuỗi

So sánh hai số rất dễ, ví dụ như 1 < 2. Tuy nhiên, so sánh hai chuỗi có phức tạp hơn một chút. So sánh hai chuỗi phụ thuộc vào thứ tự các ký tự trong chuỗi.

Ví dụ, cho hai chuỗi str1 = "abc" và str2 = "acc". Cả hai chuỗi đều có ký tự đầu tiên là a, nhưng ký tự thứ hai, vì ký tự b đứng trước ký tự c, nên ta có thể nói "abc" < "acc" hoặc str1 < str2.

So sánh hai chuỗi dựa trên thứ tự các ký tự trong chuỗi. So sánh chuỗi str1 và str2 theo các quy tắc sau:

Bắt đầu từ vị trí 0 của hai chuỗi, so sánh lần lượt các ký tự tại vị trí tương ứng.
- Nếu ký tự str1[i] có mã ký tự bằng với ký tự str2[i], tiếp tục so sánh ký tự tiếp theo.
- Nếu ký tự str1[i] có mã ký tự nhỏ hơn ký tự str2[i], ta có str1 < str2. Ví dụ: "abc" < "acc".
- Nếu ký tự str1[i] có mã ký tự lớn hơn ký tự str2[i], ta có str1 > str2. Ví dụ: "bcd" > "bad".
Nếu so sánh đến cuối chuỗi mà một chuỗi còn lại, ta có:
- Nếu độ dài của chuỗi str1 nhỏ hơn độ dài của chuỗi str2, tức là len(str1) < len(str2), ta có str1 < str2. Ví dụ: "abc" < "abcde".
- Nếu độ dài của chuỗi str1 lớn hơn độ dài của chuỗi str2, tức là len(str1) > len(str2), ta có str1 > str2. Ví dụ: "abcde" > "abc".
Nếu các ký tự tại mỗi vị trí trong hai chuỗi đều giống nhau và độ dài của hai chuỗi bằng nhau, ta có str1 == str2. Ví dụ: "abcd" == "abcd".

Dựa trên quy tắc trên, ta có thể định nghĩa một phương thức strcmp và quy ước:

Khi str1 < str2, phương thức strcmp trả về -1.
Khi str1 == str2, phương thức strcmp trả về 0.
Khi str1 > str2, phương thức strcmp trả về 1.

Mã giả của phương thức strcmp như sau:

def strcmp(str1, str2):
    index1, index2 = 0, 0
    while index1 < len(str1) and index2 < len(str2):
        if ord(str1[index1]) == ord(str2[index2]):
            index1 += 1
            index2 += 1
        elif ord(str1[index1]) < ord(str2[index2]):
            return -1
        else:
            return 1
    
    if len(str1) < len(str2):
        return -1
    elif len(str1) > len(str2):
        return 1
    else:
        return 0

Quy tắc so sánh chuỗi trên có một chút phức tạp. Tuy nhiên, một ví dụ đơn giản về so sánh chuỗi là "tra từ điển tiếng Anh". Trong từ điển tiếng Anh, các từ đứng trước sẽ nhỏ hơn các từ đứng sau. Nếu ta coi mỗi từ trong từ điển tiếng Anh là một chuỗi, quá trình tìm kiếm từ trong từ điển thực chất là quá trình so sánh chuỗi.

2.2 Mã hóa ký tự trong chuỗi

Trong phần trước, chúng ta đã đề cập đến mã hóa ký tự và giới thiệu một số tiêu chuẩn mã hóa ký tự phổ biến trong chuỗi.

Ví dụ, chúng ta có thể sử dụng mã hóa ASCII cho các ký tự thông dụng trong máy tính. Ban đầu, một bảng mã ASCII gồm 127 ký tự được đưa vào hệ thống máy tính. Bảng mã ASCII bao gồm các ký tự chữ cái in hoa, chữ cái thường, số và một số ký tự đặc biệt. Mỗi ký tự tương ứng với một mã, ví dụ như mã của chữ cái in hoa A là 65, mã của chữ cái thường a là 97.

Mã hóa ASCII có thể giải quyết các ngôn ngữ chủ yếu sử dụng tiếng Anh, nhưng không đáp ứng được mã hóa tiếng Việt. Trên thế giới có hàng trăm ngôn ngữ và chữ viết khác nhau, mỗi quốc gia có tiêu chuẩn mã hóa riêng, dẫn đến xung đột không thể tránh khỏi. Do đó, đã có mã hóa Unicode. Mã hóa Unicode phổ biến nhất là mã hóa UTF-8, mã hóa UTF-8 mã hóa một ký tự Unicode thành 1 đến 6 byte dựa trên giá trị số, các chữ cái tiếng Anh thông thường được mã hóa thành 1 byte, trong khi các ký tự tiếng Việt thường được mã hóa thành 2 byte, nếu có dấu thì mã hoá thành 3 byte.

3.1 Cấu trúc lưu trữ tuần tự của chuỗi

Giống như cấu trúc lưu trữ tuần tự của danh sách tuyến tính, cấu trúc lưu trữ tuần tự của chuỗi cũng sử dụng một nhóm các đơn vị lưu trữ có địa chỉ liên tiếp để lưu trữ từng ký tự trong chuỗi. Theo kích thước được định nghĩa trước, mỗi biến chuỗi được định nghĩa sẽ được cấp phát một khu vực lưu trữ có độ dài cố định. Thông thường, một mảng cố định được sử dụng để định nghĩa.

Cấu trúc lưu trữ tuần tự của chuỗi được minh họa như hình dưới đây.

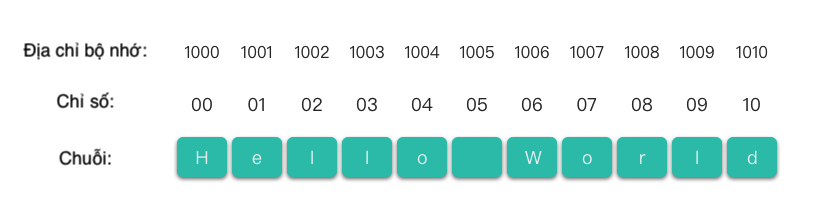
Như hình trên, mỗi phần tử ký tự trong cấu trúc lưu trữ tuần tự của chuỗi có chỉ số của riêng nó, chỉ số bắt đầu từ 0 và kết thúc tại độ dài chuỗi - 1. Mỗi chỉ số trong chuỗi có một phần tử ký tự tương ứng.

Tương tự như mảng, chuỗi cũng hỗ trợ truy cập ngẫu nhiên. Nghĩa là chuỗi có thể được xác định vị trí lưu trữ của một phần tử ký tự cụ thể dựa trên chỉ số.

3.2 Cấu trúc lưu trữ liên kết của chuỗi

Chuỗi cũng có thể được lưu trữ bằng cấu trúc lưu trữ liên kết, tức là sử dụng một danh sách liên kết tuyến tính để lưu trữ một chuỗi. Mỗi nút liên kết của chuỗi bao gồm một biến data để lưu trữ ký tự và một biến con trỏ next để trỏ đến nút liên kết tiếp theo. Như vậy, một chuỗi có thể được biểu diễn bằng một danh sách liên kết tuyến tính.

Trong cấu trúc lưu trữ liên kết của chuỗi, mỗi nút liên kết có thể chỉ chứa một ký tự hoặc nhiều ký tự. Thông thường, độ dài ký tự của nút liên kết là 1 hoặc 4, điều này để tránh lãng phí không gian. Khi độ dài ký tự của nút liên kết là 4, do độ dài chuỗi không nhất thiết là bội số của 4, nên biến data của nút liên kết cuối cùng có thể không được lấp đầy. Chúng ta có thể sử dụng ký tự đặc biệt # hoặc ký tự đặc biệt khác không thuộc bộ ký tự để điền vào.

Cấu trúc lưu trữ liên kết của chuỗi được minh họa như hình dưới đây.

Như hình trên, cấu trúc lưu trữ liên kết của chuỗi kết nối một nhóm các đơn vị lưu trữ bất kỳ. Mối quan hệ logic giữa các nút liên kết được phản ánh thông qua con trỏ.

3.3 Chuỗi trong các ngôn ngữ khác nhau

Chuỗi trong ngôn ngữ C được lưu trữ dưới dạng mảng ký tự kết thúc bằng ký tự null \0. Ký tự null \0 được sử dụng để đánh dấu kết thúc chuỗi. Thư viện chuẩn của ngôn ngữ C string.h cung cấp các hàm để xử lý chuỗi.
Trong ngôn ngữ C++, ngoài việc cung cấp chuỗi kiểu C, còn có lớp string. Lớp string xử lý chuỗi rất tiện lợi và hoàn toàn có thể thay thế mảng ký tự hoặc con trỏ chuỗi trong ngôn ngữ C.
Trong thư viện chuẩn của ngôn ngữ Java cũng cung cấp lớp String để làm việc với chuỗi.
Trong ngôn ngữ Python, chuỗi được biểu diễn bằng đối tượng str. Đối tượng str là một loại đối tượng không thể thay đổi. Nghĩa là đối tượng chuỗi được tạo bằng kiểu str không thể thay đổi độ dài của chuỗi hoặc thay đổi hoặc xóa các ký tự trong chuỗi.

4. Vấn đề khớp chuỗi

Khớp chuỗi (String Matching): Còn được gọi là khớp mẫu (Pattern Matching). Có thể hiểu đơn giản là, cho trước chuỗi văn bản T và mẫu p, tìm kiếm chuỗi con p trong chuỗi văn bản T. Chuỗi văn bản T còn được gọi là chuỗi văn bản, chuỗi con p còn được gọi là mẫu (Pattern).

Trong vấn đề chuỗi, một trong những vấn đề quan trọng nhất là vấn đề khớp chuỗi. Dựa theo số lượng mẫu, chúng ta có thể chia vấn đề khớp chuỗi thành hai loại: "Vấn đề khớp chuỗi đơn" và "Vấn đề đa khớp mẫu".

4.1 Vấn đề khớp chuỗi đơn

Vấn đề khớp mẫu đơn (Single Pattern Matching): Cho trước một chuỗi văn bản $T = t_1t_2…t_n$ , và một mẫu cụ thể $p = p_1p_2…p_n$ . Yêu cầu tìm tất cả các vị trí xuất hiện của mẫu cụ thể $p$ trong chuỗi văn bản $T$ .

Có nhiều thuật toán để giải quyết vấn đề khớp mẫu đơn. Dựa vào cách tìm kiếm mẫu trong văn bản, chúng ta có thể chia thuật toán khớp mẫu đơn thành các loại sau:

Dựa trên phương pháp tìm kiếm tiền tố: Trong cửa sổ tìm kiếm, từ trước đến sau (theo hướng dương của văn bản), từng ký tự của văn bản được đọc vào một cách tuần tự, tìm kiếm tiền tố chung dài nhất giữa văn bản trong cửa sổ tìm kiếm và mẫu.
- Các thuật toán nổi tiếng như Knuth-Morris-Pratt (KMP) và Shift-Or sử dụng phương pháp này.
Dựa trên phương pháp tìm kiếm hậu tố: Trong cửa sổ tìm kiếm, từ sau đến trước (theo hướng âm của văn bản), từng ký tự của văn bản được đọc vào một cách tuần tự, tìm kiếm hậu tố chung dài nhất giữa văn bản trong cửa sổ tìm kiếm và mẫu. Sử dụng phương pháp này có thể bỏ qua một số ký tự văn bản, do đó có độ phức tạp thời gian trung bình dưới tuyến tính.
- Thuật toán nổi tiếng như Boyer-Moore và Horspool cũng như Sunday (phiên bản đơn giản của thuật toán Boyer-Moore) sử dụng phương pháp này.
Dựa trên phương pháp tìm kiếm chuỗi con: Trong cửa sổ tìm kiếm, từ sau đến trước (theo hướng âm của văn bản), từng ký tự của văn bản được đọc vào một cách tuần tự, tìm kiếm chuỗi con dài nhất trong văn bản trong cửa sổ tìm kiếm, đồng thời là chuỗi con của mẫu. Mặc dù phương pháp này cũng có độ phức tạp thời gian trung bình dưới tuyến tính, nhưng việc xác định tất cả các chuỗi con của mẫu là một vấn đề phức tạp.
- Rabin-Karp, Backward Dawg Matching (BDM), Backward Nondeterministic Dawg Matching (BNDM) và Backward Oracle Matching (BOM) đều sử dụng phương pháp này. Trong đó, Rabin-Karp sử dụng phương pháp tìm kiếm chuỗi con dựa trên băm.

4.2 Vấn đề đa khớp mẫu

Vấn đề khớp mẫu đa (Multi Pattern Matching): Cho trước một chuỗi văn bản $T = t_1t_2…t_n$ , và một tập hợp các mẫu $P = {p^1, p^2, … ,p^r}$ , trong đó mỗi mẫu $p^i$ là một chuỗi được định nghĩa trên bảng chữ cái hữu hạn $p^i = p^i_1p^i_2…p^i_n$ . Yêu cầu tìm tất cả các vị trí xuất hiện của tất cả các mẫu $p^i$ trong chuỗi văn bản $T$ .

Một số chuỗi trong tập hợp $P$ có thể là chuỗi con, tiền tố, hậu tố hoặc hoàn toàn giống nhau. Nếu sử dụng thuật toán khớp mẫu đơn để giải quyết vấn đề khớp mẫu đa, thì phải tìm kiếm $r$ lần. Điều này dẫn đến độ phức tạp thời gian tệ nhất $O(|P|)$ trong giai đoạn tiền xử lý và $O(r * n)$ trong giai đoạn tìm kiếm.

Nếu sử dụng thuật toán khớp mẫu đơn để giải quyết vấn đề khớp mẫu đa, thì dựa vào cách tìm kiếm mẫu trong văn bản, chúng ta cũng có thể chia thuật toán khớp mẫu đa thành ba loại sau:

Dựa trên phương pháp tìm kiếm tiền tố: Tìm kiếm từ trước đến sau (theo hướng dương của văn bản), từng ký tự của văn bản được đọc vào một cách tuần tự, sử dụng tự động hóa được xây dựng trên $P$ $P$ để nhận diện. Đối với mỗi vị trí văn bản, tính toán chuỗi dài nhất vừa là hậu tố của văn bản đã đọc, vừa là tiền tố của một mẫu trong $P$ $P$ .
- Thuật toán nổi tiếng như Aho-Corasick Automaton (AC Automaton) và Multiple Shift-And sử dụng phương pháp này.
Dựa trên phương pháp tìm kiếm hậu tố: Tìm kiếm từ sau đến trước (theo hướng âm của văn bản), tìm kiếm hậu tố của mẫu. Dựa vào vị trí xuất hiện tiếp theo của hậu tố để di chuyển vị trí văn bản hiện tại. Phương pháp này có thể bỏ qua một số ký tự văn bản, do đó có độ phức tạp thời gian trung bình dưới tuyến tính.
- Commentz-Walter, Set Horspool (phiên bản đơn giản của Commentz-Walter), Wu-Manber đều sử dụng phương pháp này.
Dựa trên phương pháp tìm kiếm chuỗi con: Tìm kiếm từ sau đến trước (theo hướng âm của văn bản), tìm kiếm chuỗi con dài nhất trong văn bản là chuỗi con của mẫu. Mặc dù phương pháp này cũng có độ phức tạp thời gian trung bình dưới tuyến tính, nhưng việc xác định tất cả các chuỗi con của mẫu là một vấn đề phức tạp.
- Multiple BNDM, Set Backward Dawg Matching (SBDM), Set Backward Oracle Matching (SBOM) đều sử dụng phương pháp này.

Cần lưu ý rằng, hầu hết các thuật toán khớp mẫu đa đều sử dụng một cấu trúc dữ liệu cơ bản: "Cây từ điển (Trie Tree)". Thuật toán nổi tiếng "Aho-Corasick Automaton (AC Automaton)" là kết hợp của thuật toán KMP và cấu trúc dữ liệu "Cây từ điển". Thuật toán AC Automaton cũng là một trong những thuật toán hiệu quả nhất trong vấn đề khớp mẫu đa.