Tìm kiếm nhị phân phần 2

3. Chi tiết của tìm kiếm nhị phân

Trong ví dụ trước, chúng ta đã hiểu được ý tưởng và mã của thuật toán tìm kiếm nhị phân. Tuy nhiên, khi thực sự giải quyết các bài toán tìm kiếm nhị phân, chúng ta cần xem xét nhiều chi tiết hơn. Dưới đây là một số vấn đề cần xem xét:

1. Vấn đề về phạm vi của khoảng：Khoảng cần tìm kiếm có phải là khoảng từ trái đóng đến phải đóng $[left, right]$ hay không, hay là khoảng từ trái đóng đến phải mở $[left, right)$?
2. Vấn đề về giá trị của $mid$: $mid = \lfloor \frac{left + right}{2} \rfloor$ hay $mid = \lfloor \frac{left + right + 1}{2} \rfloor$?
3. Điều kiện thoát khỏi vòng lặp: $left \le right$ hay $left < right$?
4. Lựa chọn phạm vi tìm kiếm: Làm thế nào để cập nhật $left$ và $right$ khi tìm kiếm trong khoảng $[left, right]$?

Chúng ta sẽ đi vào từng vấn đề một.

3.1 Vấn đề về phạm vi của khoảng tìm kiếm

Khoảng cần tìm kiếm có thể là khoảng từ trái đóng đến phải đóng $[left, right]$ hoặc khoảng từ trái đóng đến phải mở $[left, right)$.

• Khoảng từ trái đóng đến phải đóng: Ban đầu, $left = 0$ và $right = len(nums) - 1$.
  • $left$ là vị trí của phần tử đầu tiên trong mảng, $right$ là vị trí của phần tử cuối cùng trong mảng.
  • Khoảng $[left, right]$ bao gồm cả các điểm biên trái và phải.
• Khoảng từ trái đóng đến phải mở: Ban đầu, $left = 0$ và $right = len(nums)$.
  • $left$ là vị trí của phần tử đầu tiên trong mảng, $right$ là vị trí sau phần tử cuối cùng trong mảng.
  • Khoảng $[left, right)$ bao gồm điểm biên trái nhưng không bao gồm điểm biên phải.

Về cơ bản, việc sử dụng khoảng từ trái đóng đến phải đóng là cách viết đơn giản và dễ hiểu hơn. Vì vậy, tôi khuyến nghị: hãy luôn sử dụng khoảng từ trái đóng đến phải đóng.

3.2 Vấn đề về giá trị của $mid$

Trong thực tế, có hai công thức phổ biến để tính giá trị của $mid$:

1. mid = (left + right) // 2.
2. mid = (left + right + 1) // 2.

Trong cả hai công thức trên, // biểu thị "chia lấy phần nguyên" trong Python. Khi số lượng phần tử trong khoảng tìm kiếm là số lẻ, cả hai công thức đều cho kết quả là vị trí giữa của phần tử.

Khi số lượng phần tử trong khoảng tìm kiếm là số chẵn, công thức thứ nhất sẽ cho kết quả là vị trí giữa bên trái của phần tử, trong khi công thức thứ hai sẽ cho kết quả là vị trí giữa bên phải của phần tử.

20230906153409.png

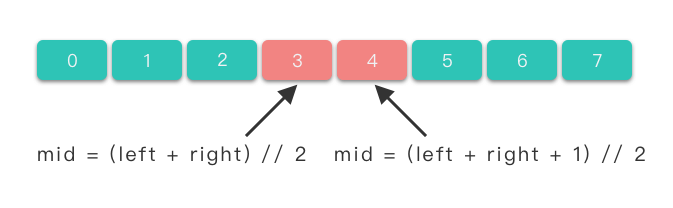
Hãy thử sử dụng cả hai công thức trên trong mã của 704. Binary Search và bạn sẽ thấy cả hai đều cho kết quả đúng. Tại sao lại như vậy?

Vì ý tưởng của thuật toán tìm kiếm nhị phân là: dựa trên việc chọn giá trị ở vị trí giữa mỗi lần để quyết định xem tiếp theo sẽ tìm kiếm trong khoảng nào. Mỗi lần chọn giá trị, không nhất thiết phải chọn giá trị ở vị trí giữa của khoảng, có thể chọn ở vị trí giữa bên trái, bên phải hoặc thậm chí ở một phần tư hoặc một phần năm của khoảng. Ví dụ: mid = (left + right) * 1 // 5 cũng hoàn toàn hợp lệ.

Tuy nhiên, thường thì việc chọn giá trị ở vị trí giữa của khoảng sẽ cho hiệu quả tốt nhất trong trường hợp trung bình. Đồng thời, cách viết này đơn giản nhất. Vì vậy, chúng ta thường chọn công thức đầu tiên. Tuy nhiên, trong một số trường hợp, chúng ta cần xem xét công thức thứ hai, chúng ta sẽ giải thích trong phần "4.2 Phương pháp loại trừ".

Ngoài hai công thức trên, chúng ta cũng thường thấy hai công thức sau:

1. mid = left + (right - left) // 2.
2. mid = left + (right - left + 1) // 2.

Thực chất, hai công thức này tương đương với hai công thức trước, có thể coi là cách viết khác của hai công thức trước. Cách viết này giúp tránh vấn đề tràn số nguyên (trong Python, số nguyên không bao giờ tràn, nhưng trong các ngôn ngữ khác có thể xảy ra tràn số nguyên).

Khi $left + right$ không vượt quá giá trị tối đa của kiểu số nguyên, cả hai cách viết đều không có vấn đề. Khi $left + right$ có thể vượt quá giá trị tối đa của kiểu số nguyên, nên sử dụng cách viết thứ hai. Vì vậy, để thống nhất và đơn giản hóa cách viết của thuật toán tìm kiếm nhị phân, tôi khuyến nghị sử dụng cách viết thứ hai:

1. mid = left + (right - left) // 2.
2. mid = left + (right - left + 1) // 2.

3.3 Điều kiện thoát khỏi vòng lặp

Có hai điều kiện kiểm tra để thoát khỏi vòng lặp while trong thuật toán tìm kiếm nhị phân:

1. left <= right.
2. left < right.

Chúng ta nên sử dụng điều kiện nào?

Hãy xem xét điều kiện nào sẽ làm cho vòng lặp thoát.

1. Nếu điều kiện là left <= right và phần tử cần tìm không có trong mảng đã sắp xếp, thì điều kiện thoát khỏi vòng lặp là left > right, tức là left == right + 1 và khoảng cần tìm kiếm trở thành $[right + 1, right]$, tức là không có phần tử trong khoảng cần tìm kiếm. Khi kết thúc vòng lặp, chúng ta có thể trả về $-1$ mà không cần kiểm tra điều kiện nữa.

   • Ví dụ: Khoảng $[3, 2]$, khi đó giới hạn trái lớn hơn giới hạn phải, ta có thể kết thúc vòng lặp và trả về $-1$.

2. Nếu điều kiện là left < right và phần tử cần tìm không có trong mảng đã sắp xếp, thì điều kiện thoát khỏi vòng lặp là left == right, tức là $[right, right]$. Khoảng này không rỗng, vẫn còn một phần tử trong khoảng cần tìm kiếm, chúng ta không thể chắc chắn rằng phần tử cần tìm không có trong khoảng này, nên khi kết thúc vòng lặp, nếu trả về $-1$ thì sẽ là sai.

   • Ví dụ: Khoảng $[2, 2]$, nếu phần tử $nums[2]$ chính là phần tử mục tiêu $target$ thì kết thúc vòng lặp và trả về $-1$ sẽ bỏ sót phần tử này.

Tuy nhiên, nếu chúng ta vẫn muốn sử dụng điều kiện left < right, chúng ta có thể thêm một lớp kiểm tra sau khi thoát khỏi vòng lặp, kiểm tra xem vị trí $left$ có trỏ đến phần tử mục tiêu không. Nếu có, trả về $left$; nếu không, trả về $-1$. Ví dụ:

# ...
    while left < right:
        # ...
    return left if nums[left] == target else -1

Ngoài ra, việc sử dụng điều kiện left < right có một lợi ích là khi thoát khỏi vòng lặp, chắc chắn là left == right, không cần kiểm tra xem nên trả về left hay right nữa.

3.4 Lựa chọn phạm vi tìm kiếm

Khi chọn phạm vi tìm kiếm, thường có ba cách viết:

1. left = mid + 1, right = mid - 1.
2. left = mid + 1, right = mid.
3. left = mid, right = mid - 1.

Chúng ta nên chọn phạm vi tìm kiếm như thế nào?

Đây là một khía cạnh khó của thuật toán tìm kiếm nhị phân. Viết sai dễ dẫn đến vòng lặp vô hạn hoặc không nhận được kết quả chính xác.

Điều này thực sự liên quan đến hai cách tiếp cận và ba cách viết của thuật toán tìm kiếm nhị phân.

• Cách tiếp cận 1: "Phương pháp trực tiếp" - Trả về kết quả ngay sau khi tìm thấy phần tử.
• Cách tiếp cận 2: "Phương pháp loại trừ" - Loại trừ phần tử mục tiêu không thể nằm trong khoảng.

Tiếp theo, chúng ta sẽ giải thích cả hai phương pháp.

4. Hai phương pháp tìm kiếm nhị phân

4.1 Phương pháp trực tiếp

Ý tưởng phương pháp trực tiếp: Một khi chúng ta tìm thấy phần tử trong vòng lặp, chúng ta sẽ trả về kết quả ngay lập tức.

Phương pháp này khá đơn giản, thực ra chúng ta đã sử dụng nó trong bài viết trước về "Tìm kiếm nhị phân cơ bản - 704. Binary Search" rồi. Dưới đây là ý tưởng và mã code:

Ý tưởng 1: Phương pháp trực tiếp

1. Đặt giới hạn trái và phải của mảng là hai đầu mút, tức là $left = 0$ và $right = len(nums) - 1$, đại diện cho phạm vi tìm kiếm là $[left, right]$ (phạm vi kín bên trái và phải).
2. Lấy vị trí giữa của hai đầu mút là $mid$, trước tiên so sánh giá trị tại vị trí giữa $nums[mid]$ với giá trị mục tiêu $target$.
   1. Nếu $target == nums[mid]$, trả về vị trí giữa ngay lập tức.
   2. Nếu $target > nums[mid]$, đặt đầu mút trái là $mid + 1$, sau đó tiếp tục tìm kiếm trong phạm vi bên phải $[mid + 1, right]$.
   3. Nếu $target < nums[mid]$, đặt đầu mút phải là $mid - 1$, sau đó tiếp tục tìm kiếm trong phạm vi bên trái $[left, mid - 1]$.
3. Nếu giới hạn trái lớn hơn giới hạn phải, phạm vi tìm kiếm thu hẹp lại thành rỗng, điều này có nghĩa là phần tử mục tiêu không tồn tại, lúc này trả về $-1$.

Mã code 1: Phương pháp trực tiếp

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
        
        # Tìm kiếm target trong phạm vi [left, right]
        while left <= right:
            # Lấy vị trí giữa của phạm vi
            mid = left + (right - left) // 2
            # Nếu tìm thấy giá trị mục tiêu, trả về vị trí giữa ngay lập tức
            if nums[mid] == target:
                return mid
            # Nếu nums[mid] nhỏ hơn giá trị mục tiêu, tiếp tục tìm kiếm trong phạm vi [mid + 1, right]
            elif nums[mid] < target:
                left = mid + 1
            # Nếu nums[mid] lớn hơn giá trị mục tiêu, tiếp tục tìm kiếm trong phạm vi [left, mid - 1]
            else:
                right = mid - 1
        # Không tìm thấy phần tử, trả về -1
        return -1

Chi tiết 1

• Phương pháp này trả về kết quả ngay lập tức khi tìm thấy phần tử trong vòng lặp.
• Điều kiện tiếp tục vòng lặp là left <= right.
• Nếu thoát khỏi vòng lặp, có nghĩa là phạm vi tìm kiếm đã thu hẹp lại thành rỗng và phần tử mục tiêu không tồn tại.

4.2 Phương pháp loại trừ

Ý tưởng phương pháp loại trừ: Trong vòng lặp, loại trừ các phạm vi mà phần tử mục tiêu nhất định không tồn tại.

Ý tưởng 2: Phương pháp loại trừ

1. Đặt giới hạn trái và phải của mảng là hai đầu mút, tức là $left = 0$ và $right = len(nums) - 1$, đại diện cho phạm vi tìm kiếm là $[left, right]$ (phạm vi kín bên trái và phải).
2. Lấy vị trí giữa của hai đầu mút là $mid$, so sánh phần tử mục tiêu và phần tử ở vị trí giữa, trước tiên loại trừ các phạm vi mà phần tử mục tiêu nhất định không tồn tại.
3. Tiếp tục tìm kiếm phần tử trong phạm vi còn lại, tiếp tục loại trừ các phạm vi mà phần tử mục tiêu nhất định không tồn tại.
4. Tiếp tục cho đến khi chỉ còn lại một phần tử trong phạm vi, sau đó kiểm tra xem phần tử đó có phải là phần tử mục tiêu không.

Dựa trên ý tưởng loại trừ, chúng ta có thể viết hai cách code.

Cách code 2: Phương pháp loại trừ

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
        
        # Tìm kiếm target trong phạm vi [left, right]
        while left < right:
            # Lấy vị trí giữa của phạm vi
            mid = left + (right - left) // 2
            # Nếu nums[mid] nhỏ hơn giá trị mục tiêu, loại trừ phạm vi không thể tồn tại target [left, mid], tiếp tục tìm kiếm trong phạm vi [mid + 1, right]
            if nums[mid] < target:
                left = mid + 1 
            # Nếu nums[mid] lớn hơn hoặc bằng giá trị mục tiêu, phần tử mục tiêu có thể tồn tại trong phạm vi [left, mid], tiếp tục tìm kiếm trong phạm vi [left, mid]
            else:
                right = mid
        # Kiểm tra xem phần tử còn lại trong phạm vi có phải là phần tử mục tiêu không, nếu không trả về -1
        return left if nums[left] == target else -1

Cách code 3: Phương pháp loại trừ

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
        
        # Tìm kiếm target trong phạm vi [left, right]
        while left < right:
            # Lấy vị trí giữa của phạm vi
            mid = left + (right - left + 1) // 2
            # Nếu nums[mid] lớn hơn giá trị mục tiêu, loại trừ phạm vi không thể tồn tại target [mid, right], tiếp tục tìm kiếm trong phạm vi [left, mid - 1]
            if nums[mid] > target:
                right = mid - 1 
            # Nếu nums[mid] nhỏ hơn hoặc bằng giá trị mục tiêu, phần tử mục tiêu có thể tồn tại trong phạm vi [mid, right], tiếp tục tìm kiếm trong phạm vi [mid, right]
            else:
                left = mid
        # Kiểm tra xem phần tử còn lại trong phạm vi có phải là phần tử mục tiêu không, nếu không trả về -1
        return left if nums[left] == target else -1

Ý tưởng 2: Chi tiết

• Điều kiện dừng vòng lặp là left < right. Điều này đảm bảo khi thoát khỏi vòng lặp, ta luôn có left == right, không cần phải kiểm tra xem nên trả về left hay right nữa. Lúc này chỉ cần kiểm tra xem nums[left] có phải là phần tử mục tiêu không.
• Trong thân vòng lặp, sau khi so sánh phần tử mục tiêu với phần tử ở giữa, ưu tiên loại bỏ khoảng không thể chứa phần tử mục tiêu, sau đó xác định khoảng tìm kiếm cho lần tìm kiếm tiếp theo từ khoảng còn lại.
• Sau khi loại bỏ khoảng không thể chứa phần tử mục tiêu, phần còn lại (phần else) thường không cần xem xét khoảng nữa, chỉ cần lấy khoảng đối diện với khoảng trước đó. Nếu khoảng trước đó là $[mid + 1, right]$ thì khoảng đối diện là $[left, mid]$. Nếu khoảng trước đó là $[left, mid - 1]$ thì khoảng đối diện là $[mid, right]$.
• Để tránh rơi vào vòng lặp vô hạn, khi khoảng bị chia thành 2 phần là $[left, mid - 1]$ và $[mid, right]$, giá trị của mid phải làm tròn lên. Tức là mid = left + (right - left + 1) // 2. Vì nếu chỉ còn 2 phần tử trong khoảng (lúc này right = left + 1), nếu vào nhánh left = mid, khoảng tìm kiếm sẽ không thu nhỏ, lần tìm kiếm tiếp theo vẫn là khoảng $[left, right]$, rơi vào vòng lặp vô hạn.
  • Ví dụ: Giả sử giới hạn trái left = 5, giới hạn phải right = 6, lúc này khoảng tìm kiếm là $[5, 6]$, mid = 5 + (6 - 5) // 2 = 5. Nếu vào nhánh left = mid, lần tìm kiếm tiếp theo khoảng vẫn là $[5, 6]$, không thu nhỏ khoảng, rơi vào vòng lặp vô hạn.
  • Trong trường hợp này, giá trị mid phải làm tròn lên, mid = 5 + (6 - 5 + 1) // 2 = 6. Nếu vào nhánh left = mid, lần tìm kiếm tiếp theo khoảng sẽ là $[6, 6]$.
• Về việc đặt giới hạn, có thể ghi nhớ như sau: chỉ cần nhìn vào left = mid thì làm tròn lên. Hoặc có thể ghi nhớ như sau:
  • left = mid + 1, right = mid và mid = left + (right - left) // 2 luôn đi cùng nhau.
  • right = mid - 1, left = mid và mid = left + (right - left + 1) // 2 luôn đi cùng nhau.

4.3 Phạm vi áp dụng hai ý tưởng

• Phương pháp trực tiếp: Vì điều kiện dừng là left <= right, nên đôi khi phải xem xét xem có trả về left hay right. Thân vòng lặp có 3 nhánh và luôn có một nhánh được sử dụng để thoát khỏi vòng lặp hoặc trả về trực tiếp. Ý tưởng này phù hợp để giải quyết các bài toán đơn giản. Tức là các phần tử cần tìm kiếm có tính chất đơn giản, mảng chỉ chứa các phần tử không trùng lặp và các trường hợp ==, > và < rất dễ viết.
• Phương pháp loại trừ: Phù hợp hơn với tư duy giảm thiểu của thuật toán tìm kiếm nhị phân. Mỗi lần loại bỏ khoảng không thể chứa phần tử mục tiêu, giúp giảm kích thước của vấn đề. Sau đó, tiếp tục tìm kiếm phần tử mục tiêu trong khoảng có thể tồn tại. Phương pháp này phù hợp để giải quyết các bài toán phức tạp hơn. Ví dụ: tìm một phần tử có thể không tồn tại trong mảng, tìm vấn đề ranh giới, có thể sử dụng phương pháp này.