Backtracking

1. Giới thiệu về thuật toán quay lui

Thuật toán quay lui (Backtracking): Là một thuật toán tìm kiếm theo phương pháp thử và sai, giúp tránh việc tìm kiếm không cần thiết. Thuật toán này sử dụng ý tưởng thử và sai để tìm kiếm giải pháp của một vấn đề. Khi tiến hành tìm kiếm, nếu gặp một bước không thỏa mãn điều kiện giải pháp hoặc cần thỏa mãn thêm điều kiện giải pháp, thuật toán sẽ quay lại bước trước đó (quay lui) để chọn lựa lại, điều này được gọi là "quay lui", và điểm trạng thái của một trạng thái thỏa mãn điều kiện quay lui được gọi là "điểm quay lui".

Đơn giản mà nói, thuật toán quay lui sử dụng một phương pháp "quay lui" khi gặp phải một bước không thể tiếp tục.

Thuật toán quay lui thường được thực hiện bằng cách sử dụng đệ quy đơn giản, trong quá trình quay lui có thể xảy ra hai trường hợp:

Tìm thấy một giải pháp có thể.
Sau khi thử tất cả các phương pháp khả dĩ, không tìm thấy giải pháp.

2. Hiểu thuật toán quay lui thông qua bài toán hoán vị

Lấy bài toán tìm tất cả các hoán vị của [1, 2, 3] làm ví dụ, chúng ta sẽ giải thích quá trình của thuật toán quay lui.

Chọn một hoán vị bắt đầu bằng số 1.
1. Chọn một hoán vị có số 2 ở vị trí thứ hai, sau đó chỉ có thể chọn số 3 ở vị trí cuối cùng. Hoán vị là [1, 2, 3].
2. Quay lui khỏi hoán vị có số 3 ở vị trí cuối cùng, sau đó quay lui khỏi hoán vị có số 2 ở vị trí thứ hai. Sau đó chọn một hoán vị có số 3 ở vị trí thứ hai, sau đó chỉ có thể chọn số 2 ở vị trí cuối cùng. Hoán vị là [1, 3, 2].
Quay lui khỏi hoán vị có số 2 ở vị trí cuối cùng, sau đó quay lui khỏi hoán vị có số 1 ở vị trí đầu tiên. Sau đó chọn một hoán vị bắt đầu bằng số 2.
1. Chọn một hoán vị có số 1 ở vị trí thứ hai, sau đó chỉ có thể chọn số 3 ở vị trí cuối cùng. Hoán vị là [2, 1, 3].
2. Quay lui khỏi hoán vị có số 3 ở vị trí cuối cùng, sau đó quay lui khỏi hoán vị có số 1 ở vị trí thứ hai. Sau đó chọn một hoán vị có số 3 ở vị trí thứ hai, sau đó chỉ có thể chọn số 1 ở vị trí cuối cùng. Hoán vị là [2, 3, 1].
Quay lui khỏi hoán vị có số 1 ở vị trí cuối cùng, sau đó quay lui khỏi hoán vị có số 3 ở vị trí thứ hai, sau đó quay lui khỏi hoán vị có số 2 ở vị trí đầu tiên. Sau đó chọn một hoán vị bắt đầu bằng số 3.
1. Chọn một hoán vị có số 1 ở vị trí thứ hai, sau đó chỉ có thể chọn số 2 ở vị trí cuối cùng. Hoán vị là [3, 1, 2].
2. Quay lui khỏi hoán vị có số 2 ở vị trí cuối cùng, sau đó quay lui khỏi hoán vị có số 1 ở vị trí thứ hai. Sau đó chọn một hoán vị có số 2 ở vị trí thứ hai, sau đó chỉ có thể chọn số 1 ở vị trí cuối cùng. Hoán vị là [3, 2, 1].

Tóm lại quá trình quay lui của hoán vị:

Liệt kê lần lượt từng số có thể xuất hiện ở mỗi vị trí, các số đã xuất hiện trước đó không thể xuất hiện lại.
Đối với mỗi vị trí, thực hiện các bước sau:
1. Chọn phần tử: Chọn một phần tử chưa xuất hiện từ danh sách phần tử có thể chọn.
2. Đệ quy tìm kiếm: Từ phần tử đã chọn, tiếp tục đệ quy tìm kiếm các vị trí còn lại, cho đến khi gặp điều kiện dừng, không tiếp tục tìm kiếm xuống nữa.
3. Quay lui: Quay lui từng bước để chọn một nhánh tìm kiếm khác. Đến khi hoàn thành việc duyệt qua tất cả các nhánh có thể.

Đối với quy trình quyết định trên, chúng ta cũng có thể sử dụng một cây quyết định để biểu diễn:

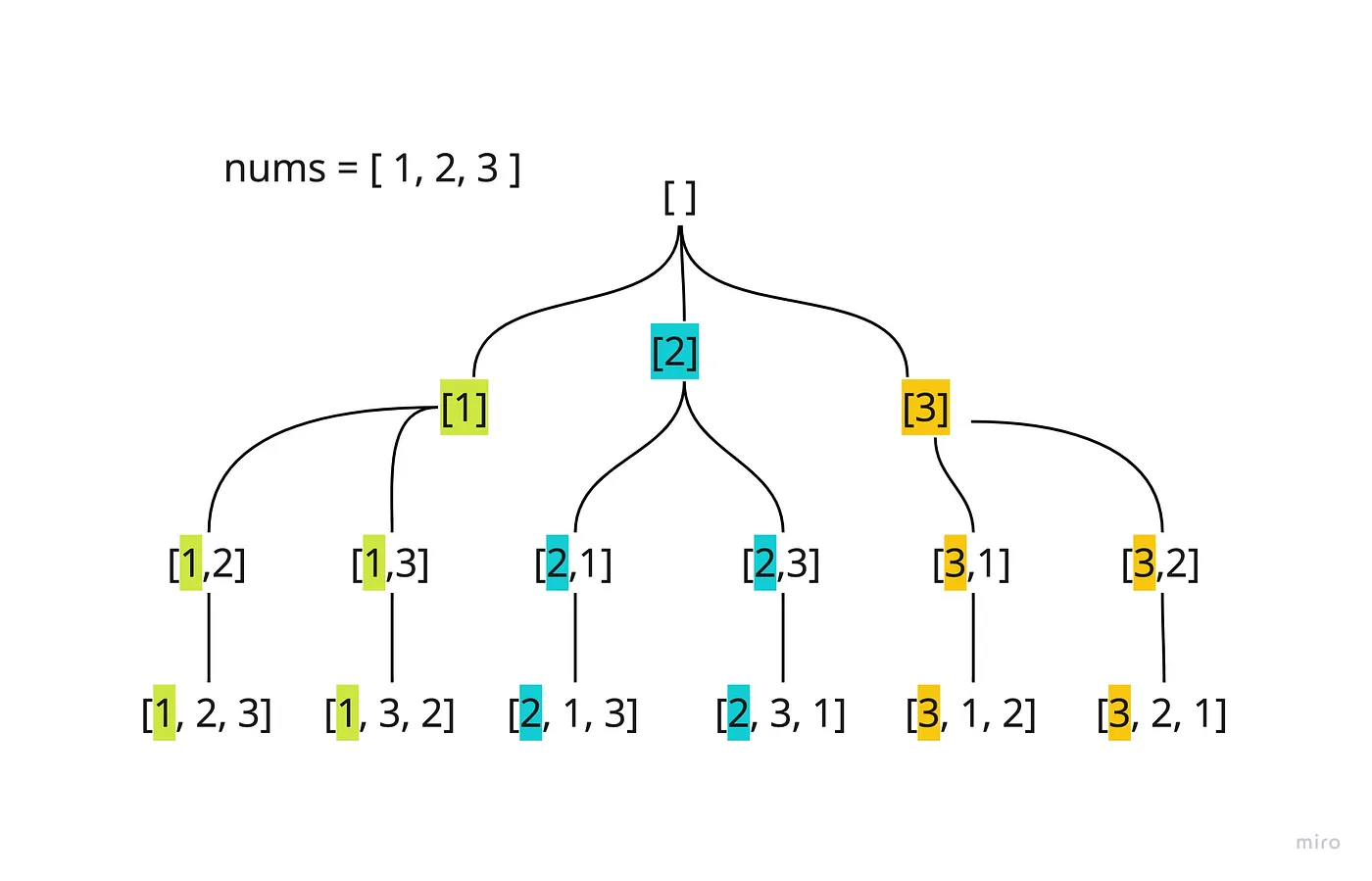
Từ cây quyết định của hoán vị, chúng ta có thể thấy:

Mỗi tầng có một hoặc nhiều nút khác nhau, những nút này cùng với các nhánh kết nối đại diện cho "các lựa chọn khác nhau".
Mỗi nút đại diện cho một "trạng thái" của việc giải quyết bài toán hoán vị, những trạng thái này được biểu diễn bằng "các giá trị khác nhau".
Mỗi lần đi xuống một tầng là chọn một "phần tử" từ danh sách các phần tử có thể chọn.
Khi một nhánh quyết định hoàn thành, chúng ta sẽ quay lui từng bước.
Mỗi lần quay lui một tầng, chúng ta sẽ xóa "phần tử" đã chọn khỏi "trạng thái hiện tại", quay trở lại trạng thái trước khi chưa chọn phần tử đó (hoặc nói cách khác là đặt lại trạng thái), từ đó tiếp tục khám phá các nhánh khác.

Dựa trên ý tưởng và cây quyết định trên, chúng ta có thể viết mã thuật toán quay lui cho hoán vị như sau (giả sử mảng đầu vào nums không chứa các phần tử trùng lặp):

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        res = []    # Lưu tất cả các kết quả thỏa mãn điều kiện
        path = []   # Lưu kết quả hiện tại thỏa mãn điều kiện
        def backtracking(nums):             # nums là danh sách phần tử có thể chọn
            if len(path) == len(nums):      # Nếu đã tìm thấy một kết quả thỏa mãn điều kiện
                res.append(path[:])         # Thêm kết quả hiện tại vào danh sách kết quả
                return

            for i in range(len(nums)):      # Liệt kê danh sách phần tử có thể chọn
                if nums[i] not in path:     # Chọn từ danh sách phần tử chưa xuất hiện trong đường đi
                    path.append(nums[i])    # Chọn phần tử
                    backtracking(nums)      # Đệ quy tìm kiếm
                    path.pop()              # Quay lui

        backtracking(nums)
        return res

3. Mẫu chung của thuật toán quay lui

Dựa trên code của thuật toán quay lui cho hoán vị, chúng ta có thể tạo ra một mẫu chung cho thuật toán quay lui. Code mẫu chung của thuật toán quay lui như sau:

res = []    # Lưu tất cả các kết quả thỏa mãn điều kiện
path = []   # Lưu kết quả hiện tại thỏa mãn điều kiện
def backtracking(nums):             # nums là danh sách phần tử có thể chọn
    if gặp điều kiện dừng:           # Nếu đã tìm thấy một kết quả thỏa mãn điều kiện
        res.append(path[:])         # Thêm kết quả hiện tại vào danh sách kết quả
        return

    for i in range(len(nums)):      # Liệt kê danh sách phần tử có thể chọn
        path.append(nums[i])        # Chọn phần tử
        backtracking(nums)          # Đệ quy tìm kiếm
        path.pop()                  # Quay lui

backtracking(nums)

Trong mẫu chung này, chúng ta cần điền vào các phần sau:

res: Một danh sách để lưu tất cả các kết quả thỏa mãn điều kiện.
path: Một danh sách để lưu kết quả hiện tại thỏa mãn điều kiện.
backtracking: Hàm đệ quy để thực hiện thuật toán quay lui.
nums: Danh sách các phần tử có thể chọn.
gặp điều kiện dừng: Điều kiện để dừng quá trình quay lui và thêm kết quả hiện tại vào danh sách kết quả.

Bằng cách sử dụng mẫu chung này, chúng ta có thể áp dụng thuật toán quay lui cho nhiều bài toán khác nhau chỉ bằng việc điền vào các phần tương ứng.

4. Ba bước cơ bản của thuật toán quay lui

Các bước giải quyết vấn đề bằng thuật toán quay lui trên mạng khá trừu tượng, ở đây chỉ là một giới thiệu đơn giản.

Xác định không gian giải pháp của vấn đề đã cho: Cần xác định không gian giải pháp phù hợp, bao gồm cách tổ chức giải pháp và ràng buộc rõ ràng.
- Cách tổ chức giải pháp: Tổ chức giải pháp thành một bộ n phần tử ${x_1, x_2, …, x_n}$ .
- Ràng buộc rõ ràng: Giới hạn phạm vi giá trị của các thành phần giải pháp, có thể kiểm soát kích thước không gian giải pháp.
Xác định cấu trúc tổ chức không gian giải pháp: Cấu trúc tổ chức không gian giải pháp thường được biểu diễn dưới dạng cây không gian giải pháp, dựa trên cây không gian giải pháp khác nhau, không gian giải pháp được chia thành cây con, cây hoán vị, cây m-ary, v.v.
Tìm kiếm không gian giải pháp: Theo chiến lược tìm kiếm theo chiều sâu, dựa trên ràng buộc ẩn (hàm ràng buộc và hàm giới hạn), tìm kiếm giải pháp khả thi hoặc giải pháp tốt nhất của vấn đề trong không gian giải pháp. Khi phát hiện rằng nút hiện tại không đáp ứng điều kiện giải pháp, quay lui và thử các đường khác.
- Nếu chỉ cần tìm giải pháp khả thi, chỉ cần đặt hàm ràng buộc.
- Nếu muốn tìm giải pháp tốt nhất, cần đặt hàm ràng buộc và hàm giới hạn.

Cách tiếp cận thuật toán quay lui này quá trừu tượng, không thuận tiện cho việc suy nghĩ khi làm bài tập hàng ngày. Trên thực tế, dựa trên các chương trình đệ quy, chúng ta đã tổng kết ba bước cơ bản của đệ quy. Tương tự, dựa trên ý tưởng cơ bản của thuật toán quay lui, chúng ta cũng tổng kết ba bước cơ bản của thuật toán quay lui.

Ý tưởng cơ bản của thuật toán quay lui là: Tìm kiếm giải pháp của vấn đề dựa trên chiến lược tìm kiếm theo chiều sâu, dựa trên ràng buộc của vấn đề. Khi phát hiện nút hiện tại không đáp ứng điều kiện giải pháp, quay lui và thử các đường khác.

Vì vậy, khi viết thuật toán quay lui, chúng ta có thể tuân theo ý tưởng này để viết thuật toán quay lui, các bước cụ thể như sau:

Xác định tất cả các lựa chọn: Vẽ cây quyết định tìm kiếm và dựa trên cây quyết định để xác định phạm vi tìm kiếm và các đường dẫn tương ứng.
Xác định điều kiện dừng: Xác định điều kiện dừng đệ quy, cũng như phương pháp xử lý khi đệ quy kết thúc.
Chuyển đổi cây quyết định và điều kiện dừng thành mã code:
1. Định nghĩa hàm quay lui (xác định ý nghĩa của hàm, tham số đầu vào, kết quả trả về, v.v.).
2. Viết phần thân của hàm quay lui (đưa ra ràng buộc, lựa chọn phần tử, tìm kiếm đệ quy, hủy lựa chọn, v.v.).
3. Xác định điều kiện dừng đệ quy (đưa ra điều kiện dừng đệ quy và phương pháp xử lý khi đệ quy kết thúc).

4.1 Xác định không gian giải pháp

Cây quyết định là một công cụ tốt để giúp chúng ta hiểu quy trình tìm kiếm. Chúng ta có thể vẽ cây quyết định của quy trình tìm kiếm và sử dụng cây quyết định đó để xác định phạm vi tìm kiếm và đường dẫn tìm kiếm tương ứng.

4.2 Xác định điều kiện dừng

Điều kiện dừng của thuật toán backtracking cũng chính là đáy của cây quyết định, tức là điều kiện khi không thể thực hiện thêm lựa chọn nào nữa.

Điều kiện dừng của hàm backtracking thường là độ sâu đã cho, nút lá, nút không phải lá (bao gồm cả nút gốc), tất cả các nút, v.v. Ngoài ra, cần xác định cách xử lý khi đạt đến điều kiện dừng, ví dụ như xuất kết quả, thêm kết quả thỏa mãn hiện tại vào tập hợp, v.v.

4.3 Chuyển cây quyết định và điều kiện dừng thành code

Sau khi xác định tất cả các lựa chọn và điều kiện dừng, chúng ta có thể chuyển chúng thành mã code. Bước này có thể được thực hiện theo 3 bước:

Định nghĩa hàm backtracking (xác định ý nghĩa của hàm, các tham số đầu vào và kết quả trả về).
Viết phần thân của hàm backtracking (xác định ràng buộc, lựa chọn, tìm kiếm đệ quy và hoàn tác lựa chọn).
Xác định điều kiện dừng đệ quy (xác định điều kiện dừng đệ quy và các hành động khi kết thúc đệ quy).

4.3.1 Định nghĩa hàm backtracking

Trong việc định nghĩa hàm backtracking, cần rõ ràng hiểu ý nghĩa của đệ quy, bao gồm các tham số đầu vào và biến toàn cục. Giá trị trả về của hàm nên chỉ ra vấn đề cần giải quyết.

Ví dụ, trong trường hợp hoán vị, hàm backtracking(nums) có tham số đầu vào là nums (danh sách các phần tử có thể chọn), biến toàn cục là res (mảng chứa tất cả các kết quả thỏa mãn) và path (mảng chứa kết quả thỏa mãn hiện tại). nums đại diện cho các phần tử có thể chọn hiện tại, path được sử dụng để ghi lại trạng thái hiện tại của quá trình đệ quy. res được sử dụng để lưu trữ tất cả các trạng thái của quá trình đệ quy.

4.3.2 Viết phần thân của hàm backtracking

Dựa trên danh sách các phần tử có thể chọn, ràng buộc đã cho (ví dụ như các số đã xuất hiện trước đó không thể xuất hiện lại trong các số tiếp theo cần chọn), và biến lưu trạng thái hiện tại, chúng ta có thể viết phần thân của hàm backtracking. Cụ thể là:

for i in range(len(nums)):          # Liệt kê danh sách các phần tử có thể chọn
    if Đáp ứng ràng buộc:                  # Ràng buộc
        path.append(nums[i])        # Chọn phần tử
        backtracking(nums)          # Tìm kiếm đệ quy
        path.pop()                  # Hoàn tác lựa chọn

4.3.3 Xác định điều kiện dừng đệ quy

Bước này thực chất là chuyển đổi điều kiện dừng đệ quy và các hành động tương ứng khi kết thúc đệ quy thành câu lệnh điều kiện và câu lệnh thực thi tương ứng trong mã code.

5.1 Tập con

5.1.1 Liên kết đề bài

78. Subsets

5.1.2 Tóm tắt đề bài

Mô tả: Cho một mảng số nguyên nums, các phần tử trong mảng không trùng nhau.

Yêu cầu: Trả về tất cả các tập con có thể của mảng đó. Có thể trả về kết quả theo bất kỳ thứ tự nào.

Giới hạn:

$1 \le \text{nums.length} \le 10$ .
$-10 \le \text{nums[i]} \le 10$ .
Các phần tử trong nums không trùng nhau.

Ví dụ:

Ví dụ 1:

Input: nums = [1,2,3]
Output: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

Ví dụ 2:

Input: nums = [0]
Output: [[],[0]]

5.1.3 Ý tưởng giải quyết

Ý tưởng 1: Giải thuật quay lui

Mỗi phần tử trong mảng có hai lựa chọn: chọn hoặc không chọn.

Chúng ta có thể biểu diễn việc chọn phần tử bằng cách thêm phần tử đó vào mảng con hiện tại. Hoặc sau khi kết thúc đệ quy hiện tại, chúng ta có thể loại bỏ phần tử đã thêm vào mảng con (cũng gọi là quay lui) để biểu diễn việc không chọn phần tử đó.

Dưới đây chúng ta sẽ viết giải thuật quay lui tương ứng theo ba bước của giải thuật quay lui.

Xác định tất cả các lựa chọn: Vẽ cây quyết định dựa trên việc chọn hoặc không chọn mỗi phần tử trong mảng, như hình dưới đây.
Xác định điều kiện dừng:
- Khi duyệt đến nút lá của cây quyết định, chúng ta dừng lại. Nghĩa là khi đến cuối đường dẫn hiện tại, đệ quy sẽ dừng lại.
Chuyển cây quyết định và điều kiện dừng thành Code:
1. Định nghĩa hàm quay lui:
  - backtracking(nums, index): Tham số đầu vào của hàm là nums (danh sách các phần tử có thể chọn), index (đại diện cho phần tử đang xem xét là nums[i]), biến toàn cục là res (mảng chứa tất cả các tập con thỏa mãn) và path (mảng chứa tập con hiện tại thỏa mãn).
  - Ý nghĩa của hàm backtracking(nums, index) là: Với việc chọn nums[index], đệ quy chọn các phần tử còn lại.
2. Viết phần thân của hàm quay lui (chọn phần tử, đệ quy tìm kiếm, quay lui):
  - Duyệt qua danh sách các phần tử có thể chọn từ vị trí hiện tại đến cuối mảng, và với mỗi phần tử có thể chọn:
    - Ràng buộc: Không chọn lại các phần tử đã chọn trước đó. Chúng ta bắt đầu duyệt từ vị trí index để tránh việc chọn trùng lặp. Tập con trong tập con không giống với tập con trong hoán vị. Ví dụ: {1, 2} và {2, 1} là tương đương. Để tránh việc chọn trùng lặp, chúng ta không chọn lại các phần tử đã chọn trước đó.
    - Chọn phần tử: Thêm phần tử vào mảng con hiện tại.
    - Đệ quy tìm kiếm: Với việc chọn phần tử đó, tiếp tục đệ quy xem xét các phần tử tiếp theo.
    - Quay lui: Xóa phần tử đã chọn khỏi mảng con hiện tại.
```
for i in range(index, len(nums)):   # Duyệt qua danh sách các phần tử có thể chọn
    path.append(nums[i])            # Chọn phần tử
    backtracking(nums, i + 1)       # Đệ quy tìm kiếm
    path.pop()                      # Quay lui
```
1. Xác định điều kiện dừng đệ quy (điều kiện dừng đệ quy và phương pháp xử lý khi đệ quy kết thúc):
  - Khi duyệt đến nút lá của cây quyết định, chúng ta dừng lại. Điều này có nghĩa là khi vị trí phần tử đang xem xét đạt đến cuối mảng (tức là start >= len(nums)), đệ quy dừng lại.
  - Từ cây quyết định, chúng ta cũng có thể thấy rằng tập con cần lưu trữ tất cả các nút trên cây quyết định, chúng ta cần lưu trữ tất cả các trạng thái đệ quy tìm kiếm. Vì vậy, bất kể có đạt đến điều kiện dừng hay không, chúng ta đều nên đưa kết quả thỏa mãn hiện tại vào tập hợp.

Ý tưởng 1: Code

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = []  # Mảng chứa tất cả các tập con thỏa mãn
        path = []  # Mảng chứa tập con hiện tại thỏa mãn
        def backtracking(nums, index):          # Đang xem xét phần tử thứ index trong danh sách các phần tử có thể chọn
            res.append(path[:])                 # Thêm tập con hiện tại thỏa mãn vào mảng chứa tất cả các tập con thỏa mãn
            if index >= len(nums):              # Đạt đến điều kiện dừng (trong bài này)
                return

            for i in range(index, len(nums)):   # Duyệt qua danh sách các phần tử có thể chọn
                path.append(nums[i])            # Chọn phần tử
                backtracking(nums, i + 1)       # Đệ quy tìm kiếm
                path.pop()                      # Quay lui

        backtracking(nums, 0)
        return res

Ý tưởng 1: Phân tích độ phức tạp

Độ phức tạp thời gian: $O(n \times 2^n)$ , trong đó $n$ là số lượng phần tử trong mảng nums, $2^n$ là số lượng trạng thái. Mỗi trạng thái cần $O(n)$ thời gian để xây dựng tập con.
Độ phức tạp không gian: $O(n)$ , mỗi trạng thái cần sử dụng $O(n)$ không gian để xây dựng tập con.

5.2 N-Queens

5.2.1 Liên kết đề bài

51. N-Queens

5.2.2 Tóm tắt đề bài

Mô tả: Cho một số nguyên n.

Yêu cầu: Trả về tất cả các cách sắp xếp khác nhau của vấn đề "N-Queens". Mỗi cách sắp xếp đại diện cho một cách đặt các quân hậu trên bàn cờ "N-Queens" mà không có quân hậu nào tấn công lẫn nhau.

Giới hạn:

Vấn đề N-Queens: Đặt n quân hậu lên bàn cờ n * n và đảm bảo rằng không có quân hậu nào tấn công lẫn nhau.
Quân hậu không thể tấn công nhau: Các quân hậu không thể nằm trên cùng một hàng, cột hoặc đường chéo.
$1 \le n \le 9$ .

Ví dụ:

Ví dụ 1:

Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Giải thích: Như hình dưới đây, vấn đề N-Queens có 2 cách sắp xếp khác nhau.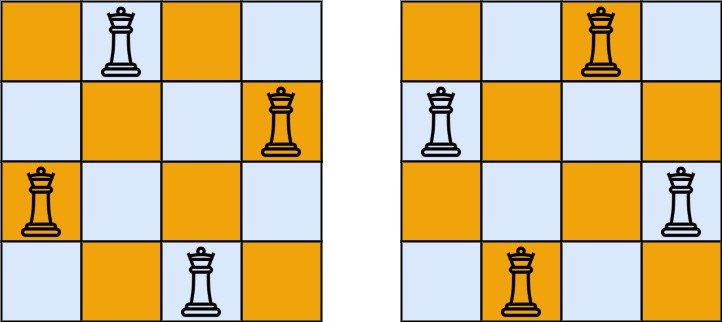

5.2.3 Ý tưởng giải quyết

Ý tưởng 1: Giải thuật quay lui

Đây là một bài toán quay lui cổ điển. Chúng ta có thể đặt các quân hậu theo thứ tự từ trên xuống dưới, từ trái sang phải.

Với bàn cờ n * n, mỗi hàng có n cột, do đó có n cách để chọn vị trí cho quân hậu trong mỗi hàng. Chúng ta có thể thử từng cột trong hàng hiện tại và kiểm tra xem nó có xung đột với các quân hậu đã đặt trước đó hay không. Nếu không có xung đột, chúng ta tiếp tục đặt quân hậu trong hàng tiếp theo. Nếu tất cả các hàng đều được đặt quân hậu mà không có xung đột, chúng ta đã tìm thấy một cách sắp xếp hợp lệ.

Sau khi đặt quân hậu, chúng ta sẽ tiếp tục đệ quy để đặt quân hậu trong hàng tiếp theo. Nếu không tìm thấy cách sắp xếp hợp lệ, chúng ta sẽ quay lại và thử các vị trí khác cho quân hậu trong hàng hiện tại.

Dưới đây chúng ta sẽ viết giải thuật quay lui tương ứng theo ba bước của giải thuật quay lui.

Xác định tất cả các lựa chọn: Vẽ cây quyết định dựa trên việc chọn hoặc không chọn mỗi vị trí cho quân hậu trong hàng, như hình dưới đây.
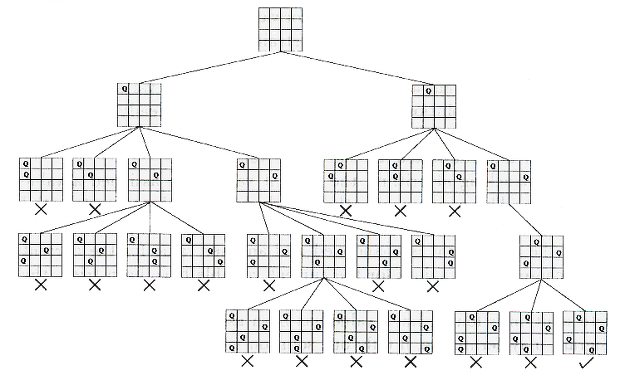
image.png
Xác định điều kiện dừng:
- Khi duyệt đến nút lá của cây quyết định, chúng ta dừng lại. Điều này có nghĩa là khi đặt quân hậu vào hàng cuối cùng (tức là row == n), đệ quy dừng lại.
Chuyển cây quyết định và điều kiện dừng thành Code:
1. Định nghĩa hàm quay lui:
  - Đầu tiên, chúng ta sử dụng một ma trận hai chiều chessboard kích thước n * n để biểu diễn bàn cờ hiện tại, trong đó ký tự Q đại diện cho quân hậu, . đại diện cho ô trống, ban đầu tất cả đều là ..
  - Sau đó, chúng ta định nghĩa hàm quay lui backtrack(chessboard, row): với tham số đầu vào là chessboard (mảng biểu diễn bàn cờ) và row (đại diện cho hàng hiện tại đang xem xét), biến toàn cục là res (mảng chứa tất cả các cách sắp xếp hợp lệ).
  - Ý nghĩa của hàm backtrack(chessboard, row) là: Với việc đặt quân hậu vào hàng row đã cho, tiếp tục đệ quy để đặt quân hậu trong các hàng còn lại.
2. Viết phần thân của hàm quay lui (chọn vị trí, đệ quy tìm kiếm, quay lui):
  - Duyệt qua tất cả các cột trong hàng hiện tại. Với mỗi vị trí cột:
    - Ràng buộc: Định nghĩa một phương thức kiểm tra, trước tiên kiểm tra xem vị trí hiện tại có xung đột với các quân hậu đã đặt trước đó không. Nếu không có xung đột, tiếp tục đặt quân hậu trong hàng tiếp theo. Nếu có xung đột, tiếp tục duyệt qua các vị trí cột khác.
    - Chọn vị trí: Đặt quân hậu vào vị trí row, col, đặt giá trị tương ứng trong mảng chessboard thành Q.
    - Đệ quy tìm kiếm: Với việc đặt quân hậu tại vị trí đó, tiếp tục đệ quy để đặt quân hậu trong các hàng tiếp theo.
    - Quay lui: Đặt giá trị tại vị trí row, col trong mảng chessboard thành ..
```
# Kiểm tra xem vị trí row, col có xung đột với các quân hậu đã đặt trước đó không
def isValid(self, n: int, row: int, col: int, chessboard: List[List[str]]):
    # Kiểm tra xung động cột
    for i in range(row):
        if chessboard[i][col] == 'Q':
            return False
    # Kiểm tra xung đột đường chéo chính
    i, j = row - 1, col - 1
    while i >= 0 and j >= 0:
        if chessboard[i][j] == 'Q':
            return False
        i -= 1
        j -= 1
    # Kiểm tra xung dột đường chéo phụ
    i, j = row - 1, col + 1
    while i >= 0 and j < n:
        if chessboard[i][j] == 'Q':
            return False
        i -= 1
        j += 1

    return True
```
```
for col in range(n):                            # Duyệt qua tất cả các cột trong hàng hiện tại
    if self.isValid(n, row, col, chessboard):   # Nếu vị trí hiện tại không xung đột với các quân hậu đã đặt trước đó
        chessboard[row][col] = 'Q'              # Đặt quân hậu vào vị trí row, col
        backtrack(row + 1, chessboard)          # Đệ quy để đặt quân hậu trong các hàng tiếp theo
        chessboard[row][col] = '.'              # Quay lui: Đặt giá trị tại vị trí row, col thành '.'
```
1. Xác định điều kiện dừng đệ quy (điều kiện dừng đệ quy và phương pháp xử lý khi đệ quy kết thúc):
  - Khi duyệt đến nút lá của cây quyết định, chúng ta dừng lại. Điều này có nghĩa là khi đặt quân hậu vào hàng cuối cùng (tức là row == n), đệ quy dừng lại.
  - Khi đệ quy dừng lại, chúng ta sẽ chuyển đổi bàn cờ hiện tại thành định dạng yêu cầu và lưu nó vào mảng kết quả res.

Ý tưởng 1: Code

class Solution:
    res = []
    def backtrack(self, n: int, row: int, chessboard: List[List[str]]):
        if row == n:
            temp_res = []
            for temp in chessboard:
                temp_str = ''.join(temp)
                temp_res.append(temp_str)
            self.res.append(temp_res)
            return
        for col in range(n):
            if self.isValid(n, row, col, chessboard):
                chessboard[row][col] = 'Q'
                self.backtrack(n, row + 1, chessboard)
                chessboard[row][col] = '.'

    def isValid(self, n: int, row: int, col: int, chessboard: List[List[str]]):
        for i in range(row):
            if chessboard[i][col] == 'Q':
                return False

        i, j = row - 1, col - 1
        while i >= 0 and j >= 0:
            if chessboard[i][j] == 'Q':
                return False
            i -= 1
            j -= 1
        i, j = row - 1, col + 1
        while i >= 0 and j < n:
            if chessboard[i][j] == 'Q':
                return False
            i -= 1
            j += 1

        return True

    def solveNQueens(self, n: int) -> List[List[str]]:
        self.res.clear()
        chessboard = [['.' for _ in range(n)] for _ in range(n)]
        self.backtrack(n, 0, chessboard)
        return self.res

Ý tưởng 1: Phân tích độ phức tạp

Độ phức tạp thời gian: $O(n!)$ , trong đó $n$ là số lượng quân hậu.
Độ phức tạp không gian: $O(n^2)$ , trong đó $n$ là số lượng quân hậu. Số lượng lời gọi đệ quy không vượt quá $n$ , mỗi bảng cờ có độ phức tạp không gian là $O(n^2)$ , do đó độ phức tạp không gian là $O(n^2)$ .

Ý tưởng 1: Cải tiến

Tôi đang viết ý tưởng theo khung giải quyết bài toán quay lui để các bạn có thể dễ hiểu hơn. Khi nào bạn đã quen với lối suy nghĩ bạn có thể linh hoạt hơn trong việc code, không phải rập khuôn như thế này!

Nếu bạn suy luận thêm thì ta có thể cải tiến phần kiểm tra xung đột bằng phương pháp đánh dấu. Tức là với một ô $(i, j)$ thì xem thử cột $j$ và hai đường chéo đi qua nó đã có quân hậu nào chưa. Đối với 2 đường chéo, chúng có đặc điểm sau:

Với tất cả các ô $(i, j)$ $(i, j)$ nằm trên cùng:
- Chéo chính: hiêu $i - j$ là như nhau
- Chéo phụ: tổng $i + j$ là như nhau

Từ đó ta có thể áp dụng phương pháp đánh dấu bằng cách sử dụng mảng hoặc set. Bạn có thể tự xử lý xem như một bài tập nhỏ.