Minimum Spanning Tree
1. Giới thiệu cây khung nhỏ nhất
Hãy bắt đầu bằng việc nói về sự khác biệt cơ bản giữa "cây" và "đồ thị": Cây không chứa chu trình, trong khi đồ thị có thể chứa chu trình.
Nếu một đồ thị không có chu trình, nó hoàn toàn có thể được kéo dài thành dạng cây. Nói một cách chuyên nghiệp, cây là "đồ thị liên thông không có chu trình".
Vậy "cây khung" trong đồ thị là gì? Thực ra, nó dễ hiểu theo nghĩa đen, đó là tìm một cây con liên thông chứa tất cả các đỉnh trong đồ thị. Chuyên nghiệp hơn, cây khung (spanning tree) là một "đồ thị con liên thông không có chu trình" chứa tất cả các đỉnh trong đồ thị.
Dễ hiểu rằng, một đồ thị có thể có nhiều cây khung khác nhau, ví dụ như đồ thị dưới đây, các cạnh màu đỏ tạo thành hai cây khung khác nhau:
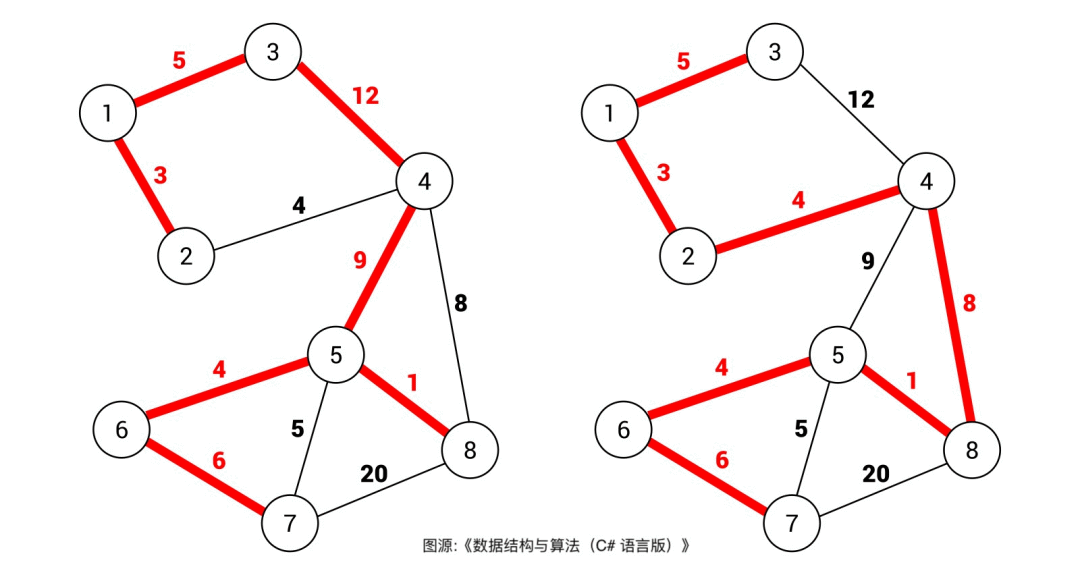
Đối với đồ thị có trọng số, mỗi cạnh đều có trọng số, vì vậy mỗi cây khung cũng có một tổng trọng số. Ví dụ trên, tổng trọng số của cây khung bên phải rõ ràng nhỏ hơn tổng trọng số của cây khung bên trái.
Vậy cây khung nhỏ nhất rất dễ hiểu, trong tất cả các cây khung có thể có, cây khung có tổng trọng số nhỏ nhất được gọi là "cây khung nhỏ nhất (minimum spanning tree)". Tương tự đói với cây khung lớn nhất!
PS: Thông thường, chúng ta thường tính toán cây khung nhỏ nhất trên đồ thị vô hướng có trọng số, vì vậy trong các tình huống thực tế sử dụng thuật toán cây khung nhỏ nhất, trọng số cạnh của đồ thị thường đại diện cho chi phí, khoảng cách hoặc các giá trị tương tự.
2. Các tính chất của cây khung nhỏ nhất
Dưới đây là một vài tính chất của cây khung nhỏ nhất trong đồ thị vô hướng có trọng số:
Warning
Các bạn đọc mới học chỉ cần đọc và nhớ các tính chất, chưa cần chứng minh. Các tính chất này hoàn toàn có thể chứng minh bằng phản chứng nhưng sẽ khá là hàn lâm. Bạn có thể xem phần chứng minh ở Bài toán tìm cây khung nhỏ nhất trong đồ thị
2.1 Đường đi hẹp nhất
Gọi độ rộng của một đường đi trên đồ thị là trọng số lớn nhất trong các trọng số của cách cạnh trên đường đi đó. Khi đó ta có: đường đi giữa 2 đỉnh và trên cây khung nhỏ nhất chính là đường đi hẹp nhất giữa 2 đỉnh đó.
Rõ ràng hơn: Với 2 đỉnh và trong đồ thị, nếu là trọng số cạnh lớn nhất trên đường đi từ đến trên cây khung nhỏ nhất thì ta không thể tìm được đường đi nào khác từ tới mà mà chỉ đi qua những cạnh có trọng số nhỏ hơn .
Mở rộng hơn, ta có đường đi trên cây khung nhỏ nhất chính là đường đi có cạnh lớn nhất là nhỏ nhất, còn đường đi trên cây khung lớn nhất có cạnh nhỏ nhất là lớn nhất.
Cần chú ý tính chất này vì nó được sử dụng trong nhiều bài tập.
2.2 Tính duy nhất
Nếu tất cả các cạnh đều có trọng số khác nhau thì chỉ có duy một cây khung nhỏ nhất. Ngược lại, nếu một vài cạnh có trọng số giống nhau thì có thể có nhiều hơn một cây khung nhỏ nhất.
2.3 Tính chất chu trình
Trong một chu trình bất kì, nếu cạnh có trọng số lớn hơn tất cả các cạnh còn lại thì không thể nằm trong cây khung nhỏ nhất.
2.4 Tính chất cắt
Xét một lát cắt bất kì, gọi là tập hợp các cạnh trong lát cắt đó (các cạnh bị loại bỏ để đồ thị bị chia làm 2 thành phần liên thông). Nếu là cạnh trong và có trọng số nhỏ hơn tất cả các cạnh khác của thì nằm trong cây khung nhỏ nhất của đồ thị.
2.5 Tính chất cạnh nhỏ nhất
Nếu là cạnh có trọng số nhỏ nhất của đồ thị, và không có cạnh nào có trọng số bằng thì nằm trong mọi cây khung nhỏ nhất của đồ thị.
3. Thuật toán tìm kiếm cây khung nhỏ nhất
Có 2 thuật toán tìm cây khung nhỏ nhất nổi tiếng:
- [[Kruskal]]
- [[Prim]]
Ở bài viết này tôi chỉ giới thiệu sơ qua, vì nếu viết sẽ quá dài nên bạn hãy truy cập vào từng bài viết để đọc cụ thể.
3.1 Kruskal
Thuật toán Kruskal xây dựng cây khung nhỏ nhất bằng cách duyệt các cạnh theo trọng số từ nhỏ tới lớn và hợp nhất dần các đỉnh vào các vùng cho tới khi chỉ còn lại một vùng duy nhất. Với mỗi cạnh sẽ xem xét 2 đỉnh đã cùng một vùng chưa, nếu không sẽ hợp nhất 2 vùng của 2 đỉnh, cấu trúc [[Disjoint Set Union]] được sử dụng để làm điều này. Vì việc sắp xếp cạnh tăng dần theo trọng số nên đảm bảo cây khung sẽ nhỏ nhất!
Chi tiết về thuật toán vui lòng xem: [[Kruskal]]
3.2 Prim
Thuật toán Prim xây dựng cây khung nhỏ nhất bắt đầu từ một đỉnh và sẽ tìm nạp các đỉnh tiếp theo gần cây nhất vào cây. Gần cây nhất ở đây là khoảng cách của đỉnh đó tới một đỉnh đã ở trong cây là ngắn nhất, cấu trúc hàng đợi ưu tiên ([[Priority Queue]]) được sủ dụng để tìm ra đỉnh gần nhất này. Điều này sẽ đảm bảo cây khung là nhỏ nhất.
Nếu bạn đã tìm hiểu thuật toán [[Dijkstra]], bạn sẽ hiểu ngay và luôn thuật toán [[Prim]] vì tư tưởng và cách cài đặt của chúng cực kì giống nhau!
Chi tiết về thuật toán vui lòng xem: [[Prim]]