Tree DP

1. Giới thiệu về Quy hoạch động trên cây

Quy hoạch động trên cây: Thường được gọi là "DP trên cây", là một phương pháp quy hoạch động được áp dụng trên cấu trúc cây. Như hình dưới đây, quá trình giải quyết vấn đề DP trên cây thường được thực hiện theo thứ tự từ độ sâu của các nút (từ cây con nhỏ đến lớn) làm "giai đoạn" của quy hoạch động. Trong DP trên cây, chiều thứ nhất thường là số hiệu của nút, đại diện cho cây con có gốc tại nút đó.

Có nhiều cách để chia nhỏ vấn đề của DP trên cây.

Nếu chia nhỏ theo "hướng chuyển tiếp của giai đoạn", có thể chia thành hai loại sau:

1. Từ dưới lên: Tính toán từng cây con bằng cách đệ quy, sau đó trong quá trình quay lui, chuyển đổi trạng thái từ các nút con lên nút cha. Chỉ khi tất cả các cây con của nút hiện tại đã được tính toán, chúng ta mới có thể tính toán nút hiện tại và tiếp tục tính toán từ trên xuống.
2. Từ trên xuống: Bắt đầu từ nút gốc, tính toán trạng thái của các nút con từ trên xuống. Phương pháp này thường sử dụng tìm kiếm theo bộ nhớ để tránh tính toán trùng lặp và tăng hiệu suất.

Vấn đề DP trên cây theo hướng "từ trên xuống" khá hiếm gặp, hầu hết các vấn đề DP trên cây đều sử dụng hướng "từ dưới lên" để giải quyết.

Nếu chia nhỏ theo "có cố định gốc hay không", có thể chia thành hai loại sau:

1. DP trên cây có gốc cố định: Vấn đề DP trên cây có gốc được xác định trước, thường chỉ cần bắt đầu từ nút gốc đã cho và sử dụng một lần tìm kiếm theo chiều sâu.
2. DP trên cây không có gốc cố định: Vấn đề DP trên cây không có gốc được xác định trước và thay đổi gốc có thể ảnh hưởng đến một số giá trị như tổng độ sâu của các nút con, tổng trọng số của các nút, v.v. Thường cần sử dụng hai lần tìm kiếm theo chiều sâu, lần thứ nhất để tiền xử lý thông tin như độ sâu, tổng trọng số của các nút, và lần thứ hai để chạy DP trên cây với gốc thay đổi.

Trong bài viết này, chúng tôi sẽ phân loại các vấn đề DP trên cây thành hai loại dựa trên "có cố định gốc hay không" và giải thích từng loại vấn đề này.

2. Quy hoạch động trên cây có gốc cố định

2.1 Ý tưởng chung của quy hoạch động trên cây có gốc cố định

Với các bài toán quy hoạch động trên cây có gốc cố định, nếu cây là một cây nhị phân, thì thông thường cây được đưa ra dưới dạng một nút gốc. Chúng ta có thể bắt đầu tìm kiếm theo chiều sâu từ nút gốc đã cho. Nếu cây là một cây đa phân, thì cây được đưa ra dưới dạng một đồ thị vô hướng với $n$ nút và $n-1$ cạnh, và nút gốc đã được chỉ định trước. Trong trường hợp này, chúng ta cần lưu trữ các đỉnh và cạnh trong danh sách kề và bắt đầu tìm kiếm theo chiều sâu từ nút gốc đã cho. Trong quá trình duyệt, chúng ta cần đánh dấu các nút đã được truy cập để tránh quay lại nút cha theo cạnh ngược.

Dưới đây là hai ví dụ để giải thích ý tưởng chung của quy hoạch động trên cây.

2.2 Tìm đường đi dài nhất trong cây

2.2.1 Liên kết đến bài toán

• 124. Binary Tree Maximum Path Sum

2.2.2 Đề bài

Mô tả: Cho một nút gốc của một cây nhị phân.

Yêu cầu: Hãy trả về tổng lớn nhất của đường đi trong cây.

Giải thích:

• Đường đi: Được xác định là một chuỗi các nút, trong đó mỗi cặp nút liền kề được nối bởi một cạnh. Mỗi nút chỉ xuất hiện một lần trong đường đi. Đường đi có ít nhất một nút và không nhất thiết phải đi qua nút gốc.
• Tổng đường đi: Tổng của các giá trị của các nút trong đường đi.
• Số lượng nút trong cây nằm trong khoảng từ $1$ đến $3 \times 10^4$.
• Giá trị của mỗi nút nằm trong khoảng từ $-1000$ đến $1000$.

Ví dụ:

• Ví dụ 1:

Input: root = [1,2,3]
Output: 6
Explanation: Đường đi tối ưu là 2 -> 1 -> 3, tổng là 2 + 1 + 3 = 6.

• Ví dụ 2:

Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: Đường đi tối ưu là 15 -> 20 -> 7, tổng là 15 + 20 + 7 = 42.

2.2.3 Ý tưởng giải quyết

Ý tưởng 1: Quy hoạch động trên cây + Tìm kiếm theo chiều sâu

Dựa trên việc đường đi tối ưu có đi qua nút gốc hay không, chúng ta có thể chia cây nhị phân thành hai trường hợp:

1. Đường đi tối ưu đi qua nút gốc.
2. Đường đi tối ưu không đi qua nút gốc.

Nếu đường đi tối ưu đi qua nút gốc, thì: Đường đi lớn nhất trong cây = Đường đi lớn nhất từ cây con bên trái + Đường đi lớn nhất từ cây con bên phải + Giá trị của nút hiện tại.

Nếu đường đi tối ưu không đi qua nút gốc, thì: Đường đi lớn nhất trong cây = Đường đi lớn nhất trong tất cả các cây con.

Chúng ta có thể sử dụng tìm kiếm theo chiều sâu đệ quy để duyệt qua cây nhị phân và trong quá trình duyệt, chúng ta duy trì một biến tổng đường đi lớn nhất $ans$.

Sau đó, chúng ta định nghĩa hàm def dfs(self, node): để tính toán đường đi lớn nhất trong cây có gốc tại nút đó.

Có hai trường hợp kết quả có thể xảy ra:

1. Đường đi lớn nhất khi đi qua nút rỗng bằng $0$.
2. Đường đi lớn nhất khi đi qua nút không rỗng bằng Giá trị hiện tại của nút + đường đi lớn nhất từ cây con bên trái hoặc cây con bên phải. Nếu đường đi lớn nhất là số âm, chúng ta có thể xem xét bỏ qua nó, tức là đường đi lớn nhất bằng $0$.

Trong quá trình đệ quy, chúng ta tính toán đường đi lớn nhất từ cây con bên trái và cây con bên phải trước, sau đó cập nhật và duy trì biến tổng đường đi lớn nhất $ans$. Cuối cùng, $ans$ sẽ là kết quả. Các bước cụ thể như sau:

1. Nếu nút gốc $root$ là rỗng, trả về $0$.
2. Tính toán đường đi lớn nhất từ cây con bên trái và gán cho $left\underline{}max$.
3. Tính toán đường đi lớn nhất từ cây con bên phải và gán cho $right\underline{}max$.
4. Cập nhật và duy trì biến tổng đường đi lớn nhất $ans$, tức là $self.ans = max \lbrace self.ans, \quad left\underline{}max + right\underline{}max + node.val \rbrace$.
5. Trả về đường đi lớn nhất từ cây có gốc tại nút hiện tại, tức là $max(left\underline{}max, right\underline{}max) + node.val$.
6. Cuối cùng, trả về $self.ans$ là kết quả.

Ý tưởng 1: Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def __init__(self):
        self.ans = float('-inf')
        
    def dfs(self, node):
        if not node:
            return 0
        left_max = max(self.dfs(node.left), 0)     # đường đi lớn nhất từ cây con bên trái
        right_max = max(self.dfs(node.right), 0)   # đường đi lớn nhất từ cây con bên phải

        cur_max = left_max + right_max + node.val  # Tổng đường đi lớn nhất chứa nút hiện tại và cây con bên trái, bên phải
        self.ans = max(self.ans, cur_max)          # Cập nhật tổng đường đi lớn nhất trong cây

        return max(left_max, right_max) + node.val # Trả về đường đi lớn nhất từ cây có gốc tại nút hiện tại

    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        self.dfs(root)
        return self.ans

Ý tưởng 1: Phân tích độ phức tạp

• Độ phức tạp thời gian: $O(n)$, trong đó $n$ là số lượng nút trong cây nhị phân.
• Độ phức tạp không gian: $O(n)$. Hàm đệ quy cần sử dụng không gian trong ngăn xếp, không gian trong ngăn xếp phụ thuộc vào độ sâu của đệ quy, trong trường hợp xấu nhất, độ sâu đệ quy là $n$, do đó không gian là $O(n)$.

2.3 Đường đi dài nhất với các ký tự kề nhau khác nhau

2.3.1 Liên kết đến bài toán

• 2246. Longest Path With Different Adjacent Characters

2.3.2 Đề bài

Mô tả: Cho một mảng $parent$ có độ dài $n$ để biểu diễn một cây (tức là một đồ thị liên thông, vô hướng và không có chu trình). Cây có $n$ đỉnh, trong đó đỉnh gốc có chỉ số là $0$. Trong đó, $parent[i]$ biểu diễn đỉnh cha của đỉnh $i$. Vì đỉnh gốc có chỉ số là $0$, nên $parent[0] = -1$. Cho một chuỗi có độ dài $n$, trong đó $s[i]$ biểu diễn ký tự được gán cho đỉnh $i$.

Yêu cầu: Tìm đường đi dài nhất trong cây sao cho không có cặp đỉnh kề nhau có cùng ký tự, và trả về độ dài của đường đi đó.

Giải thích:

• $n = parent.length = s.length$.
• $1 \le n \le 10^5$.
• Với mọi $i \ge 1$, $0 \le parent[i] \le n - 1$.
• $parent[0] = -1$.
• $parent$ biểu diễn một cây hợp lệ.
• $s$ chỉ bao gồm các ký tự chữ cái thường.

Ví dụ:

• Ví dụ 1:

Input: parent = [-1,0,0,1,1,2], s = "abacbe"
Output: 3
Explanation: Đường đi dài nhất trong cây sao cho không có cặp đỉnh kề nhau có cùng ký tự là: 0 -> 1 -> 3. Độ dài của đường đi này là 3, nên trả về 3.
Có thể chứng minh rằng không tồn tại đường đi khác thoả mãn yêu cầu và có độ dài lớn hơn 3.

• Ví dụ 2:

Input: parent = [-1,0,0,0], s = "aabc"
Output: 3
Explanation: Đường đi dài nhất trong cây sao cho không có cặp đỉnh kề nhau có cùng ký tự là: 2 -> 0 -> 3. Độ dài của đường đi này là 3, nên trả về 3.

2.3.3 Ý tưởng giải quyết

Ý tưởng 1: Quy hoạch động trên cây + Tìm kiếm theo chiều sâu

Vì đề bài đã cho mảng $parent$ biểu diễn quan hệ cha con, để thuận tiện cho việc duyệt các đỉnh kề nhau, chúng ta có thể xây dựng một đồ thị có hướng $graph$ từ mảng $parent$, trong đó mỗi đỉnh cha chỉ đến các đỉnh con.

Nếu không xét đến điều kiện các đỉnh kề nhau có cùng ký tự, thì bài toán này tương đương với việc tìm đường kính của cây (độ dài đường đi dài nhất trong cây).

Đối với cây có gốc tại đỉnh $u$:

1. Nếu đường đi dài nhất đi qua đỉnh gốc $u$, thì: Độ dài đường đi dài nhất = Độ dài đường đi dài nhất trong một cây con + Độ dài đường đi dài nhất trong cây con còn lại + 1.
2. Nếu đường đi dài nhất không đi qua đỉnh gốc $u$, thì: Độ dài đường đi dài nhất = Độ dài đường đi dài nhất trong một cây con.

Tức là: Độ dài đường đi dài nhất = max(Độ dài đường đi dài nhất trong một cây con + Độ dài đường đi dài nhất trong cây con còn lại + 1, Độ dài đường đi dài nhất trong một cây con).

Chúng ta có thể sử dụng tìm kiếm theo chiều sâu để duyệt qua các đỉnh kề nhau của $u$, và trong quá trình duyệt, chúng ta duy trì một biến $ans$ để lưu trữ độ dài đường đi dài nhất toàn cầu, và biến $u\underline{}len$ để lưu trữ độ dài đường đi dài nhất của đỉnh $u$ hiện tại.

1. Đầu tiên, tính toán độ dài đường đi dài nhất $v\underline{}len$ từ một đỉnh con $v$.
2. Cập nhật giá trị $ans$ bằng cách so sánh $u\underline{}len + v\underline{}len + 1$ với $ans$.
3. Cập nhật giá trị $u\underline{}len$ bằng cách so sánh $u\underline{}len$ với $v\underline{}len + 1$.

Vì đề bài yêu cầu "các đỉnh kề nhau không được có cùng ký tự", nên khi cập nhật giá trị $ans$ và $u\underline{}len$, chúng ta cần kiểm tra xem đỉnh $u$ và đỉnh $v$ có cùng ký tự hay không, chỉ khi hai đỉnh có ký tự khác nhau, chúng ta mới có thể cập nhật giá trị.

Cuối cùng, vì đề bài yêu cầu tìm đường kính của cây (độ dài đường đi dài nhất trong cây), và: Số đỉnh trên đường đi = Độ dài đường đi + 1, nên chúng ta trả về $ans + 1$ là kết quả.

Ý tưởng 1: Code

class Solution:
    def longestPath(self, parent: List[int], s: str) -> int:
        size = len(parent)

        # Xây dựng đồ thị từ mảng parent
        graph = [[] for _ in range(size)]
        for i in range(1, size):
            graph[parent[i]].append(i)

        ans = 0
        def dfs(u):
            nonlocal ans
            u_len = 0                                   # Độ dài đường đi dài nhất của đỉnh u
            for v in graph[u]:                          # Duyệt qua các đỉnh kề nhau của u
                v_len = dfs(v)                          # Độ dài đường đi dài nhất của đỉnh v
                if s[u] != s[v]:                        # Kiểm tra hai đỉnh có ký tự khác nhau hay không
                    ans = max(ans, u_len + v_len + 1)   # Cập nhật độ dài đường đi dài nhất toàn cầu
                    u_len = max(u_len, v_len + 1)       # Cập nhật độ dài đường đi dài nhất của đỉnh u
            return u_len                                # Trả về độ dài đường đi dài nhất của đỉnh u

        dfs(0)
        return ans + 1

Ý tưởng 1: Phân tích độ phức tạp

• Độ phức tạp thời gian: $O(n)$, trong đó $n$ là số lượng đỉnh trong cây.
• Độ phức tạp không gian: $O(n)$.

3. Quy hoạch động trên cây không có gốc cố định

3.1 Ý tưởng chung của quy hoạch động trên cây không có gốc cố định

Với các bài toán quy hoạch động trên cây không có gốc cố định, nếu cây là một cây nhị phân, thì cây được đưa ra dưới dạng một đồ thị vô hướng với $n$ đỉnh và $n-1$ cạnh, và không có đỉnh gốc được chỉ định trước. Trong trường hợp này, chúng ta cần lưu trữ các đỉnh và cạnh trong danh sách kề và bắt đầu tìm kiếm theo chiều sâu từ một đỉnh bất kỳ.

Dưới đây là hai ví dụ để giải thích ý tưởng chung của quy hoạch động trên cây.

3.2 Tìm cây có chiều cao nhỏ nhất

3.2.1 Đường dẫn đến đề bài

• 310. Minimum Height Trees

3.2.2 Tóm tắt đề bài

Mô tả: Có một cây có $n$ đỉnh, các đỉnh được đánh số từ $0$ đến $n - 1$. Cho một số nguyên $n$ và một danh sách $edges$ gồm $n - 1$ cạnh vô hướng để biểu diễn cây này. Trong đó, $edges[i] = [ai, bi]$ biểu thị sự tồn tại của một cạnh vô hướng giữa đỉnh $ai$ và $bi$.

Có thể chọn bất kỳ đỉnh nào trong cây làm gốc. Khi chọn đỉnh $x$ làm gốc, chiều cao của cây kết quả được ký hiệu là $h$. Trong tất cả các cây có thể, cây có chiều cao nhỏ nhất (tức $min(h)$) được gọi là cây có chiều cao nhỏ nhất.

Yêu cầu: Tìm tất cả các cây có chiều cao nhỏ nhất và trả về danh sách các đỉnh gốc của chúng theo bất kỳ thứ tự nào.

Giải thích:

• Chiều cao của cây: Là số cạnh trên đường đi dài nhất từ gốc đến lá.
• $1 \le n \le 2 * 10^4$.
• $edges.length == n - 1$.
• $0 \le ai, bi < n$.
• $ai \ne bi$.
• Tất cả các cặp $(ai, bi)$ đều khác nhau.
• Đầu vào được đảm bảo là một cây và không có cạnh trùng lặp.

Ví dụ:

• Ví dụ 1:

Input: n = 4, edges = [[1,0],[1,2],[1,3]]
Output: [1]
Explanation: Khi chọn đỉnh có nhãn là 1 làm gốc, chiều cao của cây là 1, đây là cây có chiều cao nhỏ nhất duy nhất.

• Ví dụ 2:

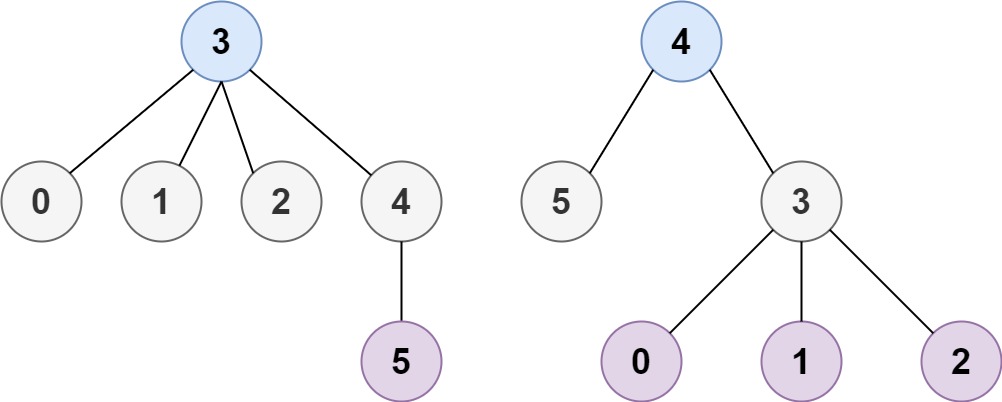
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Output: [3,4]

Ý tưởng 1: Duyệt cây + Phương pháp thay đổi gốc cây

Phương pháp đầu tiên dễ nhất để giải quyết bài toán này là duyệt qua $n$ đỉnh, chọn mỗi đỉnh làm gốc cây và thực hiện tìm kiếm theo chiều sâu để tính toán chiều cao của mỗi cây. Cuối cùng, tìm cây có chiều cao nhỏ nhất trong tất cả các cây và trả về danh sách các đỉnh gốc của chúng. Tuy nhiên, phương pháp này có độ phức tạp thời gian là $O(n^2)$, trong khi $n$ nằm trong khoảng từ $1$ đến $2 \times 10^4$. Do đó, cần tối ưu hóa phương pháp này.

Trong phương pháp trên, trong quá trình tìm kiếm theo chiều sâu, ngoài việc tính toán chiều cao của cây, chúng ta cũng có thể tính toán chiều cao của cây khi chọn mỗi đỉnh con làm gốc cây. Nếu chúng ta có thể sử dụng thông tin về chiều cao của các cây con này để nhanh chóng tính toán chiều cao của cây khi chọn các đỉnh khác làm gốc cây, thì chúng ta có thể cải thiện phương pháp và giảm độ phức tạp thời gian.

Để làm được điều này, chúng ta sẽ sử dụng phương pháp thay đổi gốc cây. Ý tưởng chính là:

1. Lần duyệt đầu tiên: Tính toán độ dài đường đi dài nhất và đường đi thứ hai dài nhất từ mỗi nút xuống (được lưu trữ trong mảng down1 và down2) và ghi lại nút con mà đường đi dài nhất đi qua (được lưu trữ trong mảng p).
2. Lần duyệt thứ hai: Tính toán độ dài đường đi dài nhất từ mỗi nút lên (được lưu trữ trong mảng up). Khi tính toán up[v], chúng ta sẽ kiểm tra xem đường đi dài nhất từ nút cha của v có đi qua nút v không. Nếu có, độ dài đường đi dài nhất từ nút cha của v lên là max(up[u], down2[u]) + 1, ngược lại, độ dài đường đi dài nhất từ nút cha của v lên là max(up[u], down1[u]) + 1.
3. Tìm cây có chiều cao nhỏ nhất trong tất cả các cây và trả về danh sách các đỉnh gốc của chúng.

Ý tưởng 1: Code

class Solution:
    def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
        graph = [[] for _ in range(n)]
        for u, v in edges:
            graph[u].append(v)
            graph[v].append(u)
		
        # down1 dùng để lưu trữ đường đi dài nhất xuống
        down1 = [0 for _ in range(n)]
        # down2 dùng để lưu trữ đường đi thứ hai dài nhất xuống
        down2 = [0 for _ in range(n)]
        p = [0 for _ in range(n)]
        # Duyệt từ dưới lên để tính toán thông tin
        def dfs(u, fa):
            for v in graph[u]:
                if v == fa:
                    continue
                # Duyệt từ dưới lên để tính toán thông tin
                dfs(v, u)                   
                height = down1[v] + 1
                if height >= down1[u]:
                    down2[u] = down1[u]
                    down1[u] = height
                    p[u] = v
                elif height > down2[u]:
                    down2[u] = height

        # Duyệt từ trên xuống để tính toán thông tin
        up = [0 for _ in range(n)]
        def reroot(u, fa):
            for v in graph[u]:
                if v == fa:
                    continue
                if p[u] == v:
                    up[v] = max(up[u], down2[u]) + 1
                else:
                    up[v] = max(up[u], down1[u]) + 1
                # Duyệt từ trên xuống để tính toán thông tin
                reroot(v, u)                            

        dfs(0, -1)
        reroot(0, -1)

        # Tìm cây có chiều cao nhỏ nhất trong tất cả các cây
        min_h = 1e9
        for i in range(n):
            min_h = min(min_h, max(down1[i], up[i]))

        # Trả về danh sách các đỉnh gốc của cây có chiều cao nhỏ nhất
        res = []
        for i in range(n):
            if max(down1[i], up[i]) == min_h:
                res.append(i)

        return res

Ý tưởng 1: Phân tích độ phức tạp

• Độ phức tạp thời gian: $O(n)$.
• Độ phức tạp không gian: $O(n)$.