Skip to main content

Interval DP

Hung NguyenAbout 13 mindsaalgorithmdsaalgorithm

1. Giới thiệu về Quy hoạch động trên đoạn

1.1 Định nghĩa Quy hoạch động trên đoạn

Quy hoạch động trên đoạn: Là một dạng của Quy hoạch động tuyến tính, thường được gọi là "Quy hoạch động trên đoạn". Nó chia các giai đoạn dựa trên "độ dài đoạn" và sử dụng hai chỉ số (điểm bắt đầu và điểm kết thúc của đoạn) làm chiều của trạng thái. Một trạng thái thường được chuyển từ các trạng thái nhỏ hơn nó và nhỏ hơn nó.

Ý tưởng chính của Quy hoạch động trên đoạn là: trước tiên tìm giải pháp tối ưu trong các đoạn nhỏ, sau đó kết hợp các giải pháp tối ưu trong các đoạn nhỏ này để có được giải pháp tối ưu cho đoạn lớn hơn, cuối cùng là giải pháp tối ưu cho toàn bộ đoạn.

Dựa trên cách chuyển đổi từ các đoạn nhỏ sang đoạn lớn khác nhau, các bài toán Quy hoạch động trên đoạn thường được chia thành hai loại:

  1. Các bài toán Quy hoạch động trên đoạn chuyển từ giữa sang hai phía. Ví dụ: chuyển từ đoạn [i+1,j−1][i + 1, j - 1] sang đoạn lớn hơn [i,j][i, j].
  2. Các bài toán Quy hoạch động trên đoạn chuyển từ nhiều đoạn nhỏ (từ 2 đoạn trở lên) sang đoạn lớn hơn. Ví dụ: chuyển từ đoạn [i,k][i, k] và đoạn [k,j][k, j] sang đoạn [i,j][i, j].

Dưới đây, chúng ta sẽ trình bày cách tiếp cận cơ bản cho hai loại bài toán Quy hoạch động trên đoạn này.

1.2 Cách tiếp cận cơ bản cho bài toán Quy hoạch động trên đoạn

1.2.1 Cách tiếp cận cơ bản cho loại bài toán thứ nhất

Cách tiếp cận cơ bản cho bài toán Quy hoạch động trên đoạn chuyển từ giữa sang hai phía là sử dụng công thức chuyển trạng thái sau: dp[i][j]=max{dp[i+1][j−1],dp[i+1][j],dp[i][j−1]}+cost[i][j],i≤jdp[i][j] = max \lbrace dp[i + 1][j - 1], \quad dp[i + 1][j], \quad dp[i][j - 1] \rbrace + cost[i][j], \quad i \le j.

  1. Trong đó dp[i][j]dp[i][j] biểu thị giá trị lớn nhất trên đoạn [i,j][i, j] (tức là tất cả các phần tử từ vị trí ii đến vị trí jj).
  2. costcost biểu thị chi phí để chuyển từ đoạn nhỏ sang đoạn [i,j][i, j].
  3. max/minmax / min ở đây phụ thuộc vào việc bài toán yêu cầu tìm giá trị lớn nhất hay nhỏ nhất.

Cách tiếp cận cơ bản cho bài toán Quy hoạch động trên đoạn chuyển từ giữa sang hai phía như sau:

  1. Duyệt qua các điểm bắt đầu của đoạn.
  2. Duyệt qua các điểm kết thúc của đoạn.
  3. Tính toán giá trị tối ưu sau khi chuyển từ đoạn nhỏ sang đoạn lớn bằng công thức chuyển trạng thái.

Mã code tương ứng như sau:

for i in range(size - 1, -1, -1):       # Duyệt qua các điểm bắt đầu của đoạn
    for j in range(i + 1, size):        # Duyệt qua các điểm kết thúc của đoạn
        # Tính toán giá trị tối ưu sau khi chuyển từ đoạn nhỏ sang đoạn lớn
        dp[i][j] = max(dp[i + 1][j - 1], dp[i + 1][j], dp[i][j - 1]) + cost[i][j]

1.2.3 Cách tiếp cận cơ bản cho loại bài toán thứ hai

Cách tiếp cận cơ bản cho bài toán Quy hoạch động trên đoạn chuyển từ nhiều đoạn nhỏ sang đoạn lớn là sử dụng công thức chuyển trạng thái sau: dp[i][j]=max/min{dp[i][k]+dp[k+1][j]+cost[i][j]},i<k≤jdp[i][j] = max / min \lbrace dp[i][k] + dp[k + 1][j] + cost[i][j] \rbrace, \quad i < k \le j.

  1. Trạng thái dp[i][j]dp[i][j] biểu thị giá trị lớn nhất / nhỏ nhất trên đoạn [i,j][i, j] (tức là tất cả các phần tử từ vị trí ii đến vị trí jj).
  2. cost[i][j]cost[i][j] biểu thị chi phí để kết hợp hai đoạn [i,k][i, k] và [k+1,j][k + 1, j] thành đoạn [i,j][i, j].
  3. max/minmax / min ở đây phụ thuộc vào việc bài toán yêu cầu tìm giá trị lớn nhất hay nhỏ nhất.

Cách tiếp cận cơ bản cho bài toán Quy hoạch động trên đoạn chuyển từ nhiều đoạn nhỏ sang đoạn lớn như sau:

  1. Duyệt qua các độ dài của đoạn.
  2. Duyệt qua các điểm bắt đầu của đoạn, dựa trên điểm bắt đầu và độ dài để tìm điểm kết thúc của đoạn.
  3. Duyệt qua các điểm chia của đoạn, tính toán giá trị tối ưu sau khi kết hợp các đoạn thành đoạn lớn bằng công thức chuyển trạng thái.

Mã code tương ứng như sau:

for l in range(1, n):               # Duyệt qua các độ dài của đoạn
    for i in range(n):              # Duyệt qua các điểm bắt đầu của đoạn
        j = i + l - 1               # Dựa trên điểm bắt đầu và độ dài để tìm điểm kết thúc của đoạn
        if j >= n:
            break
        dp[i][j] = float('-inf')    # Khởi tạo dp[i][j]
        for k in range(i, j + 1):   # Duyệt qua các điểm chia của đoạn
            # Tính toán giá trị tối ưu sau khi kết hợp các đoạn thành đoạn lớn
            dp[i][j] = max(dp[i][j], dp[i][k] + dp[k + 1][j] + cost[i][j])

2. Áp dụng của bài toán Quy hoạch động trên đoạn

Dưới đây, chúng ta sẽ trình bày cách tiếp cận cụ thể cho các bài toán Quy hoạch động trên đoạn dựa trên một số ví dụ.

2.1 Chuỗi con Palindrome dài nhất

2.1.1 Liên kết đề bài

2.1.2 Tóm tắt đề bài

Mô tả: Cho một chuỗi ss.

Yêu cầu: Tìm chuỗi con Palindrome dài nhất trong chuỗi ss và trả về độ dài của chuỗi con đó.

Giới hạn:

  • 1≤s.length≤10001 \le s.length \le 1000.
  • Chuỗi ss chỉ chứa các ký tự chữ cái thường.

Ví dụ:

  • Ví dụ 1:
Input: s = "bbbab"
Output: 4
Explanation: Một chuỗi con Palindrome dài nhất có thể là "bbbb".
  • Ví dụ 2:
Input: s = "cbbd"
Output: 2
Explanation: Một chuỗi con Palindrome dài nhất có thể là "bb".

2.1.3 Ý tưởng giải quyết

Ý tưởng 1: Quy hoạch động
1. Phân đoạn

Chia các đoạn dựa trên độ dài của đoạn.

2. Định nghĩa trạng thái

Định nghĩa trạng thái dp[i][j]dp[i][j] là độ dài chuỗi con Palindrome dài nhất trong đoạn [i,j][i, j] của chuỗi ss.

3. Công thức chuyển trạng thái

Chúng ta xét hai trường hợp cho các ký tự biên của đoạn [i,j][i, j]:

  1. Nếu s[i]=s[j]s[i] = s[j], thì dp[i][j]dp[i][j] sẽ bằng độ dài chuỗi con Palindrome dài nhất trong đoạn [i+1,j−1][i + 1, j - 1] cộng thêm 22, tức là dp[i][j]=dp[i+1][j−1]+2dp[i][j] = dp[i + 1][j - 1] + 2.
  2. Nếu s[i]≠s[j]s[i] \ne s[j], thì dp[i][j]dp[i][j] sẽ bằng giá trị lớn nhất giữa độ dài chuỗi con Palindrome dài nhất trong đoạn [i,j−1][i, j - 1] và độ dài chuỗi con Palindrome dài nhất trong đoạn [i+1,j][i + 1, j], tức là dp[i][j]=max(dp[i][j−1],dp[i+1][j])dp[i][j] = max(dp[i][j - 1], dp[i + 1][j]).

Vậy công thức chuyển trạng thái là:

dp[i][j]={dp[i+1][j−1]+2s[i]=s[j]max(dp[i][j−1],dp[i+1][j])s[i]≠s[j]dp[i][j] = \begin{cases} dp[i + 1][j - 1] + 2 & s[i] = s[j] \cr max(dp[i][j - 1], dp[i + 1][j]) & s[i] \ne s[j] \end{cases}

4. Điều kiện ban đầu
  • Độ dài của chuỗi con Palindrome duy nhất là 11, tức là dp[i][i]=1dp[i][i] = 1.
5. Kết quả cuối cùng

Vì dp[i][j]dp[i][j] phụ thuộc vào dp[i+1][j−1]dp[i + 1][j - 1], dp[i+1][j]dp[i + 1][j], dp[i][j−1]dp[i][j - 1], nên chúng ta nên duyệt theo thứ tự từ dưới lên, từ trái sang phải.

Dựa trên định nghĩa trạng thái, dp[i][j]dp[i][j] là độ dài chuỗi con Palindrome dài nhất trong đoạn [i,j][i, j] của chuỗi ss. Vậy kết quả cuối cùng là dp[0][size−1]dp[0][size - 1].

Ý tưởng 1: Code
class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        size = len(s)
        dp = [[0 for _ in range(size)] for _ in range(size)]
        for i in range(size):
            dp[i][i] = 1

        for i in range(size - 1, -1, -1):
            for j in range(i + 1, size):
                if s[i] == s[j]:
                    dp[i][j] = dp[i + 1][j - 1] + 2
                else:
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])

        return dp[0][size - 1]
Ý tưởng 1: Phân tích độ phức tạp
  • Độ phức tạp thời gian: O(n2)O(n^2), trong đó nn là độ dài của chuỗi ss.
  • Độ phức tạp không gian: O(n2)O(n^2).

2.2 Chọc bóng

2.2.1 Liên kết đến đề bài

2.2.2 Tóm tắt đề bài

Mô tả: Có nn quả bóng, được đánh số từ 00 đến n−1n - 1, mỗi quả bóng có một số trên đó và các số này được lưu trữ trong mảng numsnums. Bắt đầu từ việc chọc bóng. Khi chọc bóng thứ ii, bạn sẽ nhận được nums[i−1]×nums[i]×nums[i+1]nums[i - 1] \times nums[i] \times nums[i + 1] đồng tiền, trong đó i−1i - 1 và i+1i + 1 là số hiệu của hai quả bóng kề cạnh với quả bóng thứ ii. Nếu i−1i - 1 hoặc i+1i + 1 vượt quá ranh giới của mảng, thì giá trị của quả bóng đó được coi là 11.

Yêu cầu: Tìm số lượng đồng tiền tối đa có thể nhận được.

Giải thích:

  • Ví dụ 1:
Input: nums = [3,1,5,8]
Output: 167
Explanation:
nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins =  3*1*5    +   3*5*8   +  1*3*8  + 1*8*1 = 167
  • Ví dụ 2:
Input: nums = [1,5]
Output: 10
Explanation:
nums = [1,5] --> [5] --> []
coins = 1*1*5 +  1*5*1 = 10

2.2.3 Ý tưởng giải quyết

Ý tưởng 1: Quy hoạch động

Dựa vào yêu cầu đề bài, nếu i−1i - 1 hoặc i+1i + 1 vượt quá ranh giới của mảng, thì giá trị của quả bóng đó được coi là 11. Ta có thể thêm hai quả bóng ảo có giá trị 11 vào đầu và cuối mảng numsnums, từ đó ta có n+2n + 2 quả bóng và các số hiệu của chúng cũng được thay đổi thành 0∼n+10 \sim n + 1.

Vấn đề ban đầu đã được chuyển thành: Cho n+2n + 2 quả bóng, mỗi quả bóng có 11 số, đại diện cho số lượng đồng tiền trên quả bóng đó. Khi chọc bóng nums[i]nums[i], ta sẽ nhận được nums[i−1]×nums[i]×nums[i+1]nums[i - 1] \times nums[i] \times nums[i + 1] đồng tiền. Bây giờ ta cần chọc bóng tất cả các quả bóng từ 00 đến n+1n + 1 (không bao gồm quả bóng có số hiệu 00 và n+1n + 1), hỏi ta có thể nhận được tối đa bao nhiêu đồng tiền?

1. Phân đoạn

Phân đoạn theo độ dài của đoạn.

2. Định nghĩa trạng thái

Định nghĩa trạng thái dp[i][j]dp[i][j] là: Số lượng đồng tiền tối đa có thể nhận được khi chọc bóng từ quả bóng ii đến quả bóng jj (không bao gồm quả bóng ii và quả bóng jj).

3. Công thức trạng thái

Giả sử quả bóng cuối cùng được chọc trong đoạn từ ii đến jj có số hiệu là kk. Vậy dp[i][j]dp[i][j] phụ thuộc vào số lượng đồng tiền tối đa có thể nhận được từ hai đoạn (i,k)(i, k) và (k,j)(k, j) cộng với số lượng đồng tiền nhận được khi chọc quả bóng kk, tức là công thức trạng thái:

dp[i][j]=max{dp[i][k]+dp[k][j]+nums[i]×nums[k]×nums[j]},i<k<jdp[i][j] = max \lbrace dp[i][k] + dp[k][j] + nums[i] \times nums[k] \times nums[j] \rbrace, \quad i < k < j

4. Điểm khởi tạo
  • dp[i][j]dp[i][j] đại diện cho đoạn mở, nên i<j−1i < j - 1. Khi i≥j−1i \ge j - 1, số lượng đồng tiền tối đa có thể nhận được là 00, tức là dp[i][j]=0,i≥j−1dp[i][j] = 0, \quad i \ge j - 1.
5. Kết quả cuối cùng

Dựa vào định nghĩa trạng thái, dp[i][j]dp[i][j] đại diện cho số lượng đồng tiền tối đa có thể nhận được khi chọc bóng từ quả bóng ii đến quả bóng jj (không bao gồm quả bóng ii và quả bóng jj). Vậy kết quả cuối cùng là dp[0][n+1]dp[0][n + 1].

Ý tưởng 1: Code
class Solution:
    def maxCoins(self, nums: List[int]) -> int:
        size = len(nums)
        arr = [0 for _ in range(size + 2)]
        arr[0] = arr[size + 1] = 1
        for i in range(1, size + 1):
            arr[i] = nums[i - 1]
        
        dp = [[0 for _ in range(size + 2)] for _ in range(size + 2)]

        for l in range(3, size + 3):
            for i in range(0, size + 2):
                j = i + l - 1
                if j >= size + 2:
                    break
                for k in range(i + 1, j):
                    dp[i][j] = max(dp[i][j], dp[i][k] + dp[k][j] + arr[i] * arr[j] * arr[k])
        
        return dp[0][size + 1]
Ý tưởng 1: Phân tích độ phức tạp
  • Độ phức tạp thời gian: O(n3)O(n^3), trong đó nn là số lượng quả bóng.
  • Độ phức tạp không gian: O(n2)O(n^2).

2.3 Cắt cây gỗ với chi phí nhỏ nhất

2.3.1 Liên kết đến đề bài

2.3.2 Tóm tắt đề bài

Mô tả: Cho một cây gỗ có độ dài nn đơn vị, cây gỗ được đánh số từ 00 đến nn tại một số vị trí. Ví dụ, cây gỗ có độ dài 66 có thể được đánh số như sau:

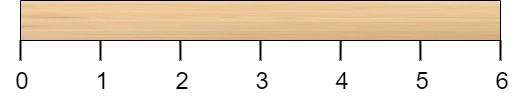
Cho một mảng số nguyên cutscuts, trong đó cuts[i]cuts[i] đại diện cho vị trí cần cắt cây gỗ.

Chúng ta có thể cắt cây gỗ theo thứ tự hoặc thay đổi thứ tự cắt.

Mỗi lần cắt, chi phí cắt là độ dài của cây gỗ cần cắt. Tổng chi phí cắt cây gỗ là tổng chi phí của tất cả các lần cắt. Khi cắt cây gỗ, cây gỗ sẽ được chia thành hai cây gỗ nhỏ hơn (tổng độ dài hai cây gỗ nhỏ bằng độ dài cây gỗ trước khi cắt).

Yêu cầu: Tìm tổng chi phí cắt cây gỗ nhỏ nhất.

Giải thích:

  • Ví dụ 1:
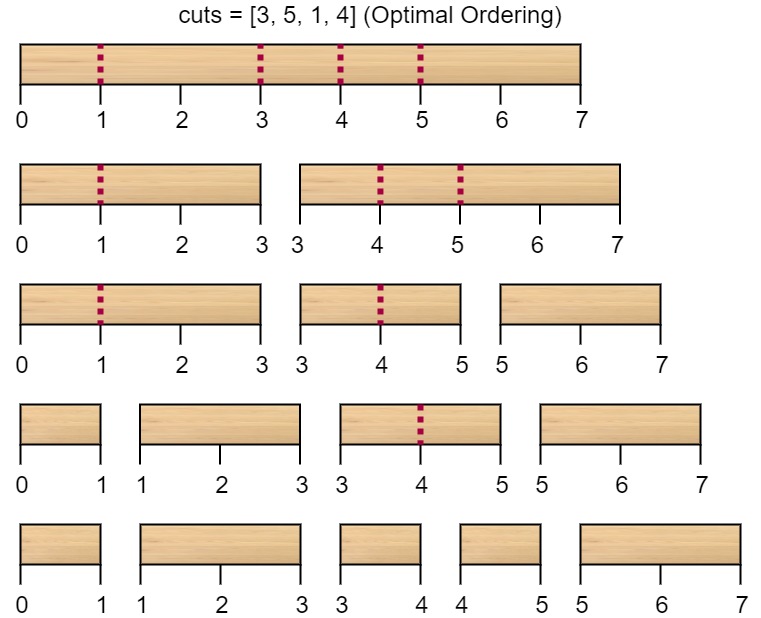
Input: n = 7, cuts = [1,3,4,5]
Output: 16
Explanation: Khi cắt theo thứ tự [1, 3, 4, 5], ta có các lần cắt như sau.
Lần cắt đầu tiên, chi phí cắt cây gỗ có độ dài 7 là 7. Lần cắt thứ hai, cây gỗ có độ dài 6 sau khi cắt lần đầu tiên, chi phí cắt là 6. Lần cắt thứ ba, cây gỗ có độ dài 4 sau khi cắt lần thứ hai, chi phí cắt là 4. Lần cắt cuối cùng, cây gỗ có độ dài 3 sau khi cắt lần thứ ba, chi phí cắt là 3. Tổng chi phí cắt là 7 + 6 + 4 + 3 = 20. Tuy nhiên, nếu thay đổi thứ tự cắt thành [3, 5, 1, 4], tổng chi phí cắt là 16 (như trong hình minh họa, 7 + 4 + 3 + 2 = 16).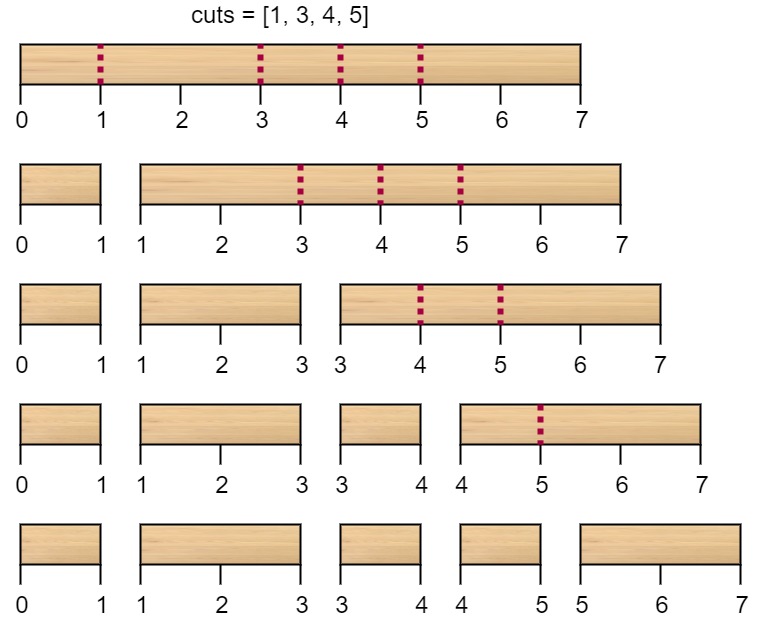
  • Ví dụ 2:
Input: n = 9, cuts = [5,6,1,4,2]
Output: 22
Explanation: Nếu cắt theo thứ tự cho trước, tổng chi phí cắt là 25. Tuy nhiên, có nhiều thứ tự cắt khác nhau có tổng chi phí cắt nhỏ hơn 25, ví dụ như [4, 6, 5, 2, 1] có tổng chi phí cắt là 22, là thứ tự cắt có tổng chi phí nhỏ nhất trong tất cả các thứ tự khả dụng.

2.3.3 Ý tưởng giải quyết

Ý tưởng 1: Quy hoạch động

Chúng ta có thể thêm vị trí 00 và vị trí nn vào mảng cutscuts, sau đó sắp xếp mảng cutscuts. Điều này sẽ tạo ra các "đoạn" liên tiếp trong mảng cutscuts tương ứng với các đoạn cần cắt trong cây gỗ.

1. Phân đoạn

Phân đoạn theo độ dài của đoạn.

2. Định nghĩa trạng thái

Định nghĩa trạng thái dp[i][j]dp[i][j] là: Chi phí cắt nhỏ nhất của cây gỗ trong đoạn [i,j][i, j].

3. Công thức trạng thái

Giả sử vị trí ii và vị trí jj là vị trí cắt cuối cùng trong đoạn, tức là dp[i][j]dp[i][j] phụ thuộc vào chi phí cắt nhỏ nhất của hai đoạn [i,k][i, k] và [k,j][k, j] cộng với chi phí cắt ở vị trí jj và ii.

Chi phí cắt ở vị trí jj và ii là độ dài của đoạn cây gỗ tương ứng, tức là cuts[j]−cuts[i]cuts[j] - cuts[i].

Công thức trạng thái: dp[i][j]=min{dp[i][k]+dp[k][j]+cuts[j]−cuts[i]},i<k<jdp[i][j] = min \lbrace dp[i][k] + dp[k][j] + cuts[j] - cuts[i] \rbrace, \quad i < k < j

4. Điểm khởi tạo
  • Các vị trí liền kề không cần cắt, chi phí cắt nhỏ nhất là 00, tức là dp[i−1][i]=0dp[i - 1][i] = 0.
  • Các vị trí khác mặc định là một giá trị rất lớn, tức là dp[i][j]=∞,i+1≠jdp[i][j] = \infty, \quad i + 1 \ne j.
5. Kết quả cuối cùng

Dựa vào định nghĩa trạng thái, dp[i][j]dp[i][j] đại diện cho chi phí cắt nhỏ nhất của cây gỗ trong đoạn [i,j][i, j]. Vậy kết quả cuối cùng là dp[0][size−1]dp[0][size - 1].

Ý tưởng 1: Code
class Solution:
    def minCost(self, n: int, cuts: List[int]) -> int:
        cuts.append(0)
        cuts.append(n)
        cuts.sort()
        
        size = len(cuts)
        dp = [[float('inf') for _ in range(size)] for _ in range(size)]
        for i in range(1, size):
            dp[i - 1][i] = 0

        for l in range(3, size + 1):        # Liệt kê độ dài đoạn
            for i in range(size):           # Liệt kê điểm bắt đầu đoạn
                j = i + l - 1               # Tính điểm kết thúc dựa trên điểm bắt đầu và độ dài
                if j >= size:      
                    continue
                dp[i][j] = float('inf')
                for k in range(i + 1, j):   # Liệt kê điểm chia đoạn
                    # Công thức trạng thái, tính giá trị tối ưu sau khi ghép đoạn
                    dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + cuts[j] - cuts[i])
        return dp[0][size - 1]
Ý tưởng 1: Phân tích độ phức tạp
  • Độ phức tạp thời gian: O(m3)O(m^3), trong đó mm là số lượng phần tử trong mảng cutscuts.
  • Độ phức tạp không gian: O(m2)O(m^2).
Made with ❤️ by Hung Nguyen
Copyright © 2016-2024 Hung Nguyen